算法优化---素数（质数）（Java版）

4.1优化算法-----输出素数

最简代码请直接移步文末

原代码：https://www.cnblogs.com/Tianhaoblog/p/15077840.html

对应优化如下

优化一：在遍历内循环时，只要满足一个“非1非自身”的数可以整除，直接break跳出循环，因为此时“i”已经不是质数。对“非质数”数据优化明显；

优化二：在遍历内循环时，判断“i”是否为质数，不用遍历2-->i，只要判断2-->根号i，若不能被整除，就说明“i”是质数。对所有数据均有优化，但因优化一存在，非质数已经跳出循环，所以此条优化更有助于“质数”的数据优化；



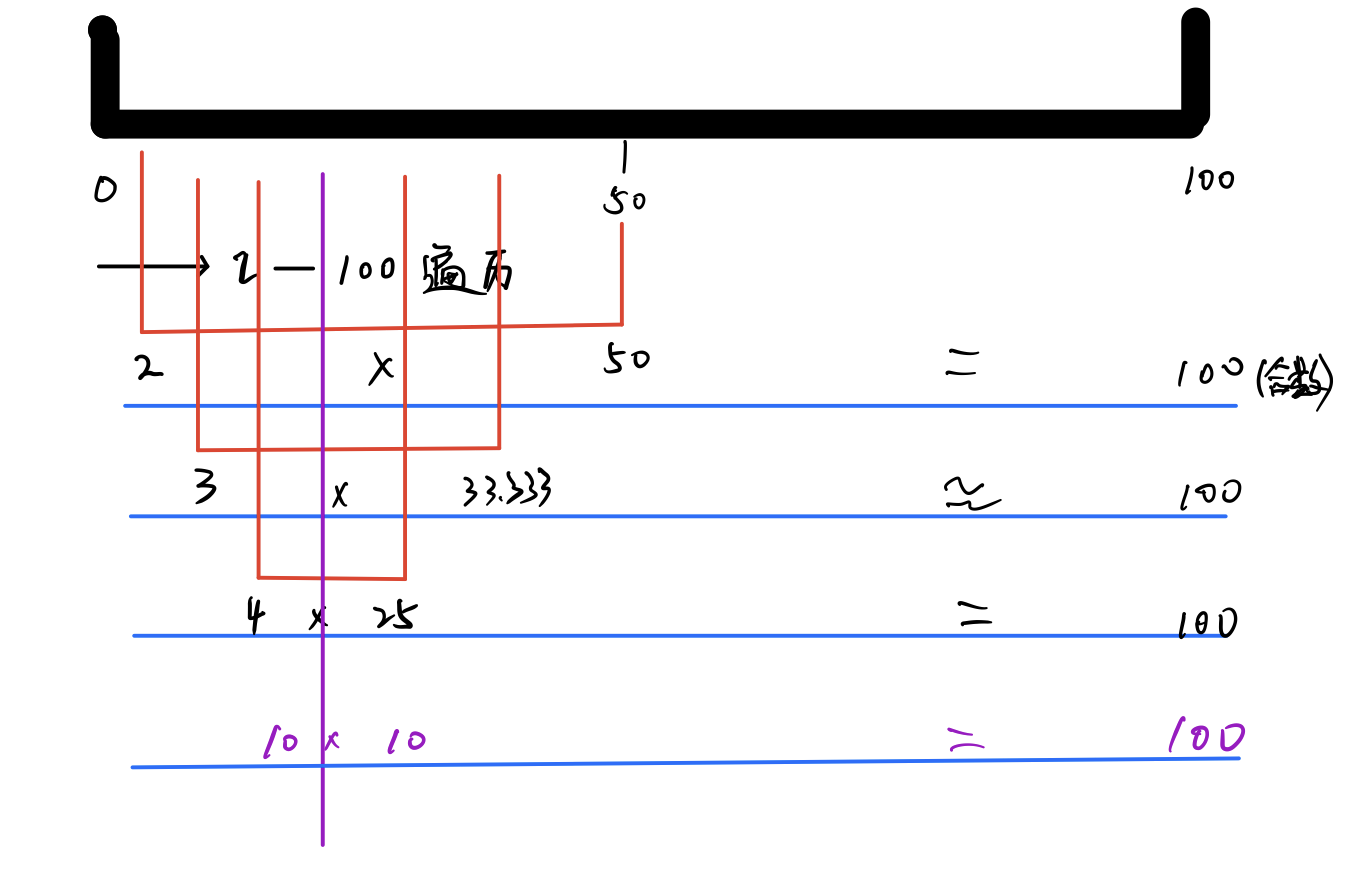
假设i=100,

判断是否在两数相乘等于第三个数

a × b = c

因为不包含1，所以 a 、b 两个数最小均为 2 ，且最大均为c / 2。

a = 2 时，b = c / 2，满足条件a × b = c；

a = c / 2 时，b = 2，满足条件a × b = c；

a 从 2 开始不断递增，到 c / 2截止（2，3，4，5，6，7————c / 2）

此时 b 从 c / 2 开始不断减小，到 2 截止（c / 2————7，6，5，4，3，2）

此时 a = 2 和 b = 2 时相当于重复遍历，找到 a 和 b 的临界点，停止遍历，这样就不会重复了，临界点就是 a = b 的点，如上述例子中的10，当 a = b 时，恰好 a 为根号c

代码如下：

public class PrimeNumber {
    public static void main(String[] args){
        long start = System.currentTimeMillis();//开始时间
        int isLine = 10;
        boolean isFlag = true;
        for (int i = 2; i <100000; i++) {//输出100000以内的素数
            for (int j = 2; j <= Math.sqrt(i); j++) {  //优化二：只取根号i ---对本身质数的数据优化！！！！
                if(i % j == 0){
                    isFlag = false;
                    break;//优化一：满足一个整除就跳出循环---对本身为非质数的数据优化！！！！！
                }
            }
            if(isFlag){
                System.out.print(i + " ");
                isLine--;
                if(isLine == 0){
                    System.out.println();
                    isLine = 10;
                }
            }else{
                isFlag = true;
            }
        }
        long end = System.currentTimeMillis();//结束时间
        System.out.println("程序运行时间：" + (end-start));//输出程序运行时间
    }
}

---

//输出100000以内的素数
2 3 5 7 11 13 17 19 23 29 //每行10个数据
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97 101 103 107 109 113
......//省略。。。
99761 99767 99787 99793 99809 99817 99823 99829 99833 99839
99859 99871 99877 99881 99901 99907 99923 99929 99961 99971
99989 99991
程序运行时间：136

最简版素数代码：

public class PrimeNumber {
    public static void main(String[] args){
        label:for (int i = 2; i <100000; i++) {
            for (int j = 2; j <= Math.sqrt(i); j++) {
                if (i % j == 0) {
                    continue label;//存在可以整除的数，跳出当前循环，回到外层循环继续执行。
                }
            }
            System.out.println(i);//因非质数已经通过continue跳出本层循环，凡是可以运行到此位置的，均为质数
        }
    }
}