Codeforces Round #236 (Div. 2)E. Strictly Positive Matrix(402E)

　　　　　　　　　　　　　　　　　　　　　　　　　　E. Strictly Positive Matrix

 

You have matrix a of size n × n. Let's number the rows of the matrix from 1 to n from top to bottom, let's number the columns from 1 ton from left to right. Let's use aij to represent the element on the intersection of the i-th row and the j-th column.

Matrix a meets the following two conditions:

• for any numbers i, j (1 ≤ i, j ≤ n) the following inequality holds: aij ≥ 0;
• .

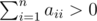Matrix b is strictly positive, if for any numbers i, j (1 ≤ i, j ≤ n) the inequality bij > 0 holds. You task is to determine if there is such integer k ≥ 1, that matrix ak is strictly positive.

Input

The first line contains integer n (2 ≤ n ≤ 2000) — the number of rows and columns in matrix a.

The next n lines contain the description of the rows of matrix a. The i-th line contains n non-negative integers ai1, ai2, ..., ain (0 ≤ aij ≤ 50). It is guaranteed that .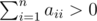

Output

If there is a positive integer k ≥ 1, such that matrix ak is strictly positive, print "YES" (without the quotes). Otherwise, print "NO" (without the quotes).

Sample test(s)

input

2
1 0
0 1

output

NO

input

5
4 5 6 1 2
1 2 3 4 5
6 4 1 2 4
1 1 1 1 1
4 4 4 4 4

output

YES

题意： 矩阵matrix[n][n], 对角线上元素不全为0， 其他元素的值大于等于0. 问是否存在k 使得 矩阵的k次幂之后 元素的值全部大于0.

设 A = B²  , B 为一邻接矩阵， 则A[i][j] 的实际意义为 从i到j 经过一个点（不包含i, j）的路径的个数。。。对于k次幂就是经过k-1个点的路径的个数了。

要使 A[i][j] 大于0 ，（有向图） i 到j必须连通。。 A[j][i] > 0 && A[i][j] < 0 ，则i, j之间必能形成回路。

可以理解为 从任意点开始都可以遍历整个有向图。

建两个图（正向 反向），分别跑dfs。。判断一下即可。

 #include <bits/stdc++.h>
 using namespace std;
 vector<int>G1[];
 vector<int>G2[];
 int  c1, c2;
 bool vis[];
 void dfs1(int r)
 {
     c1++;
     vis[r] = true;
     for (int i = ; i < G1[r].size(); i++)
     {
         if (!vis[G1[r][i]])
             dfs1(G1[r][i]);
     }
 }
 void dfs2(int r)
 {
     c2++;
     vis[r] = true;
     for (int i = ; i < G2[r].size(); i++)
     {
         if (!vis[G2[r][i]])
             dfs2(G2[r][i]);
     }
 }
 int main()
 {
     #ifndef ONLINE_JUDGE
         freopen("in.txt","r",stdin);
     #endif
     int n;
     while (~scanf ("%d", &n))
     {
         for (int i = ; i <= n; i++)
         {
             G1[i].clear();
             G2[i].clear();
         }
         for (int i = ; i < n; i++)
         {
             for (int j = ; j < n; j++)
             {
                 int x;
                 scanf ("%d", &x);
                 if (i != j && x)
                 {
                     G1[i+].push_back(j+);
                     G2[j+].push_back(i+);
                 }
             }
         }
         c1 = c2 = ;
         memset(vis, false, sizeof(vis));
         dfs1();
         memset(vis, false, sizeof(vis));
         dfs2();
         printf("%s\n", (c1 == n && c2 == n) ? "YES" : "NO");
     }
     return ;
 }