leetcode62

使用排列组合计算公式来计算，注意使用long long型数据保证计算不会溢出。

 class Solution {
 public:
     long long FA(long long a) //定义阶乘函数FA
     {
         long long x = ;//定义变量b
         for (int i = ; i <= a; i++)//计算阶乘
             x *= i;
         return x;//返回值得到b=a！
     }

     long long FA(long long a, long long b) //定义阶乘函数FA
     {
         //long long b = 1;//定义变量b
         long long x = ;
         for (int i = b; i <= a; i++)//计算阶乘
             x *= i;
         return x;//返回值得到b=a！
     }

     int uniquePaths(int m, int n) {
         long long a = FA(m -  + n - , max(m, n));
         long long b = FA(min(m, n) - );
         return (int)(a / b);
     }
 };

补充一个使用dp的方案，python 实现：

 class Solution:
     def uniquePaths(self, m: 'int', n: 'int') -> 'int':
         dp =[[0 for col in range(n)] for row in range(m)]
         for i in range(m):
             dp[i][0] =  1

         for j in range(n):
             dp[0][j] = 1
         print(dp)
         for i in range(1,m):
             for j in range(1,n):
                 dp[i][j] = dp[i-1][j] + dp[i][j-1]
         return dp[m-1][n-1]

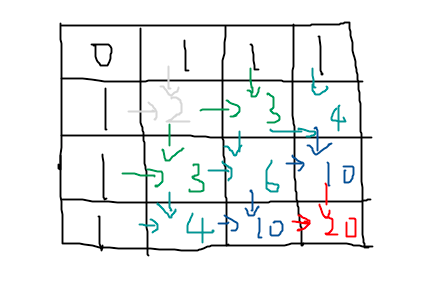
初始化index==0的行和index==0的列，起点为0，其他都是1（黑色）。

然后从(1,1)开始计算，可以一行一行的计算，也可以一列一列的计算，也可以按对角线计算，总之一步一步的推进，一直计算到(i,j)元素（红色），即为所求。

注意，dp[i][j]==dp[m-1][n-1]。