6-10 SVM支持向量机1

都是特征加上分类器。还将为大家介绍如何对这个数据进行训练。如何训练得到这样一组数据。

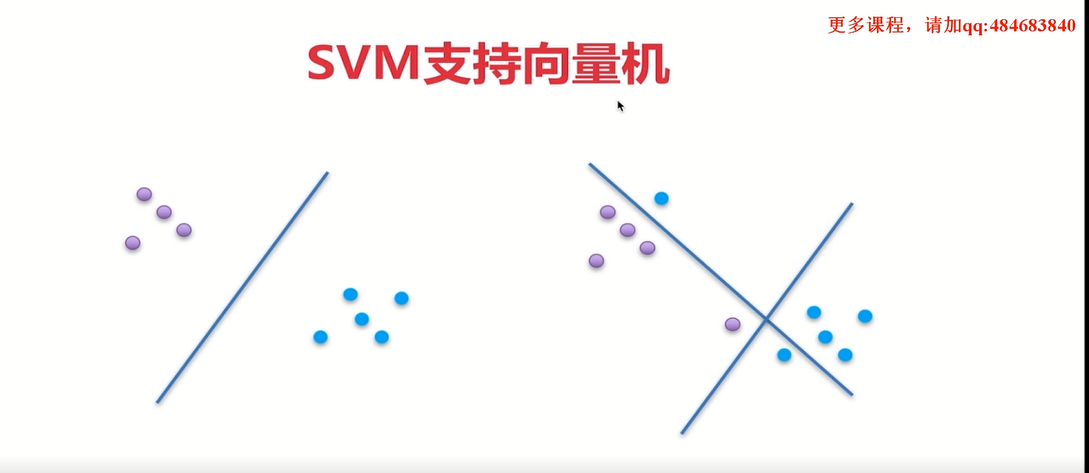
其实SVM支持向量机，它的本质仍然是一个分类器。既然是一个分类器，它就具有分类的功能。我们可以使用一条直线来完成分类，这是一种比较简单的情况。

这是在我们的二维平面上。二维平面上它是由直线和多个直线来组成。如果我们把当前的左边的这样一个图和右边的这样一个图，我们把它投影到一个高维空间上，实际上它就是一个超平面。

这就是SVM支持向量机的核心。首先它的本质它是一个分类器。这个分类器如何进行分类呢？它就是寻求一个最优的超平面来完成这样一个分类。

在寻求超平面的时候它有多种方式。可以使用若干条直线，也可以使用若干个曲线等等。

可以看到一个最简单的SVM分类器是如何进行训练的。

在进行SVM训练的时候，有一个对数据最基本的要求：所有的数据都必须要有标签label。标签是描述当前一组数据唯一的一个属性。我们当前的数据是男生的身高和体重和女生的身高和体重，所以这个标签描述的就是当前的这一个数据到底是男生还是女生。所以每一个身高和体重都要有一个唯一的标签来进行对应。

组装完之后每一个数据都对应的label中的一个标签，然后我们才可以进行训练。像这一种标签的训练我们把它交托为监督学习。监督学习其实最本质的含义，就是在学习的过程中，每学习一组数据就要告诉它学习得对还是不对。

# svm本质 寻求一个最优的超平面 分类
# svm 核: line
# 身高体重 训练 预测
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 1 准备data 男生的身高体重 女生的身高体重
rand1 = np.array([155,48],[159,50],[164,53],[168,56],[172,60])#女生的五组数据,五组数据中分别描述五组人不同的身高和体重
rand2 = np.array([152,53],[156,55],[160,56],[172,64],[176,65])

# 2 label 标签
label = np.array([0],[0],[0],[0],[0],[1],[1],[1],[1],[1])

# 3 data 对数据进行一定的处理,特别是我们的训练数据.我们的训练数据要这样来做.
data = np.vstack((rand1,rand2))#给它一个元组,合并rand1和rand2
data = np.array(data,dtype='float32')

# svm 所有的数据都要有label
# [155,48] -- 0 女生 [152,53] ---1 男生
# 监督学习