python堆排序

堆是完全二叉树

子树是不相交的

度 节点拥有子树的个数

满二叉树：

每个节点上都有子节点（除了叶子节点）

完全二叉树：

叶子结点在倒数第一层和第二层，最下层的叶子结点集中在树的左部

，在右边的话，左子树不能为空

二叉搜索树：

左边子节点小于父节点，右边子节点大于父节点

堆：

也叫队列，在堆尾插入，在堆头取出

最大堆：

最上边比下边的两个数都大，所有的节点都满足这个规则

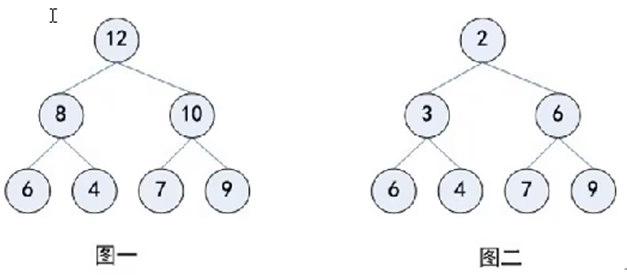
最小堆：

父节点一定比两个子节点要小

特征：

堆起始坐标从1开始

如果用列表表示一个堆：

堆的坐标从1开始算

当前坐标是i

左节点坐标是2i

右节点坐标是2i+1

父节点坐标是i//2 取整

如果想找到最后一个带有子节点的节点坐标：

堆的长度//2

[0,1,2,3,4,5]

[0,1,2,3,4,5,6,7]

1

2  2*1+1=3

2*2  2*2+1=5

0

1        2

3    4    5   6

堆的坐标从0开始算

当前坐标是i

左节点坐标是2i+1

右节点坐标是2i+2

父节点坐标是(i-1)//2 取整

如果想找到最后一个带有子节点的节点：

(堆的长度-1)//2

父节点的位置是K//2,它的左节点是2k，右节点是2k+1

在堆里插入一个元素：上滤

最大堆：

所有的父节点必须大于它的两个子节点

如果将新元素增加到堆的末尾：加一个88

要保证最大堆的规则，新元素和父节点调整交换的操作叫做上滤

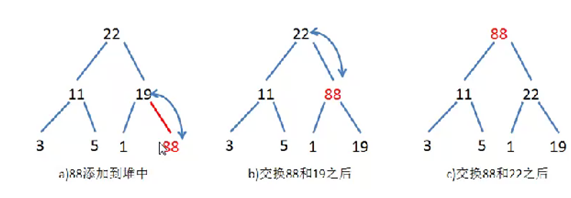
只要插入的节点比父节点小，就不做交换了，不交换那么排序就停止了

当发生了新插入节点和父节点没有交换的情况，那么上滤过程及结束了

删除根元素：下滤

删除堆顶元素，两个子元素比较，大的上去，空出的元素的两个子元素继续比较，大的再上去。。。

最小堆：

所有的父节点必须小于它的两个子节点

堆排序：

算法：一个列表是待排序的

构造最大（小）堆：

最大堆的规则：堆中所有的父节点必须都大于它的子节点

最大堆中的最大值是：根

最小堆的规则：堆中所有的父节点必须都小于它的子节点

最小堆中最小值是：根

排序：

假设使用最大堆

1生成一个空列表存储排序后的结果

2将待排序的list构造成最大堆

3将最大堆的根元素放到空列表中，将剩余的元素通过下滤重新构造最大堆

4然后重复3的步骤，知道所有的元素都当过一次最大堆

拆解过程：

列表中的元素是排好序的，并且是降序的

result =[]

5

3    4

1  2

第一次：result:[5]

3    4

1  2

剩下的元素要构造新的最大堆

4

3

1  2

第二次：result:[5，4]

3

1  2

再次构造最大堆

第三次：result:[5，4，3]

1 2

再次构造最大堆

2

1

第三次：result:[5，4，3 ,2]

1

再次构造最大堆

第四次：result:[5，4，3,2，1]

完成了所有元素当过一次堆的根元素条件，结束堆排序

构造最大堆的时候，如何构造：

从堆的最下层开始构造，每构造一次进行一次上滤

将最大值向上传递。

下滤是从堆顶取值

代码：

# encoding=utf-8

#左叶子、右叶子和父节点，三个元素，找到最大的一个

def maxHeap(heap,heapSize,i):#构造最大堆

#参数heap为一个list，heapsize是指定这个list要操作的长度

#i为某个节点，假设我们传递的是列表的倒数第三个元素

#它的左节点坐标：2i

#那么它的右节点坐标：2i + 1

#它的父节点：i/2

left = 2*i +1

right = 2*i +2

larger = i#当前节点的值

#通过2次if的比较，将left、right和larger三者的最大值找到

#然后将最大值所在的坐标赋值给larger

if left < heapSize and heap[larger] < heap[left]:

larger = left

if right < heapSize and heap[larger] < heap[right]:

larger = right

#以上两步是把三个节点中，最大的值的坐标给了larger

#如果lager的值不是i，说明i的值需要和最大值进行交换

#因为i的坐标是最大堆的堆顶，所以必须是最大值

#如果不是i最大，则说明左结点，或者右节点最大，交换值

#后，说明下面的堆有可能需要进行调整，所以通过递归来

#建立左（右）结点下的最大堆。

#如果最大值就是i，没有进行交换值，所以不需要进行建立

#左（右）结点下的最大堆，这是因为

#做交换，如果最大值的坐标不是当前节点的坐标，说明更大的是左右节点之一

#就把最大那个和当前节点做一个交换，这样最大的就跑到上边去了

if larger != i:

heap[i],heap[larger] = heap[larger],heap[i]

maxHeap(heap,heapSize,larger)#递归调用larger是左节点坐标或者右节点坐标，继续去找下边的最大值，做交换

#如果发生了larger =i 的情况，则次函数调用结束

#以上步骤完成，堆顶坐标为i坐标的最大子堆建立好了

def buildMaxHeap(heap):

#heap参数是未排序、未建堆的list

heapSize = len(heap)

#堆的长度//2可以找到堆里面的

#最后一个带有子节点的节点

#循环可以实现从堆的最下层节点开始建堆

#每次建立的堆都是一个最大堆

#简单来说把所有字段都建成最大堆

#然后组成了最终的最大堆

for i in range((heapSize-1)//2 -1,-1,-1):

maxHeap(heap,heapSize,i)

#(heapSize-1)//2是算出来当前堆中最后一个含有子节点的坐标

'''

5

3      4

2   1  -1

'''

def heapSort(heap):

#先把所有元素先建立一个最大堆

buildMaxHeap(heap)

#将堆中所有的元素都遍历一遍

#让每个元素都做一次堆顶

#然后将堆顶的每个元素都换到堆的最后一个节点

for i in range(len(heap)-1,-1,-1):

heap[0],heap[i] = heap[i],heap[0]

#maxheap中的i是列表的长度，这样可以防止追加到

#堆后面的元素重新被当做最大堆元素进行建队

maxHeap(heap,i,0)

return heap

#第一次循环的时候，把最大值放到了列表最后面

#把最后一个值（肯定不是最大值）放到了堆顶，然后把不包含最后一个元素的

#剩余元素，重新进行最大堆排序

#第二次循环的时候，把堆顶（次大值）放到列表倒数的第二个位置，然后把不包含最后

#两个元素的剩余元素，重新进行建立最大堆

#。。。。

#循环结束，那么列表的数据就排好了

if __name__ == '__main__':

heap1 = [3,4,5,6,23,4,1,1,23,45,6678]

print (heap1)

heapSort(heap1)

print (heap1)

算法：

将一个未排序的list,做成最大堆

buildMaxHeap函数通过maxHeap函数构造了最大堆

第一次从最大堆取出的元素和列表的最后一个的元素交换

位置，我们就找到了最大值

剩余的元素，进行新的最大堆建立

第二次从新建的最大堆堆顶取出来最大值，这个值和

列表中的倒数第二个数进行交换，那么第二大的值就找到了，

此时，最大值在列表的最后，第二大值在列表的倒数

第二个元素

第三次。。。。。重复上面的过程

直到所有的元素都被交换过一次位置

刚才有一个地方讲解有偏差

maxHeap 这个函数的交换逻辑，应该是既不算上滤，也不算下滤

上滤：新插入元素和父节点比对，发生交换。下滤：左右节点比对后发生交换

maxHeap 这个函数的交换逻辑是三个数找到最大的，和上滤下滤还是有一些区别。

for i in range((heapSize-1)//2,-1,-1):
        maxHeap(heap,heapSize,i) 
这个循环要理解一下：

这个循环调用，表示从最下层的子树，开始实现最大堆，这个就是我刚才说的从最下层开始建立最大堆的过程