[ARC062F]Painting Graphs with AtCoDeer

题意：一个无向图，用$k$种不同的颜色给每条边染色，问能染出多少种不同的图，如果两张图能通过循环移位环边使得颜色相同，那么这两张图被认为是相同的

数学太差伤不起啊...补了一下Burnside定理的证明，这里写一些类似笔记的东西...

置换$\left(\begin{matrix}1\cdots n\\i_1\cdots i_n\end{matrix}\right)$有合成运算$\circ$，满足结合律，有单位元$\iota$，存在唯一逆元满足$f\circ f^{-1}=\iota$，所有$n!$个置换构成集合$S_n$

如果$G\subseteq S_n$且满足以下三条性质，定义它为置换群

1.$\forall f,g\in G,f\circ g\in G$

2.$\iota\in G$

3.$\forall f\in G,f^{-1}\in G$

每一个置换群都满足消去律$f\circ g=f\circ h\Rightarrow g=h$

$\rho_n=\left(\begin{matrix}1&\cdots&n-1&n\\2&\cdots&n&1\end{matrix}\right)$，易证$C_n=\{\rho_n^i|1\leq i\leq n\}$是一个置换群

着色$\mathbf c$：$i$的颜色为$c(i)$，着色集合$\mathcal C$

定义$f*\mathbf c$为使$i_k$的颜色为$c(k)$的着色（就是把颜色沿着置换移动）

$\forall f\in G,\mathbf c\in\mathcal C,f*\mathbf c\in\mathcal C$

$(g\circ f)*\mathbf c=g*(f*\mathbf c)$

若$\mathbf c_1,\mathbf c_2\in\mathcal C$，$\exists f\in G$使$f*\mathbf c_1=\mathbf c_2$，称$\mathbf c_1$等价于$\mathbf c_2$，记作$\mathbf c_1\sim\mathbf c_2$，这是$\mathcal C$上的等价关系

$\mathbf c$的稳定核$G(\mathbf c)=\{f|f\in G,f*\mathbf c=\mathbf c\}$是置换群

$\mathcal C(f)=\{\mathbf c|\mathbf c\in\mathcal C,f*\mathbf c=\mathbf c\}$

快要证Burnside定理了，先做一些准备工作

1.$\forall f,g\in G,f*\mathbf c=g*\mathbf c\Leftrightarrow f^{-1}\circ g\in G(\mathbf c)$

正：$(f^{-1}\circ g)*\mathbf c=f^{-1}*(g*\mathbf c)=f^{-1}*(f*\mathbf c)=\mathbf c\Rightarrow f^{-1}\circ g\in G(\mathbf c)$

反：$\mathbf c=(f^{-1}\circ g)*\mathbf c=f^{-1}*(g*\mathbf c)\Rightarrow f*\mathbf c=g*\mathbf c$

2.与$\mathbf c$等价的着色数$\left|\{f*\mathbf c|f\in G\}\right|=\dfrac{|G|}{|G(\mathbf c)|}$

由1得$f*\mathbf c=g*\mathbf c\Rightarrow g\in\{{f\circ h}|h\in G(\mathbf c)\}$，由消去律得$f\circ h=f\circ h'\Rightarrow h=h'$，所以对每个$f$恰有$|G(\mathbf c)|$个满足要求的$g$，得证

现在来证Burnside定理：非等价着色数$N(G,\mathcal C)=\dfrac1{|G|}\sum\limits_{f\in G}|\mathcal C(f)|$

先用两种方式计数满足$f*\mathbf c=\mathbf c$的$(f,\mathbf c)$的对数

$\sum\limits_{f\in G}|\mathcal C(f)|=\sum\limits_{\mathbf c\in\mathcal C}|G(\mathbf c)|$

由2得$\sum\limits_{\mathbf c\in\mathcal C}|G(\mathbf c)|=|G|\sum\limits_{\mathbf c\in\mathcal C}\dfrac1{(与\mathbf c等价的着色数)}$

右边的sigma中，每个等价类都贡献$1$，所以它等于$N(G,\mathcal C)$，定理得证

在此题中，如果一个点双只含一个环，就要用Burnside定理计数方案

设它有$n$条边，这题的循环移位对应置换群$C_n$

$|\mathcal C(\rho_n^i)|=k^{(n,i)}$，这是因为如果$\rho_n^i*\mathbf c=\mathbf c$那么$c(p)=c(p+i)$，这个限制把$n$条边分成了互相独立的$(n,i)$组，每组必须同色

所以方案数是$\dfrac1n\sum\limits_{i=1}^nk^{(i,n)}$

如果一个点双含多个环，那么我们有办法交换任意两边

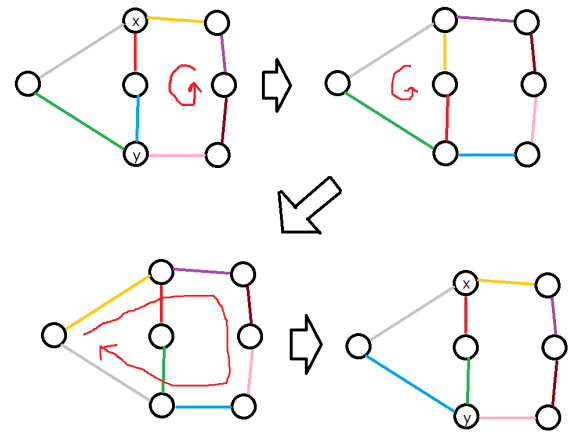
题解上的这张图告诉我们，一个度数$\geq3$的点的两条出边可以被交换（图中的绿和蓝）

然后我们可以交换任意相邻边，先把它们转到度数$\geq3$的点，做如上变换，再转回去即可

然后我们可以交换任意两边，用至多两次操作我们可以使它们相邻，交换后倒着操作回去即可

所以这样的点双方案数只与颜色数有关，$n$条边的点双答案为$\binom{n+k-1}{k-1}$

不属于任何点双的边对答案的贡献就是$k$了

#include<stdio.h>
#include<vector>
#include<set>
using namespace std;
typedef long long ll;
const int mod=1000000007;
int mul(int a,int b){return a*(ll)b%mod;}
void inc(int&a,int b){(a+=b)%=mod;}
int pow(int a,int b){
	int s=1;
	while(b){
		if(b&1)s=mul(s,a);
		a=mul(a,a);
		b>>=1;
	}
	return s;
}
vector<int>g[60];
int fac[210],rfac[210],k;
int C(int n,int k){return mul(fac[n],mul(rfac[k],rfac[n-k]));}
int dfn[60],low[60],stk[60],tp,M,ans;
set<int>s;
int gcd(int a,int b){return a%b==0?b:gcd(b,a%b);}
int burnside(int n){
	int i,s=0;
	for(i=1;i<=n;i++)inc(s,pow(k,gcd(i,n)));
	return mul(s,pow(n,mod-2));
}
void dfs(int x){
	int t,n,m;
	dfn[x]=low[x]=++M;
	stk[++tp]=x;
	for(int y:g[x]){
		if(!dfn[y]){
			dfs(y);
			low[x]=min(low[x],low[y]);
			if(low[y]>=dfn[x]){
				s.clear();
				do{
					t=stk[tp--];
					s.insert(t);
				}while(t!=y);
				s.insert(x);
				n=s.size();
				m=0;
				for(int x:s){
					for(int y:g[x]){
						if(s.count(y))m++;
					}
				}
				m>>=1;
				if(m<n)ans=mul(ans,k);
				if(n==m)ans=mul(ans,burnside(m));
				if(n<m)ans=mul(ans,C(m+k-1,k-1));
			}
		}else
			low[x]=min(low[x],dfn[y]);
	}
}
int main(){
	int n,m,i,x,y;
	scanf("%d%d%d",&n,&m,&k);
	for(i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		g[x].push_back(y);
		g[y].push_back(x);
	}
	fac[0]=1;
	for(i=1;i<=m+k;i++)fac[i]=mul(fac[i-1],i);
	rfac[m+k]=pow(fac[m+k],mod-2);
	for(i=m+k;i>0;i--)rfac[i-1]=mul(rfac[i],i);
	ans=1;
	for(i=1;i<=n;i++){
		if(!dfn[i])dfs(i);
	}
	printf("%d",ans);
}