20145240 GDB调试汇编堆栈过程分析

20145240 GDB调试汇编堆栈过程分析

测试代码

#include<stdio.h>

short addend1 = 1;
static int addend2 = 2;
const static long addend3 = 3;

static int g(int x)
{
	return x + addend1;
}  

static const int f(int x)
{
	return g(x + addend2);
}

int main(void)
{
	return f(8) + addend3;
}

分析过程

• 需要使用sudo apt-get install libc6-dev-i386命令安装一个库之后就可以产生汇编代码了。

• 输入gcc -g example.c -o example -m32指令在64位机器上产生32位汇编

• 然后使用gdb example指令进入gdb调试器

• 通过命令b example.c:main在main函数设置一个断点

• run启动程序，发现断点已经设置好了，在19行

• disassemble获取汇编代码，若命令不带参数，默认的反汇编范围是所选择帧的pc附近的函数

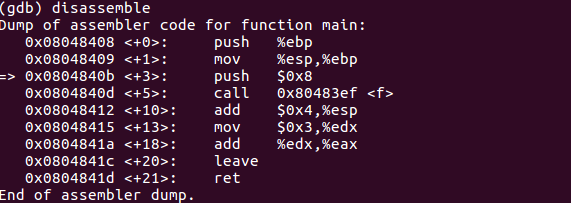
• 输入info registers列出使用的寄存器的值

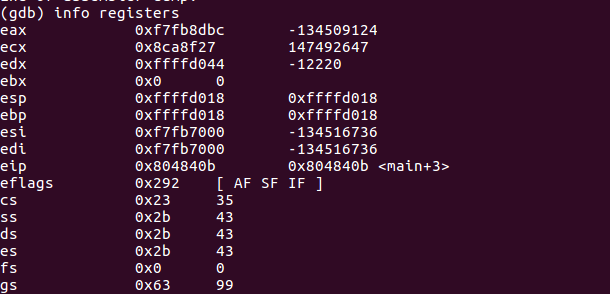
• 可见此时主函数的栈基址为0xffffd018，用x 0xffffd018指令查看内存地址中的值,堆栈内容皆为0

• 结合display命令和寄存器或pc内部变量，做如下设置：display /i $pc，这样在每次执行下一条汇编语句时，都会显示出当前执行的语句， $pc 代表当前汇编指令，/i 表示以十六进行显示。

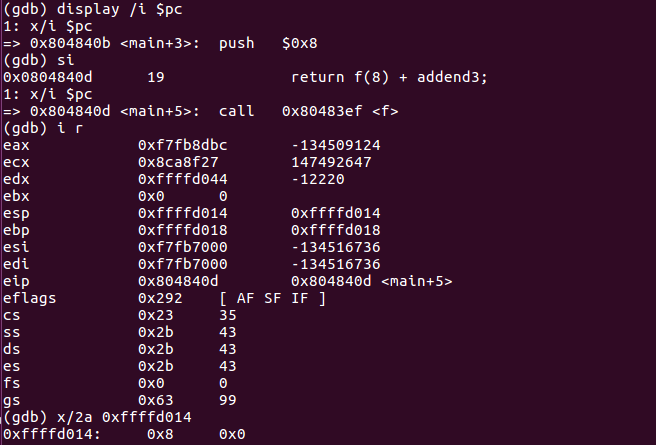
使用以上三个指令，观察其变化

• call将下一条指令的所在地址（即当时程序计数器PC的内容）入栈

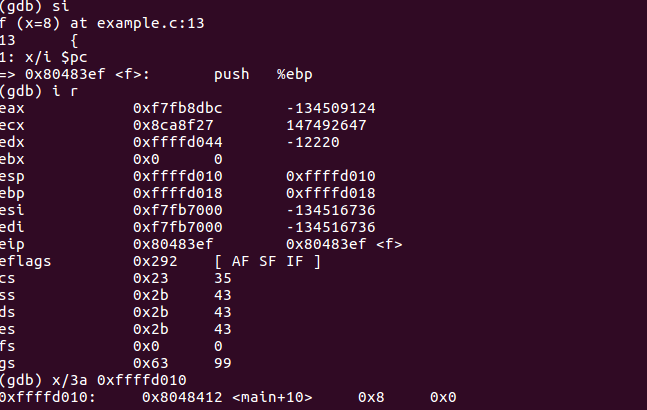
• 将上一个函数的基址入栈，将当前%esp作为新基址。

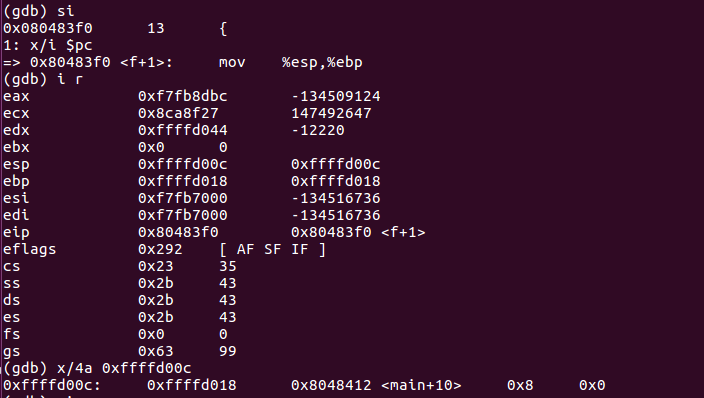
• 准备传参

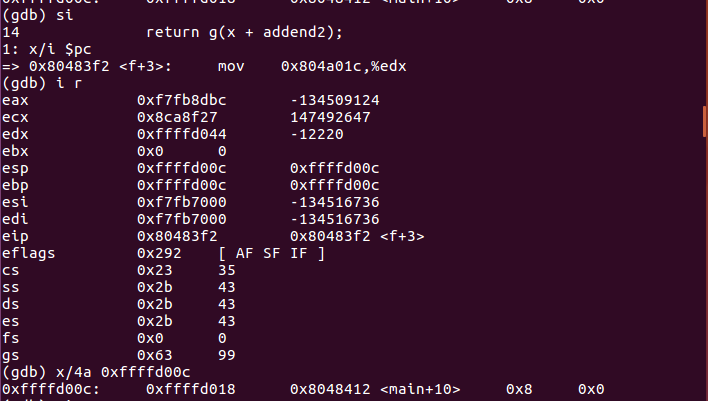
• 计算在%eax中进行

• 查看f函数的汇编代码

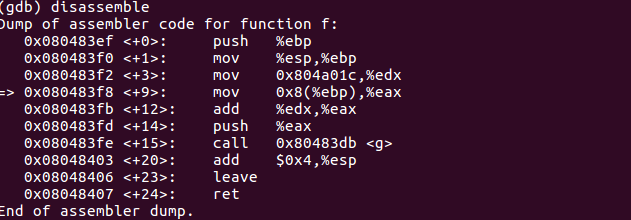
• 实参入栈

• call指令将下一条指令的地址入栈

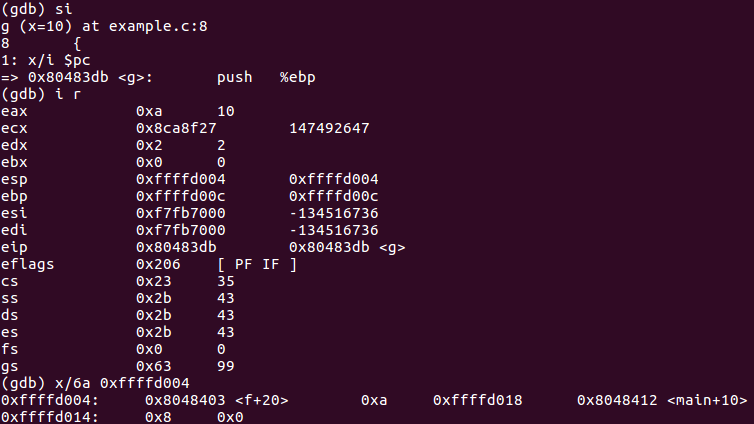
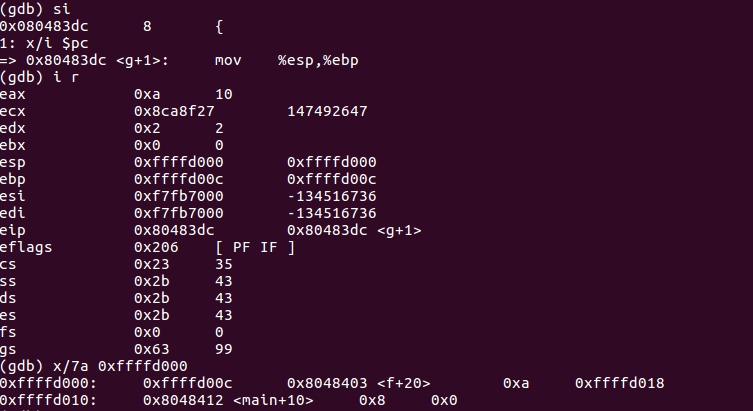
• 计算short+in

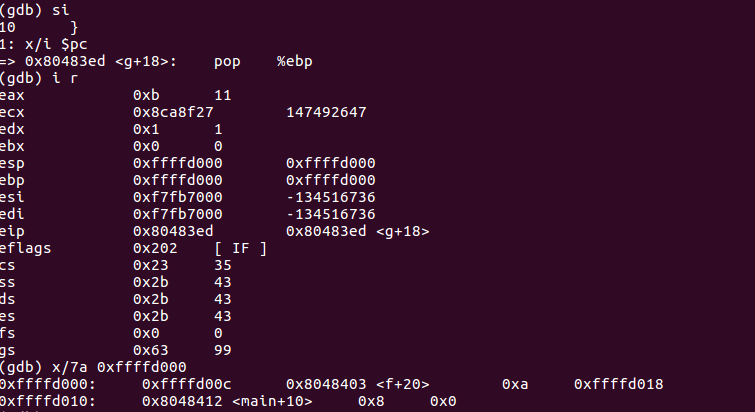
• pop %ebp指令将栈顶弹到%ebp中

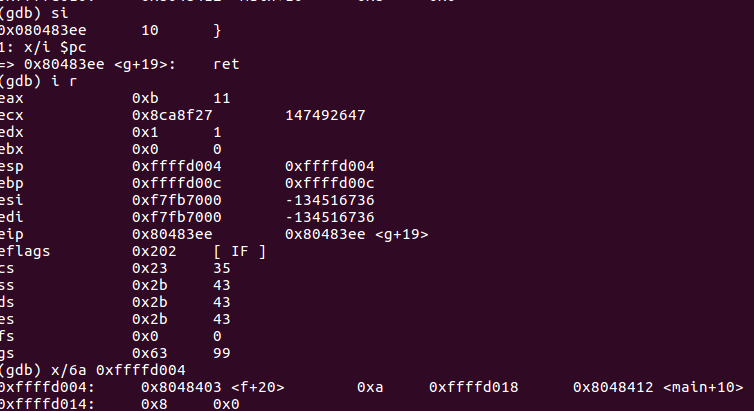
• ret指令将栈顶弹给%eip

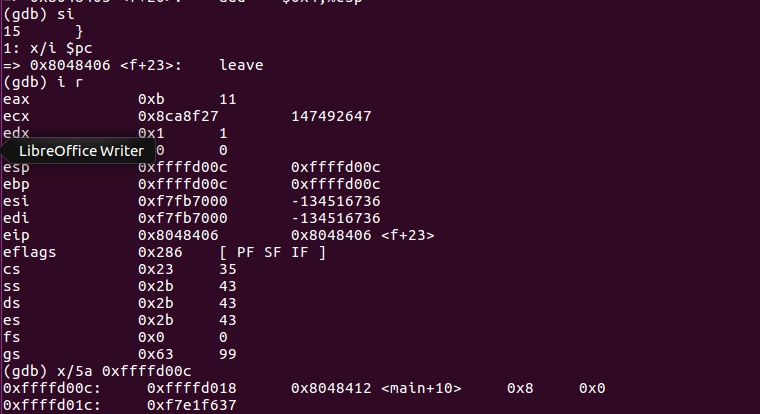
• 因为函数f修改了%esp，所以用leave指令恢复。leave指令先将%esp对其到%ebp，然后把栈顶弹给%ebp，释放当前子程序在堆栈中的局部变量,恢复被函数修改的%ebp和%esp

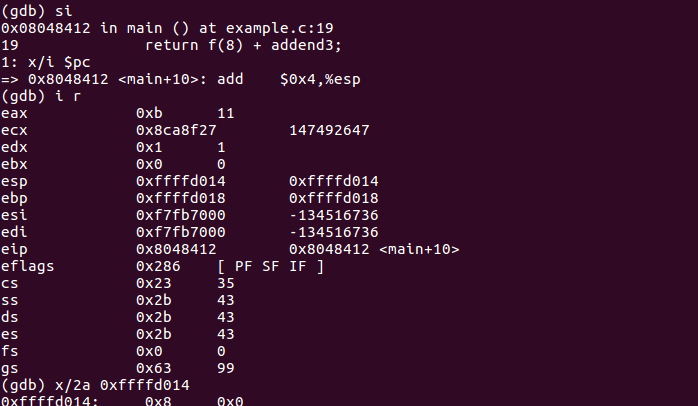
• 主函数汇编代码

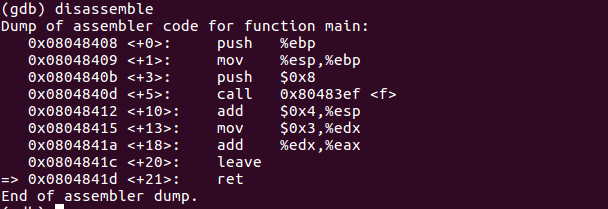
• 将%edx于%eax相加

• leave返回准备栈

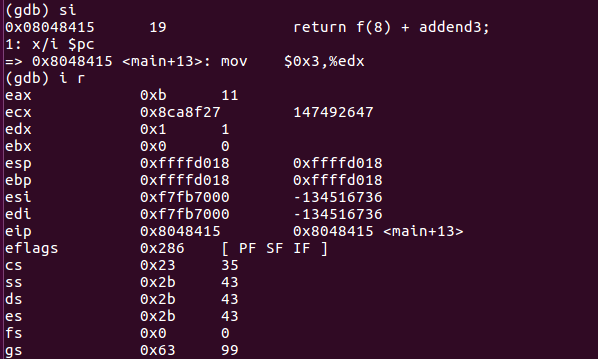
• ret结束main函数

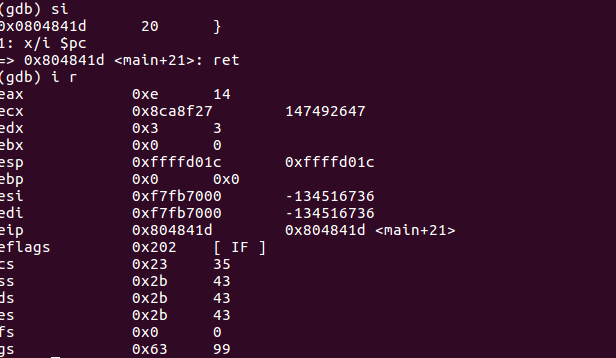
指令	%esp	%ebp	堆栈
push $0x8	0xffffd018	0xffffd018	0x0
call 0x80483ef	0xffffd014	0xffffd018	0x8 0x0
push %ebp	0xffffd010	0xffffd018	0x8048412 0x8 0x0
mov %esp,%ebp	0xffffd00c	0xffffd018	0xffffd018 0x8048412 0x8 0x0
mov 0x804a01c,%edx	0xffffd00c	0xffffd00c	0xffffd018 0x8048412 0x8 0x0
call 0x80483db	0xffffd008	0xffffd00c	0xa 0xffffd018 0x8048412 0x8 0x0
push %ebp	0xffffd004	0xffffd00c	0x8048403 0xa 0xffffd018 0x8048412 0x8 0x0
mov %esp,%ebp	0xffffd000	0xffffd00c	0xffffd00c 0x8048403 0xa 0xffffd018 0x8048412 0x8 0x0
movzwl 0x804a018,%eax	0xffffd000	0xffffd000	0xffffd00c 0x8048403 0xa 0xffffd018 0x8048412 0x8 0x0
ret	0xffffd004	0xffffd00c	0x8048403 0xa 0xffffd018 0x8048412 0x8 0x0
leave	0xffffd00c	0xffffd00c	0xffffd018 0x8048412 0x8 0x0
ret	0xffffd010	0xffffd018	0x8048412 0x8 0x0
add $0x4,%esp	0xffffd014	0xffffd018	0x8 0x0
mov $0x3,%edx	0xffffd018	0xffffd018	0x0
ret	0xffffd01c	0x0