区间重叠计算及IntervalTree初识

最近被人问到这样一个问题的解决方案：在一个餐馆的预定系统中，接受用户在未来任意一段时间内的预订用餐，用户在预订的时候需要提供用餐的开始时间和结束，餐馆的餐桌是用限的，问题是，系统要在最快的时间段计算出在该用户预定的时间段内是否还有可用的餐桌？其实类似的问题我们在做系统时经常碰到，比如在一个“任务管理”系统中，我们要知道某个任务的执行时间段是否跟已知的时间段有重叠，揭开这些特定需求的外表，本质的问题可以这样描述：在一个线性的空间中，已存在很多区间段分布在该线性空间中，现给出一个指定的区间段，求出空间中所有和该区间段有重叠的空间段集合。

定义区间重叠

怎样定义“两个区间重叠”？大家都能立刻判断出这个结果，但是我们要用语言定义出来，或者用数学公式表达出来才能建立解决模型。先看下面一张图：



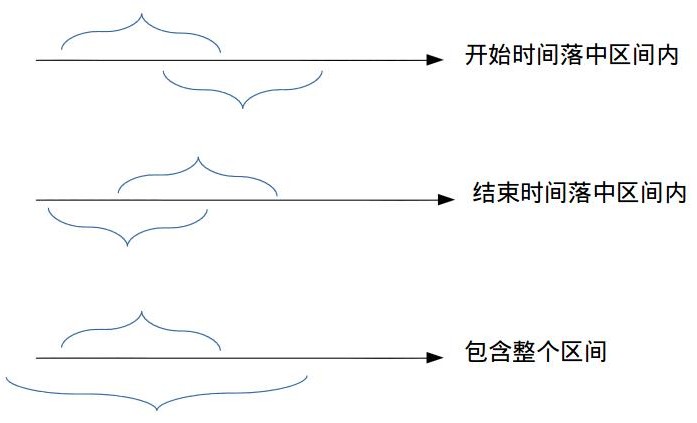
我们把上面的区间叫做t1，下面的区间叫做t2，根据上图可以看出，区间t2和区间t1有重叠的话，必然要满足下列三种情况之一：

1. t2的开始时间落在t1区间段内
2. t2的结束时间落在t1区间段内
3. t2直接包含了整个t1区间

如果我们用数学公式表达的话，就是:

\begin{equation}
t2_{starttime} = t1_{starttime}
\end{equation}

穷举法

根据上面的公式，穷举所有区间集合中的元素，逐个计算，两两比较，返回所有满足要求的区间元素。时间计算复杂度是 \(\theta(N)\)

交集

根据上面的公式1，可以构建两个有序集合，分别存放所有区间段的开始时间和结束时间，假设两个集合分别是 S 和 E，则查询和指定区间(s,e)重叠的所有区间可以这样计算：先计算集合S中所有小于e的元素，再计算出集合E中所有大于s的元素，计算出这两个结果的交集，则为最终结果。用公式表达就是：

\begin{equation}
\{x|x \in S \land x \leq e \} \cap \{y|y \in E \land y \geq s \}
\end{equation}

在具体系统开发中，实现方式有多种。如果基于数据库，如MySQL，可以直接通过`Merge Index`利用两个索引字段。Redis中也有集合的交集运算实现`ZINTERSTORE`。这种方式从直观感觉上比穷举法好像快很多。我们可以大概计算评估下：第一步是要从两个集合中范围查找子集，采用一般的`树结构`，都能做到 $\theta(\log{N})$，第二步要做两个子集的交集运算，复杂度又回到了 $\theta(N)$。这其实和上面的穷举法感觉没有什么区别。

初识IntervalTree算法

其实各种各样的树结构，都是利用二分原理快速找到需要的数据，其复杂度都是 \(\theta(\log{N})\)级。IntervalTree也是利用这一特性，把每个区间二分对折，淘汰掉另外一半来快速找到所要区间数据。

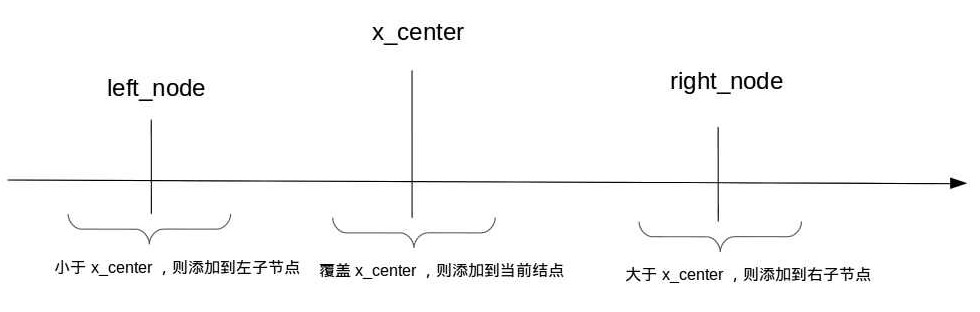
构建

构建一个IntervalTree很简单，每次添加一个区间元素t时，先比较区间t是否覆盖x_center（x_center就是当前整个区间的中间点，从算法效率上来讲，不应该是区间起点和终点的平均值，而应该是落中这个区间内所有元素的中位值）值，如果覆盖则把区间的开始值和结束值分别存放在该节点的两个有序集合中，分别是所有覆盖区间的开始时间集合和结束时间集合。如果区间t在x_center之后，则放到右子节点上，处理方式一样（递归处理）；如果区间t在x_center之前，则放到左子点上，也是递归处理。这样每个节点的数据结构大概这样：

class Node(object):
    def __init__(self, boundary):
        # 区间范围
        self.boundary = boundary
        # 中间值
        self.x_center = (boundary[1] - boundary[0]) / 2 + boundary[0]
        # 左子节点，该节点下的所有区间都小于x_center
        self.left = None
        # 右子节点，该节点下的所有区间都大于x_center
        self.right = None
        # 覆盖x_center的所有节点的开始时间集合
        self.begins = []
        # 覆盖x_center的所有节点的结束时间集合
        self.ends = []
    def add_overlap_interval(self, start_point, end_point):
        self.begins.append(start_point)
        self.begins = sorted(self.begins)
        self.ends.append(end_point)
        self.ends =  sorted(self.ends)

boundary参数表左该节点所能影响到整个区间范围，包含了一个起点和终点。这里简单的把x_center值取成范围的中间值。left 和 right 分别为左子节点和右子节点。begins为有序集合，里面的元素为所有满足特定条件（覆盖x_center）的区间的开始值。同begins一样，ends存放的是所有覆盖x_center的区间的结束值的有序集合。方法add_overlap_interval的作用就是添加能覆盖x_center的间到此节点中。

有了上面描述的节点定义，IntervalTree就是由上述节点组成的，即然是树结构，所以就有根节点的概念。每个IntervalTree有一个根节点。

class IntervalTree(object):
    def __init__(self, min_point, max_point):
        self.min_point = min_point
        self.max_point = max_point
        self.root = Node((min_point, max_point))
    def add(self, start_point, end_point):
        node = self.root
        while end_point < node.x_center or start_point > node.x_center:
        # 如果区间没有覆盖x_center，则添加到子节点中去
            if end_point < node.x_center:
            # 添加到左子节点
                if not node.left:
                    node.left = Node((node.boundary[0], node.x_center))
                node = node.left
            else:
            # 添加到右子节点
                if not node.right:
                    node.right = Node((node.x_center, node.boundary[1]))
                node = node.right
        else:
        # 区间覆盖x_center，则添加到此节点
            node.add_overlap_interval(start_point, end_point)

查询

对于一个区间集合 S，对于给定的区间 q，现要查询出所有和区间 q 有重叠的区间子集合，怎样做呢？根据前面的区间重叠定义中说的，如果一个区间的开始时间或者结束时间落在了另外一个区间内，或者完全包含这个区间，则是重叠的。所以我们按照这个思路分别求解。

先查出所有点（无论开始时间或结束时间点）落在查询区间 q 段内的数据。这点很好做，可以把所有开始时间和结束时间放在一个排序的数据结构中（如红黑树），这样求解就转换成了在一个树中求范围数据，其复杂度是 \(\theta(\log{N})\)。

再找出那些区间完全包含了查询区间q的数据。这里有个技巧可以利用，在区间q中随便取一个点p，我们可以有如下结论推理：凡是区间能覆盖到点p的，则肯定和区间q有重叠。这个用数学公式很好推理出来。所以现在的问题就是在一个IntervalTree树中查出给定一个点的所有覆盖区间子集合。这个问题的求解和构建树结构一致。从根节点开始查询，查询此节点中所有可覆盖的区间。然后根据指定点落在左，或右子节点上来２分查找，直到没有没有子节点时退出。这里要注意一点：如果指定点刚好等于x_center点，则立即停止查找子节点，并返回当前节点所包含的所有区间数据。查找算法如下：

    def search_intervals(self, point):
      　 # 从根节点开始查找
        node = self.root
        result = []
        while point != node.x_center:
        # 如果查找点没有和x_center相同
            if point < node.x_center:
            # 如果查找点在x_center前边，则该节点内所有的区间中，开始时间早于或者等于point的区间都是覆盖point的
                result += [s for s in node.begins if s <= point]
                node = node.left
            else:
            # 如果查找点在x_center后边，则该节点内所有的区间中，结束时间晚于或者等于point的区间都是覆盖point的
                result += [s for s in node.ends if s >= point]
                node = node.right
            if not node:
                break
        else:
            result += node.begins
        return result

至此，整个IntervalTree的大概思路表述完了。上面的代码其实更多的是讲述思路，细节没有注意，比如Node结构中begins和ends用LinkedList还是RBTree更合适。还有其它一些思考，比如区间的删除，以及具体数据业务场景中，选择什么样的x_center的取值方式使树更平衡些。留言下说你的思考，谢谢！

参考：wiki_IntervalTree