C#数据结构_图

顶点的度=顶点的入度+顶点的出度。

顶点 v 的入度是指以该顶点 v 为弧头的弧的数目；顶点 v 的出度是指以该顶点 v 为弧尾的弧的数目。

简单路径：一条路径上顶点不重复出现。

回路：第一个顶点和最后一个顶点相同的路径。

简单回路：除第一个顶点和最后一个顶点相同其余顶点都不重复的回路。

连通：在无向图中，若两个顶点之间有路径。

连通图：无向图 G 中任意两个顶点之间都是连通的。

强连通图：在有向图中，若图中任意两个顶点之间都存在从一 个顶点到另一个顶点的路径。

最小生成树：边的权值总和最小的生成树。

构造有 n 个顶点的无向连通网的最小生成树必须 满足以下三个条件：

（1）构造的最小生成树必须包括 n 个顶点；

（2）构造的最小生成树有且仅有 n-1 条边；

（3）构造的最小生成树中不存在回路。

构造最小生成树的方法：普里姆(Prim)；克鲁斯卡尔(Kruskal)算法。

普里姆(Prim)：

假设 G=（V，E）为一无向连通网，其中，V 为网中顶点的集合，E 为网中 边的集合。设置两个新的集合 U 和 T，其中，U 为 G 的最小生成树的顶点的集 合，T 为 G 的最小生成树的边的集合。普里姆算法的思想是：令集合 U 的初值 为 U={u1}（假设构造最小生成树时从顶点 u1 开始），集合 T 的初值为 T={}。从 所有的顶点 u∈U 和顶点 v∈V-U 的带权边中选出具有最小权值的边（u,v），将顶 点 v 加入集合 U 中，将边（u,v）加入集合 T 中。如此不断地重复直到 U=V 时， 最小生成树构造完毕。此时，集合 U 中存放着最小生成树的所有顶点，集合 T中存放着最小生成树的所有边。

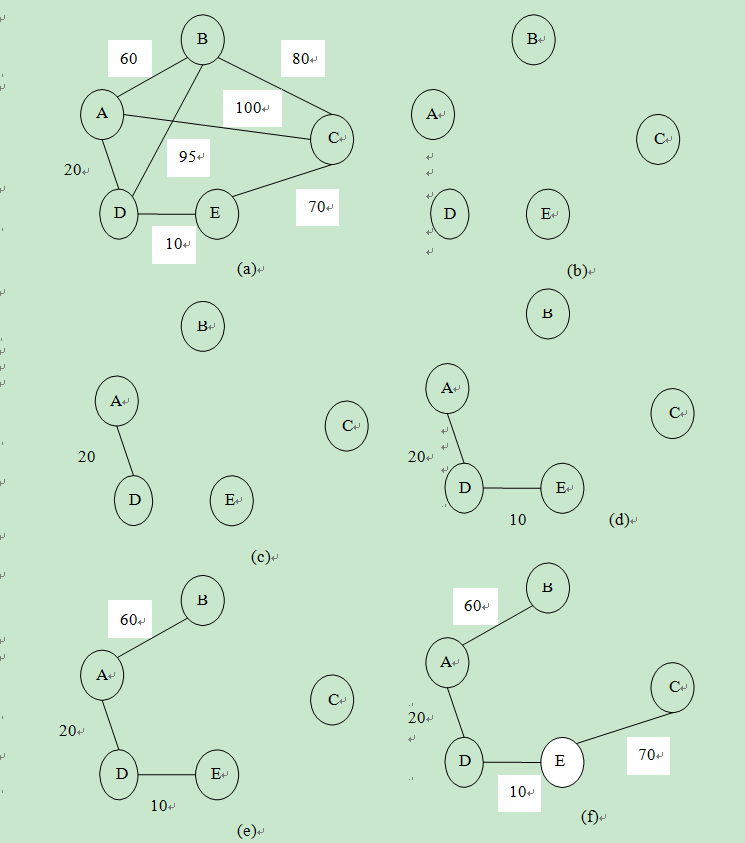
克鲁斯卡尔(Kruskal)算法：对一个有 n 个顶点的无向连通网，将图中的 边按权值大小依次选取，若选取的边使生成树不形成回路，则把它加入到树中； 若形成回路，则将它舍弃。如此进行下去，直到树中包含有 n-1 条边为止。

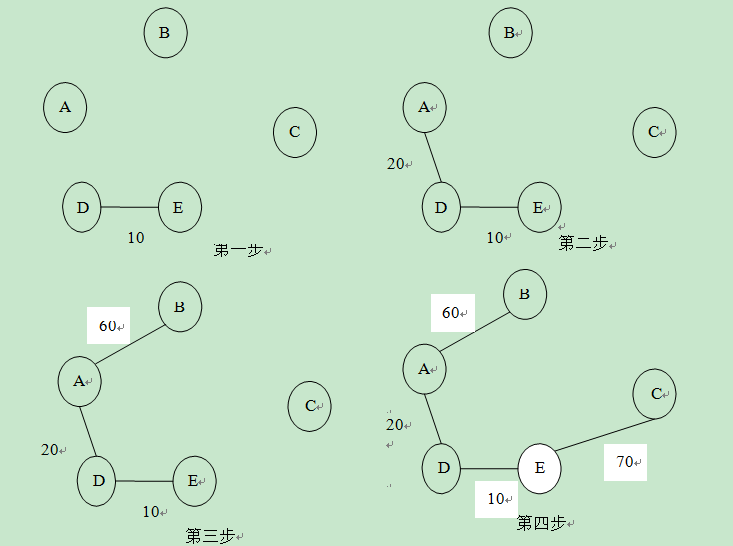
最短路径：狄克斯特拉（Dikastra）算法：设置 两个顶点的集合 S 和 T，集合 S 中存放已找到最短路径的顶点，集合 T 中存放当 前还未找到最短路径的顶点。初始状态时，集合 S 中只包含源点，设为 v0，然 后从集合 T 中选择到源点 v0 路径长度最短的顶点 u 加入到集合 S 中，集合 S 中 每加入一个新的顶点 u 都要修改源点 v0 到集合 T 中剩余顶点的当前最短路径长 度值，集合 T  中各顶点的新的最短路径长度值为原来的当前最短路径长度值与 从源点过顶点 u 到达该顶点的新的最短路径长度中的较小者。此过程不断重复， 直到集合 T 中的顶点全部加到集合 S 中为止。