【bzoj3028】 食物 生成函数+隔板法
题目传送门:https://www.lydsy.com/JudgeOnline/problem.php?id=3028
这题的推导很妙啊,裸的推母函数的题。
我们首先构造出每种食物的母函数:
汉堡:$1+x^2+x^4+……=\frac{1}{1-x^2}$
可乐:$1+x=\frac{1-x^2}{1-x}$
鸡腿:$1+x+x^2=\frac{1-x^3}{1-x}$
蜜桃:$x+x^3+x^5+......=\frac{x}{1-x^2}$
鸡块:$1+x^4+x^8+......=\frac{1}{1-x^4}$
包子:$1+x+x^2+x^3=\frac{1-x^4}{1-x}$
炒肉:$1+x=\frac{1-x^2}{1-x}$
面包:$1+x^3+x^6+......=\frac{1}{1-x^3}$
然后,我们将这八个母函数乘起来,得到$\frac{x}{(1-x)^4}$,所求答案为$\frac{x}{(1-x)^4}$的n次项系数。
考虑如何求这个东西,不难发现,$\frac{x}{(1-x)^4}=x \times (\frac{1}{1-x})^4$,然后又因为$\frac{1}{1-x}=\sum_{i=0}{\infty} x^i$,可以想象成有一个物品集合A,其中每种权值恰好有1个,那么$\frac{x}{(1-x)^4}$的n次项系数相当于从4个A集合中各取出1个,并且这4个物品的权值和为n的方案数,这个东西通过插板法简单推导下可以推出其答案为$\binom{n+2}{3}$。
由于n很大,读入的时候先取个模再求答案即可。
代码很短,推导稍长....
#include<bits/stdc++.h>
#define MOD 10007
#define INV6 1668
using namespace std;
char c[]={}; int main(){
scanf("%s",c);
int len=strlen(c),n=;
for(int i=;i<len;i++) n=(n*+c[i]-'')%MOD;
printf("%d\n",n*(n+)%MOD*(n+)%MOD*INV6%MOD);
}
【bzoj3028】 食物 生成函数+隔板法的更多相关文章
- BZOJ 3028: 食物 [生成函数 隔板法 | 广义二项式定理]
3028: 食物 Time Limit: 3 Sec Memory Limit: 128 MBSubmit: 497 Solved: 331[Submit][Status][Discuss] De ...
- BZOJ3028食物——生成函数+泰勒展开
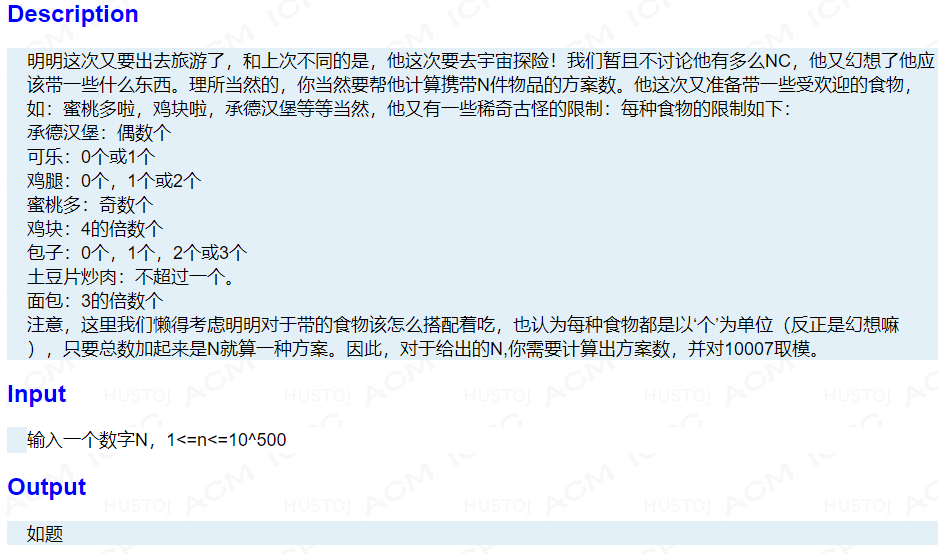
题目描述 明明这次又要出去旅游了,和上次不同的是,他这次要去宇宙探险!我们暂且不讨论他有多么NC,他又幻想了他应 该带一些什么东西.理所当然的,你当然要帮他计算携带N件物品的方案数.他这次又准备带一些 ...
- BZOJ3028: 食物(生成函数)
题意 链接 Sol 生成函数入门题. 对每个物品分别列一下,化到最后是\(\frac{x}{(1-x)^4}\) 根据广义二项式定理,最后答案是\(C_{(N - 1) + 4 - 1}^{4-1} ...
- BZOJ3028 食物 和 LOJ6261 一个人的高三楼
总结一下广义二项式定理. 食物 明明这次又要出去旅游了,和上次不同的是,他这次要去宇宙探险!我们暂且不讨论他有多么NC,他又幻想了他应该带一些什么东西.理所当然的,你当然要帮他计算携带N件物品的方案数 ...
- CF451E Devu and Flowers (隔板法 容斥原理 Lucas定理 求逆元)
Codeforces Round #258 (Div. 2) Devu and Flowers E. Devu and Flowers time limit per test 4 seconds me ...
- vijos1060 隔板法
排列组合问题 之前没有学过隔板法,随便学习了一下 其实挺好理解的 附上题解: 先只考虑一种球:因为有n个盒子每个盒子可以放任意多球,还可以空出来任意多球.所以可以考虑为n+1个盒子,最后一个盒子里面是 ...
- How do you add? UVA - 10943(组合数的隔板法!!)
题意: 把K个不超过N的非负整数加起来,使它们的和为N,有多少种方法? 隔板法...不会的可以买一本高中数学知识清单...给高中班主任打个广告.... 隔板法分两种...一种是不存在空集 = C(n- ...
- 51Nod 1509 加长棒(隔板法)
http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1509 思路: 直接去解可行的方法有点麻烦,所以应该用总的方法去减去不可行 ...
- uva10943(隔板法)
很裸的隔板法. 引用一下维基上对隔板法的解释: 现在有10个球,要放进3个盒子里 ●●●●●●●●●● 隔2个板子,把10个球被隔开成3个部份 ●|●|●●●●●●●●.●|●●|●●●●●●●.●| ...
随机推荐
- 【Mac】使用QuickTime Player录制屏幕录像
我门分享都需要用到录屏软件,Mac系统有自带的QuickTime Player软件可以录制屏幕录像 环境与工具 1.mac系统 2.mac自带的QuickTime Player软件 使用方法 1.打开 ...
- phalApi数据库操作
在很多时候,我们会遇到数据库表里面的某个值需要+1操作,我们不能简单地在update的时候写入array('key' => 'key+1'),因为在解析sql的时候,key+1 会带上引号作为一 ...
- 在centos7.1上安装systemd
1.检查本地systemd的版本 [admin@localhost ~]$ systemctl --version systemd 208 +PAM +LIBWRAP +AUDI ...
- java redis基本操作
package com.redis; import java.util.ArrayList;import java.util.Iterator;import java.util.List;import ...
- Field '***********' doesn't have a default value
今天做配置文件一直报这个错误: 原因是主键是integer类型,没有设置自增模式,所以会出现这个问题,是表的结构问题.更改用navicat
- HDU 2106 decimal system (进制转化求和)
题意:给你n个r进制数,让你求和. 析:思路就是先转化成十进制,再加和. 代码如下: #include <iostream> #include <cstdio> #includ ...
- AE(ArcEngine)定制工具Tool工具箱
using System; using System.Collections.Generic; using System.Text; using System.Runtime.InteropServi ...
- JAVA“动态”为类添加属性
部分参考:http://www.cnblogs.com/zy2009/p/6725843.html pom.xml中添加: <dependency> <groupId>comm ...
- Informatica增量抽取时间的设置
使用数据库或者系统变量的当前时间 Informatica中的$$SYSDATE是表示当前系统时间的系统变量. 通过这个变量,我们对每天抽取的数据可以使用以下表达式来实现增量抽取: 时间戳字段>= ...
- 别具光芒Div CSS 读书笔记(一)
继承 边框(border).边界(margin).填充(padding).背景(background) 是不能继承的. table 中td不会继承body的属性,因此需要单独指定. 权重 ...
