深入浅出“跨视图粒度计算”--3、EXCLUDE表达式

本文由  网易云发布。

深入嵌入“跨视图粒度计算”的前面两篇分别讲了

1、理解数据的粒度

2、INCLUDE表达式

这一篇讲一下EXCLUDE表达式的用法。

EXCLUDE，中文译为“排除”，顾名思义，这个表达式和INCLUDE表达式是对立的，语法规则如下：

{ EXCLUDE [维度] : 聚合表达式 }

比如我们先做了下图，看了每个“类别”下，各个子类别的总销售额

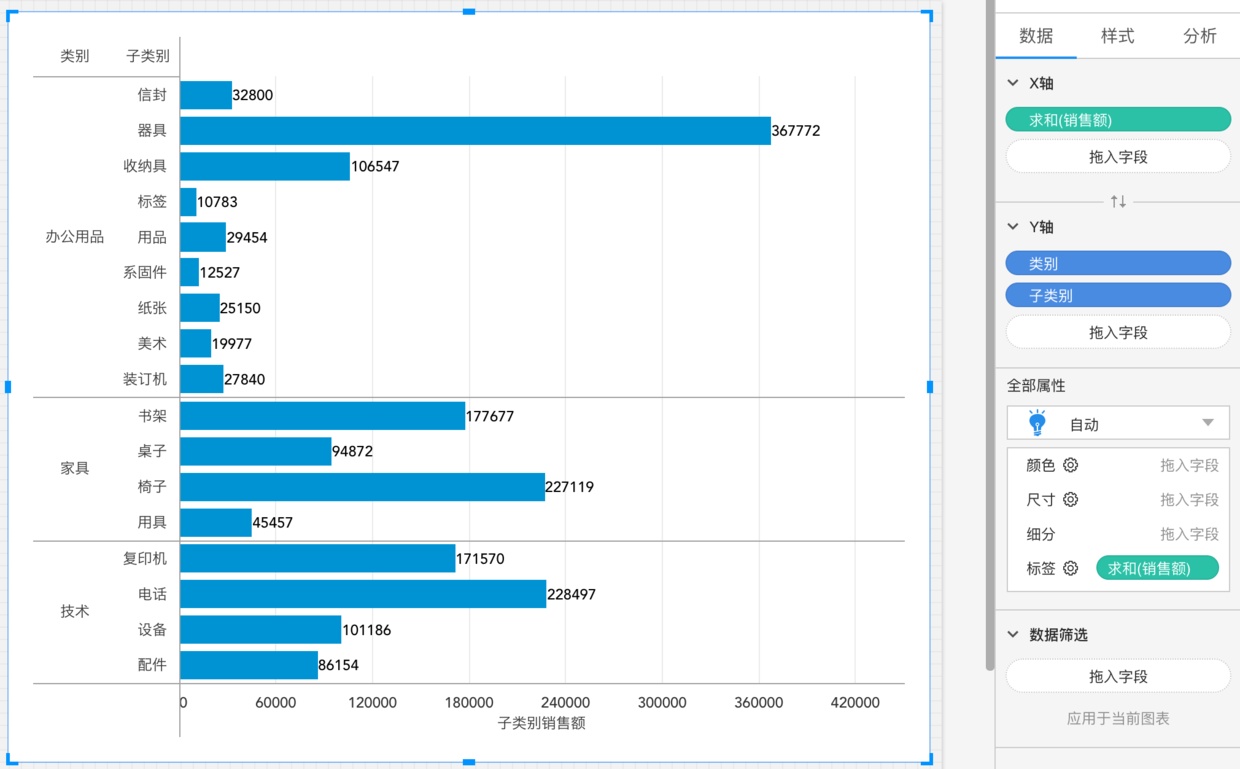
如果此时我们想在这张图上看每个类别的总销售额，那该怎么做呢？

我们可以使用EXCLUED表达式细来完成此要求。我们排除“子类别”维度。我们新建一个计算字段，名为 “销售额 Exclude 子类别”：

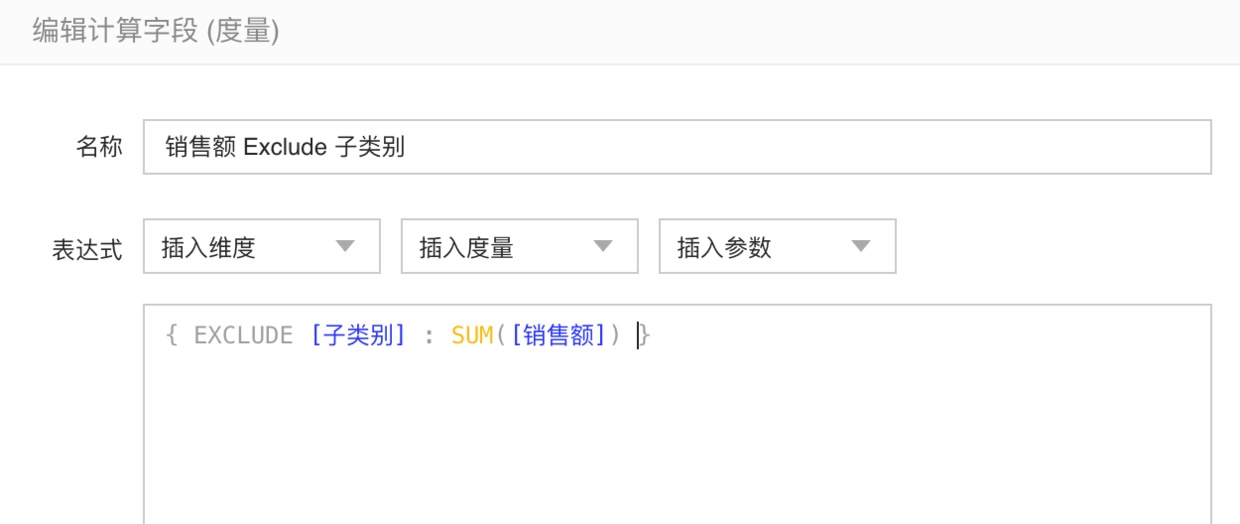
Exclude 子类别

此时，我们再把“销售额 Exclude 子类别”字段拖入图表，可以得到下图

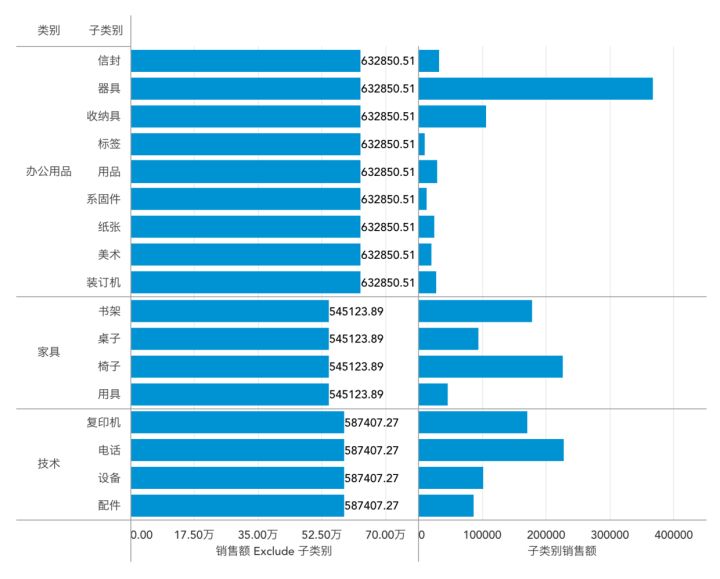
EXCLUDE

此时我们在同一张图表上，既可以看到每个“子类别”的总销售额，也可以看到每个“类别”的总销售额。所以在这个例子里面，图表的面板上有

{ EXCLUDE [子类别] : SUM([销售额]) }

这个表达式，排除了“子类别”这个维度，相当于我们做了下图，

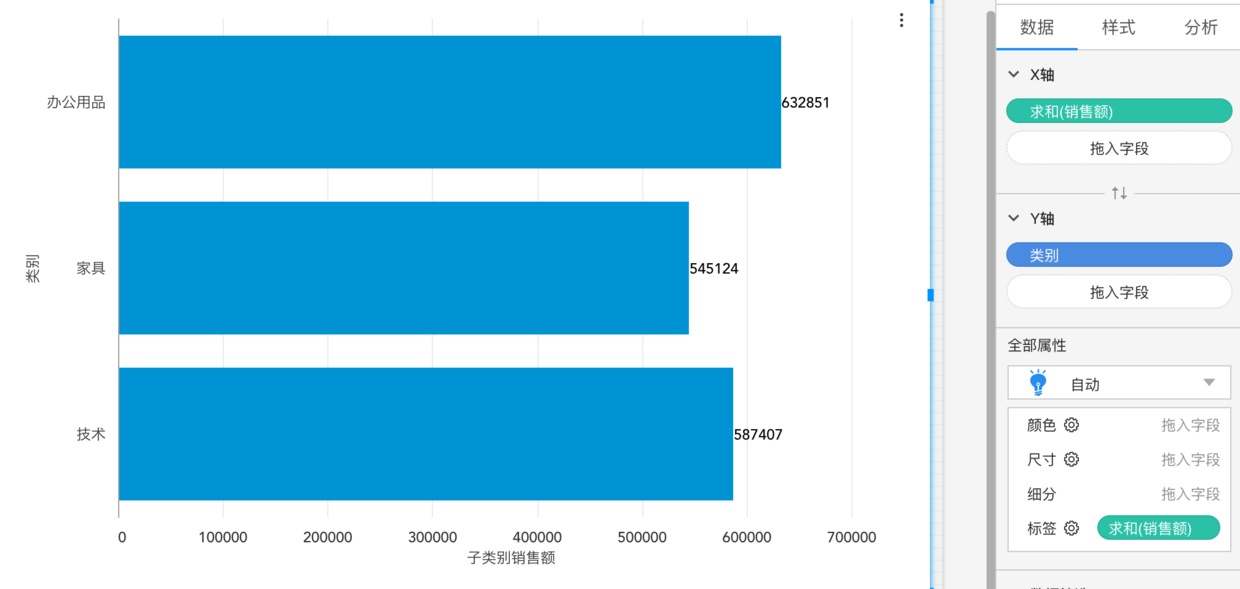
每个类别的销售额

然后在聚合回了图表的真实粒度。

网易有数，企业级大数据可视化分析平台，具有全面的安全保障、强大的大数据计算性能、先进的智能分析、便捷的协作分享等特性。可以点击这里免费试用。

了解 网易云 ：
网易云官网：https://www.163yun.com/
新用户大礼包：https://www.163yun.com/gift
网易云社区：https://sq.163yun.com/