高效求a的n次幂的算法
代码:
public class A的N次幂 {
public static void main(String[] args) {
int a = 2;
int n = 60;
long t = System.nanoTime(); // 纳秒
System.out.println(pow0(a, n));
System.out.println("pow0()所花时间:"+(System.nanoTime()-t)+"ns");
t = System.nanoTime();
System.out.println(pow(a, n));
System.out.println("pow()所花时间:"+(System.nanoTime()-t)+"ns");
}
// O(N)
private static long pow0(int a,int n){
long res = 1;
for(int i=0;i<n;i++){
res *= a;
}
return res;
}
private static long pow(int a,int n){
if (n==0) {
return 1;
}
long res = a;
int ex = 1;
while((ex<<1)<=n){
res = res * res;
ex <<=1;
}
return res*pow(a, n-ex);
}
}
结果:
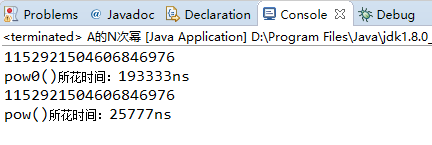
高效求a的n次幂的算法的更多相关文章
- 华为上机:求2的N次幂的值
求2的N次幂的值 描述: 求2的N次幂的值(N最大不超过31,用位运算计算,结果以十六进制进行显示). 运行时间限制: 无限制 内存限制: 无限制 输入: 数字N 输出: 2的N次方(16进制,需要按 ...
- 求用delphi编写的LRC校验位算法函数,急!!!
求用delphi编写的LRC校验位算法函数,急!!! 某命令串为":010200000001FC" 其16进制为“3A 30 31 30 32 30 30 30 30 30 30 ...
- c语言求回文数的三种算法的描述
c语言求回文数的三种算法的描述 题目描述 注意:(这些回文数都没有前导0) 1位的回文数有0,1,2,3,4,5,6,7,8,9 共10个: 2位的回文数有11,22,33,44,55,66,77,8 ...
- 高效求幂取余 算法,复杂度 log(n)
做TopCoder SRM 576 D2 L3 题目时,程序有个地方需要对一个数大量求幂并取余,导致程序运行时间很长,看了Editoral之后,发现一个超级高效的求幂并取余的算法,之前做System ...
- UOJ424 Count 生成函数、多项式求逆、矩阵快速幂
传送门 两个序列相同当且仅当它们的笛卡尔树相同,于是变成笛卡尔树计数. 然后注意到每一个点的权值一定会比其左儿子的权值大,所以笛卡尔树上还不能够存在一条从根到某个节点的路径满足向左走的次数\(> ...
- AtCoder AGC019E Shuffle and Swap (DP、FFT、多项式求逆、多项式快速幂)
题目链接 https://atcoder.jp/contests/agc019/tasks/agc019_e 题解 tourist的神仙E题啊做不来做不来--这题我好像想歪了啊= =-- 首先我们可以 ...
- hdu 1575 求一个矩阵的k次幂 再求迹 (矩阵快速幂模板题)
Problem DescriptionA为一个方阵,则Tr A表示A的迹(就是主对角线上各项的和),现要求Tr(A^k)%9973. Input数据的第一行是一个T,表示有T组数据.每组数据的第一行有 ...
- python——用递归的方法求x的y次幂
def function(x,y): : : )*x ): number = int(input('请输入x的值:')) y = int(input('请输入y的值:')) print('x的y次幂的 ...
- NYOJ——301递推求值(矩阵快速幂)
递推求值 时间限制:1000 ms | 内存限制:65535 KB 难度:4 描述 给你一个递推公式: f(x)=a*f(x-2)+b*f(x-1)+c 并给你f(1),f(2)的值,请求出f(n)的 ...
随机推荐
- 概率dp的边界处理 POJ 2096
题目地址:https://vjudge.net/problem/POJ-2096 说的是有n个bug,和s个系统.现在一个人一天能发现一个bug,它可能是任何一个系统中的,也可能会发现已经发现过的bu ...
- 如何设置PDF签名文档,PDF签名文档怎么编辑
在工作中我们都会遇到有文件需要签名的时候,如果是在身边就直接拿笔来签名了,那么如果没有在身边又是电子文件需要签名的时候应该怎么办呢,这个时候就应该设置一个电子的签名文档,其他的文件电子文件签名很简单, ...
- bootstrap学习(二)页面
响应式图片: //当图片大的时候,逐渐缩小浏览器大小,图片会显示为自适应大小 ,img-responsive <div class="container"> <d ...
- java 静态代理模式
package proxy.staticproxy; public interface IStar { public void sing(); } package proxy.staticproxy; ...
- Linux scp 命令卡住的原因
When transferring large files(for example mksysb images) using scp through a firewall, the scp conne ...
- C. 新年的繁荣
题解: 用最小生成树的Boruvka算法 即每次找到每个点不在它联通块的边内的最大值 然后进行log次这个过程 然后找这个的话我们可以用trie树在2^m的时间内完成建树(如果是1要合并到0上)
- 通过iis访问电脑文件
新公司没有开发环境,移动端项目,需要自己在手机上先进行查看效果,提供了一个方法iis,之前有听过,但是一直没有用过,今天来记录一下这个配置过程: 环境:win10 1.安装iis 控制面板——程序—— ...
- 树莓派B+使用入门&RPI库安装&wringPi库安装
最近看看试用一下树莓派进行一些开发操作,于是入手一块Raspberry Pi B+的板子来玩.由于没有显示器,没有备用的键盘和鼠标,所以想到用SSH来控制树莓派,刚开始还很担心已经安装好的操作系统到底 ...
- 按键精灵PC版<末日王者>
更新模式[强制] 更新版本[1.28] 更新链接[https://yunfei-1256035889.cos.ap-beijing.myqcloud.com/%E6%9C%AB%E6%97%A5%E4 ...
- 二、自动化测试平台搭建-搭建jango环境
上篇说的是安装虚拟环境,后面的项目全部放在虚拟环境上 1.创建一个虚拟环境py3,进入虚拟环境 2.安装django包:pip install django==1.8.2 3.在家目录下的Deskto ...
