dp算法之平安果路径问题c++

前文：https://www.cnblogs.com/ljy1227476113/p/9563101.html

在此基础上更新了可以看到行走路径的代码。

代码：

 #include <iostream>
 using namespace std;
 int ivec[][];
 int dp[][];
 int que[];
 int main()
 {
     int m, n;
     int i, j;
     int tail = ;
     while (cin >> m >> n)
     {
         que[] = {  };
         for (i = ; i <= m; i++)
         {
             for (j = ; j <= n; j++)
             {
                 cin >> ivec[i][j];
             }
         }
         que[] = ivec[m][n];
         dp[][] = ivec[][];
         for (i = ; i <= m; i++)
         {
             dp[i][] = dp[i - ][]+ivec[i][];
         }
         for (j = ; j <= n; j++)
         {
             dp[][j] = dp[][j - ]+ivec[][j];
         }
         for (i = ; i <= m; i++)
         {
             for (j = ; j <= n; j++)
             {
                 dp[i][j] = ((dp[i - ][j] < dp[i][j - ]) ? dp[i][j - ] : dp[i - ][j]) + ivec[i][j];
             }
         }
         i = m, j = n;
         while(tail <= m + n - )
         {
             if (dp[i - ][j] >= dp[i][j - ])
             {
                 que[tail++] = ivec[i - ][j];
                 i--;
             }
             else
             {
                 que[tail++] = ivec[i][j - ];
                 j--;
             }
         }
         for (i = ; i <= m; i++)
         {
             for (j = ; j <= n; j++)
                 cout << dp[i][j] << " ";
             cout << endl;
         }
         for (i = m + n - ; i >= ; i--)
             cout << que[i] << " ";
         cout << endl;
         cout << dp[m][n] << endl;
     }
     return ;
 }

结果：

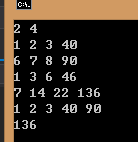
输入：

2 4

1 2 3 40

6 7 8 90

输出：

1 2 3 40 90

136