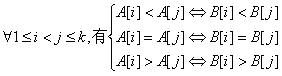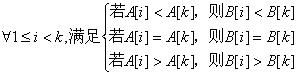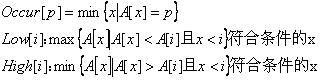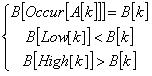POJ 3167 Cow Pattern ★(KMP好题)
题意
给你一个数字序列S,再给一个数字序列pattern,S和pattern中的数字都是1到s(s<=25)。每个序列里的数字都有个排名,也就是第几小,现在我们要用pattern来匹配S。在本题中匹配是指每个数字的排名都一样,即同是第k小,最后输出匹配的所有位置。
思路
KMP好题,对KMP的理解又透彻了一点点~
我们考虑两个字符串A,B
在此题中,A[1],A[2],…,A[k]与B[1],B[2],…,B[k]匹配条件:
若A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,则加上A[k]与B[k]仍然匹配的条件是:
必须在与k无关的时间复杂度内完成该操作
然而,由于A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]已经匹配,可以简化比较操作
考虑到字符集很小(不超过25),我们可以定义以下几个变量:
Occur[p],Low[i],High[i]可能不存在,若存在则取最小的符合条件的x
则A[1],A[2],…,A[k-1]与B[1],B[2],…,B[k-1]匹配,加上A[k]与B[k]仍然匹配的条件可简化为:
接下来就可以用O(SK)时间内预处理求出Occur[p],Low[i],High[i],然后套用kmp算法,总时间复杂度为O(N+SK)
代码
[cpp]
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <string>
#include <cstring>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#define MID(x,y) ((x+y)/2)
#define MEM(a,b) memset(a,b,sizeof(a))
#define REP(i, begin, end) for (int i = begin; i <= end; i ++)
using namespace std;
typedef long long LL;
int n, k, s;
int S[100005], pattern[25005];
int low[25005], high[25005], ranks_pos[30], next[100005];
vector <int> ans;
void init(){
MEM(ranks_pos, -1); MEM(low, -1); MEM(high, -1);
for (int i = 0; i < k; ++ i){
int j = pattern[i] - 1;
while(j){
if (~ranks_pos[j]){ low[i] = j; break; }
j --;
}
j = pattern[i] + 1;
while(j < s+1){
if (~ranks_pos[j]){ high[i] = j; break; }
j ++;
}
if (ranks_pos[pattern[i]] == -1)
ranks_pos[pattern[i]] = i;
}
}
bool check(int A[], int B[], int k, int pos){
if (~ranks_pos[A[pos]]){
if (B[k+ranks_pos[A[pos]]] != B[k+pos]) return false;
}
if (~low[pos] && ~ranks_pos[low[pos]]){
if (B[k+ranks_pos[low[pos]]] >= B[k+pos]) return false;
}
if (~high[pos] && ~ranks_pos[high[pos]]){
if (B[k+ranks_pos[high[pos]]] <= B[k+pos]) return false;
}
return true;
}
void get_next(){
int j = -1;
next[0] = -1;
for (int i = 1; i < k; ++ i){
while(j > -1 && !check(pattern, pattern, i-j-1, j+1)) j = next[j];
if (check(pattern, pattern, i-j-1, j+1)) j ++;
next[i] = j;
//printf("next%d = %d\n", i, next[i]);
}
}
void kmp(){
ans.clear();
get_next();
int j = -1;
for (int i = 0; i < n; ++ i){
while(j > -1 && !check(pattern, S, i-j-1, j+1)) j = next[j];
if (check(pattern, S, i-j-1, j+1)) j ++;
if (j == k - 1){
ans.push_back(i - k + 1);
j = next[j];
}
}
}
int main(){
while(scanf("%d %d %d", &n, &k, &s) != EOF){
for (int i = 0; i < n; i ++) scanf("%d", &S[i]);
for (int i = 0; i < k; i ++) scanf("%d", &pattern[i]);
init();
kmp();
printf("%d\n", ans.size());
for (int i = 0; i < (int)ans.size(); ++ i){
printf("%d\n", ans[i]+1);
}
}
return 0;
}
[/cpp]
POJ 3167 Cow Pattern ★(KMP好题)的更多相关文章
- POJ 3167 Cow Patterns (KMP+前缀和)
题意:给你两串数字,长度分别为n和m,数字大小在[1,25].当后一串数字每个数字的排名位置与前一串数字(任一长度为m的子串)每个数字的排名位置一致时就完全匹配,最后求哪些位置是完全匹配的. 例如:1 ...
- POJ 3167 Cow Patterns(模式串浮动匹配)
题目链接:http://poj.org/problem?id=3167 题意:模式串可以浮动的模式匹配问题给出模式串的相对大小,需要找出模式串匹配次数和位置. 思路:统计比当前数小,和于当前数相等的, ...
- POJ:3461-Oulipo(KMP模板题)
原题传送:http://poj.org/problem?id=3461 Oulipo Time Limit: 1000MS Memory Limit: 65536K Description The F ...
- POJ 3176 Cow Bowling (水题DP)
题意:给定一个金字塔,第 i 行有 i 个数,从最上面走下来,只能相邻的层数,问你最大的和. 析:真是水题,学过DP的都会,就不说了. 代码如下: #include <cstdio> #i ...
- poj 3461 Oulipo(KMP模板题)
Oulipo Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 36903 Accepted: 14898 Descript ...
- POJ 3461 Oulipo(KMP裸题)
Description The French author Georges Perec (1936–1982) once wrote a book, La disparition, without t ...
- POJ Oulipo KMP 模板题
http://poj.org/problem?id=3461 Oulipo Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 4 ...
- POJ Oulipo(KMP模板题)
题意:找出模板在文本串中出现的次数 思路:KMP模板题 #include<cstdio> #include<cstring> #include<cmath> #in ...
- POJ 3045 Cow Acrobats (贪心)
POJ 3045 Cow Acrobats 这是个贪心的题目,和网上的很多题解略有不同,我的贪心是从最下层开始,每次找到能使该层的牛的风险最小的方案, 记录风险值,上移一层,继续贪心. 最后从遍历每一 ...
随机推荐
- Ajax跨域请求 同源策略与Jsonp
同源策略 同源策略(Same origin policy)是一种约定,它是浏览器最核心也最基本的安全功能,如果缺少了同源策略,则浏览器的正常功能可能都会受到影响.可以说Web是构建在同源策略基础之上的 ...
- SQL Server语句创建数据库和表——并设置主外键关系
简单的创建数据库的 SQL 语句: use master go if exists(select * from sysdatabases where name='Test') begin select ...
- EasyUI合并行
扩展一下 EasyUI 下面湿扩展EasyUI 合并行的方法 $.extend($.fn.datagrid.methods, { autoMergeCells: function (jq, fie ...
- XDU 1022 (数论筛法+前缀和)
解法一:数论筛法+前缀和 //其实题目中f[n]的值可理解为存在多少个整数对使a*b<=n #include<cstdio> #define N 1007 #define maxn ...
- Git-创建和合并分支
本人拜读了廖雪峰老师关于Git的讲述后整理所得 分支就是科幻电影里面的平行宇宙,当你正在电脑前努力学习Git的时候,另一个你正在另一个平行宇宙里努力学习SVN. 如果两个平行宇宙互不干扰,那对现在的你 ...
- leveldb0
leveldb的源代码进行学习,则纯粹是出于一个码农对美好世界进行探究的好奇.接下来将尽可能从源代码上给出leveldb代码的详尽注释,这里先列出自己在阅读前后的主要参考. 0 官方文档http:// ...
- FS-LDM 十大主题
英文名称 中文名称 概念定义 Party 当事人 指银行所服务的任意对象和感兴趣进行分析的各种对象.如个人或公司客户.潜在客户.代理机构.雇员.分行.部门等. Internal Org 内部组织 可能 ...
- MLlib1.6指南笔记
MLlib1.6指南笔记 http://spark.apache.org/docs/latest/mllib-guide.html spark.mllib RDD之上的原始API spark.ml M ...
- CSS Tooltip(提示工具)
CSS Tooltip(提示工具) 提示工具在鼠标移动到指定元素后触发,可以在四个方位显示:头部显示.右边显示.左边显示.底部显示 一.基础提示框(Tooltip) 提示框在鼠标移动到指定元素上显示: ...
- awk二十问-【AWK学习之旅】
---===AWK学习之旅===--- 一行命令: 1.打印输入每行的字段总数: 最后一行的字段总数:END{print NF} 每行都显示字段总数: {print NF} 2.打印指定行: aw ...