POJ 1410--Intersection(判断线段和矩形相交)

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 16322		Accepted: 4213

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
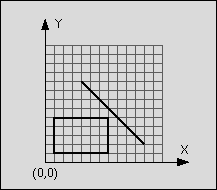
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

Source

Southwestern European Regional Contest 1995

• 题目的判断是否一条线段和矩形相交，可以想到直接判断给定线段是否和矩形的四条边相交即可，但是有一个问题，题目定义的矩形"The rectangle consists of four straight lines and the area in between"，包括了其中的面积，就因为这个wa了几发Orz,我的等级还是不够啊。
• 最后只要判断给定线段是否和矩形的四条边相交，以及线段是否在矩形内，线段是否在矩形内部可以用线段的端点是否在矩形内部来判断。

•  #include<iostream>
   #include<algorithm>
   #include<cmath>
   using namespace std;
   int n;
   double xs, ys, xe, ye, xl, yl, xr, yr;
   const double eps = 1.0e8;
   typedef struct point {
       double x;
       double y;
       point(double a, double b) {
           x = a;
           y = b;
       }
       point() {
  
       }
   }point;
   typedef struct edge {
       point start;
       point end;
       edge(point a, point b) {
           start = a;
           end = b;
       }
       edge() {
  
       }
       edge(edge &t) {
           start = t.start;
           end = t.end;
       }
   }edge;
   point t[];
   edge line;
   edge rec[];
  
   inline double dabs(double a) { return a <  ? -a : a; }
   inline double max(double a, double b) { return a > b ? a : b; }
   inline double min(double a, double b) { return a < b ? a : b; }
   double multi(point p1, point p2, point p0) {
       return (p2.y - p0.y)*(p1.x - p0.x) - (p2.x - p0.x)*(p1.y - p0.y);
   }
   bool Across(edge v1, edge v2) {
       if (max(v1.start.x, v1.end.x) >= min(v2.start.x, v2.end.x) &&
           max(v1.start.y, v1.end.y) >= min(v2.start.y, v2.end.y) &&
           max(v2.start.x, v2.end.x) >= min(v1.start.x, v1.end.x) &&
           max(v2.start.y, v2.end.y) >= min(v1.start.y, v1.end.y) &&
           multi(v2.start, v1.end, v1.start)*multi(v1.end, v2.end, v2.start) >=  &&
           multi(v1.start, v2.end, v2.start)*multi(v2.end, v1.end, v1.start) >=
           )
           return true;
       return false;
   }
   int main(void) {
       while (cin >> n) {
           while (n-- > ) {
               int flag = ;
               cin >> xs >> ys >> xe >> ye >> xl >> yl >> xr >> yr;
               line = edge(point(xs, ys), point(xe, ye));
               t[] = point(xl, yl), t[] = point(xr, yl);
               t[] = point(xr, yr), t[] = point(xl, yr);
               for (int i = ; i < ; i++) {
                   rec[i] = edge(t[i], t[(i + )%]);
               }
               for (int i = ; i < ; i++) {
                   if (Across(line, rec[i]))
                   {
                       flag = ;
                       break;
                   }
               }
               if(line.start.x>=min(xl,xr)&&line.start.x<=max(xr,xl)&&line.start.y>=min(yl,yr)&&line.start.y<=max(yl,yr) ||
                   line.end.x >= min(xl, xr) && line.end.x <= max(xr, xl) && line.end.y >= min(yl, yr) && line.end.y <= max(yl, yr))
                       flag = ;//判断是否点在矩形内部
               if (flag == )
                   cout << "T" << endl;
               else
                   cout << "F" << endl;
           }
       }
       return ;
   }