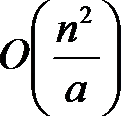bzoj2120 / P1903 [国家集训队]数颜色 / 维护队列(带修改莫队)
带修改的莫队
在原有指针$(l,r)$上又添加了时间指针$t$
贴一段dalao的解释
带修改的莫队,和原版莫队相比,多了一个时间轴
原版莫队是将区间(l,r)视为点(l,r),带修改的即加一维时间轴(l,r,t)
对于t轴的移动可以保存每次修改,如果修改在(l,r)间则更新
分块方法可以参照原版莫队,先将l分块,再讲r分块,同一块的按t排序
块大小为
可以达到最快的理论复杂度
,证明如下
设分块大小为a,莫队算法时间复杂度主要为t轴移动,同r块l,r移动,l块间的r移动三部分
t轴移动的复杂度为
,同r块l,r移动复杂度为
,l块间的r移动复杂度为
三个函数max的最小值当a为
取得,为
给出一个并不严格的假证明
每次查询时:
$t$轴每次最多移动$t$次。而$l,r$指针在块上的组合共$n^{2}/a^{2}$种,故复杂度$O(n^{2}t/a^{2})$
$l$轴每次最多移动$2a$次,最多$n$次。复杂度$O(na)$
$r$轴每次最多移动的次数是一个递减的等差数列:$n,n-a,n-2a.....$,最多共移动$((n+a)(n/a)/2)$次。所以复杂度就是$O(n^{2}/a)$辣
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
void read(int &x){
static char c=getchar();x=;
while(c<''||c>'') c=getchar();
while(''<=c&&c<='') x=x*+(c^),c=getchar();
}
#define N 50005
struct data{int x,y,t,id;}a[N];
struct modi{int id,pre,now;}d[N];
int Len,n,m,Q,T,L,R,tot,b[N],c[],ans[N]; inline int bel(int x){return (x-)/Len+;}
bool cmp(data A,data B){
if(bel(A.x)!=bel(B.x)) return bel(A.x)<bel(B.x);
if(bel(A.y)!=bel(B.y)) return bel(A.y)<bel(B.y);
return A.t<B.t;
}
int main(){
char opt[]; int q1,q2;
read(n);read(m); register int i;
for(i=;i<=n;++i) read(b[i]);
for(i=;i<=m;++i){
scanf("%s",opt),read(q1),read(q2);
if(opt[]=='Q') a[++Q]=(data){q1,q2,T,Q};
else d[++T].pre=b[q1],d[T].id=q1,d[T].now=b[q1]=q2;
}
Len=ceil(exp((log(n)+log(T))/));//bzoj酱紫写会RE,直接sqrt(n)就好辣 虽然复杂度没办法保证....
for(i=T;i;--i) b[d[i].id]=d[i].pre;
sort(a+,a+Q+,cmp);
L=R=; T=; c[b[]]=tot=;
for(int i=,Id;i<=Q;++i){
while(L<a[i].x) tot-=(c[b[L]]==),--c[b[L]],++L;
while(L>a[i].x) --L,tot+=(c[b[L]]==),++c[b[L]];
while(R<a[i].y) ++R,tot+=(c[b[R]]==),++c[b[R]];
while(R>a[i].y) tot-=(c[b[R]]==),--c[b[R]],--R;
while(T<a[i].t){
++T; Id=d[T].id;
if(L<=Id&&Id<=R) tot-=(c[b[Id]]==),--c[b[Id]];
b[Id]=d[T].now;
if(L<=Id&&Id<=R) tot+=(c[b[Id]]==),++c[b[Id]];
}
while(T>a[i].t){
Id=d[T].id;
if(L<=Id&&Id<=R) tot-=(c[b[Id]]==),--c[b[Id]];
b[Id]=d[T].pre; --T;
if(L<=Id&&Id<=R) tot+=(c[b[Id]]==),++c[b[Id]];
}
ans[a[i].id]=tot;
}
for(i=;i<=Q;++i) printf("%d\n",ans[i]);
return ;
}
bzoj2120 / P1903 [国家集训队]数颜色 / 维护队列(带修改莫队)的更多相关文章
- P1903 [国家集训队]数颜色 / 维护队列 带修改莫队
题目描述 墨墨购买了一套N支彩色画笔(其中有些颜色可能相同),摆成一排,你需要回答墨墨的提问.墨墨会向你发布如下指令: 1. Q L R代表询问你从第L支画笔到第R支画笔中共有几种不同颜色的画笔. 2 ...
- 洛谷 P1903 [国家集训队]数颜色 / 维护队列 带修莫队
题目描述 墨墨购买了一套\(N\)支彩色画笔(其中有些颜色可能相同),摆成一排,你需要回答墨墨的提问.墨墨会向你发布如下指令: \(1\). \(Q\) \(L\) \(R\)代表询问你从第\(L\) ...
- Luogu P1903 [国家集训队]数颜色 / 维护队列 (带修莫队)
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> ...
- luogu 1903 [国家集训队]数颜色 / 维护队列 带修改莫队
十分玄学的数据结构~ code: #include <bits/stdc++.h> #define N 1000006 #define setIO(s) freopen(s".i ...
- P1903 [国家集训队]数颜色 / 维护队列 带修改的莫队
\(\color{#0066ff}{ 题目描述 }\) 墨墨购买了一套N支彩色画笔(其中有些颜色可能相同),摆成一排,你需要回答墨墨的提问.墨墨会向你发布如下指令: 1. Q L R代表询问你从第L支 ...
- 题解 洛谷P1903/BZOJ2120【[国家集训队]数颜色 / 维护队列】
对于不会树套树.主席树的本蒟蒻,还是老老实实的用莫队做吧.... 其实这题跟普通莫队差不了多远,无非就是有了一个时间,当我们按正常流程排完序后,按照基本的莫队来,做莫队时每次循环对于这一次操作,我们在 ...
- P1903 [国家集训队]数颜色 / 维护队列(莫队区间询问+单点修改)
题目链接:https://www.luogu.org/problemnew/show/P1903 题目大意:中文题目 具体思路:莫队单点修改+区间询问模板题,在原来的区间询问的基础上,我们要记录当前这 ...
- P1903 [国家集训队]数颜色 / 维护队列
思路 带修莫队的板子 带修莫队只需要多维护一个时间的指针即可,记录一下每个询问在第几次修改之后,再回退或者前进几个修改操作 排序的时候如果a.l和b.l在一个块里,就看r,如果a.r和b.r在一个块里 ...
- P1903 [国家集训队]数颜色 / 维护队列(带修莫队)
题目描述: 墨墨购买了一套N支彩色画笔(其中有些颜色可能相同),摆成一排,你需要回答墨墨的提问.墨墨会向你发布如下指令: 1. Q L R代表询问你从第L支画笔到第R支画笔中共有几种不同颜色的画笔. ...
随机推荐
- App导航设计全面梳理——附免费原型模版!
生活中大家或多或少都会有迷路的经验,但你是不是从来没思考过迷路的定义是什么? 迷路的定义其实有两个核心: 1.想要到达一个目的地. 2.不知道自己在哪里,应该往哪走. 和生活中的迷路一样,我们在使用A ...
- Repeater 中TextBox 触发TextChanged事件
两种方法 1.TextBox 绑定TextChanged 并设置AutoPostBack ="true" ,如果不设置AutoPostBack ="true"则 ...
- 关于设置cookie同源,axios请求加上cookie
一个有cookie 一个没有 这是为啥!! axios都设置了的为true允许携带cookie 大佬答疑解惑:==>cookie同源域名才有啊,在Application看看cookie的pat ...
- 使用dynamic引发的异常:无法对 null 引用执行运行时绑定
今天上午运营反映有商户的账单没有生成. 查看日志,在批量生成账单服务执行过程中,因为如下异常而中断了: 跑批异常 Microsoft.CSharp.RuntimeBinder.RuntimeBinde ...
- 在屏幕拖拽3D物体移动
3D物体的拖拽不同于2D的.因为3D物体有x,y,z当然.实际拖拽还是在XZ平面.只是多了几个转换 using UnityEngine; using System.Collections; publi ...
- 数据加密之SymmetricAlgorithm加密
#region SymmetricAlgorithm加密 /// <summary> /// 按指定对称算法.键和向量加密字符串 /// </summary> public s ...
- 48.HTML---Flex 布局教程:实例篇
你会看到,不管是什么布局,Flex往往都可以几行命令搞定. 我只列出代码,详细的语法解释请查阅<Flex布局教程:语法篇>.我的主要参考资料是Landon Schropp的文章和Solve ...
- hbase-java-api002(flush)
package api; import java.io.IOException; import org.apache.hadoop.conf.Configuration; import org.apa ...
- Mysql 修改字段长度、修改列名、新增列、修改自增主键起始值
alter table 表名 modify column 字段名 类型; 例如 数据库中user表 name字段是varchar(30) 可以用 ) ; --修改字段长度 )--修改表列名 ); -- ...
- [17]Windows的启动过程
一.内核的引导 在intel x86系统上,windows操作系统获得控制首先从硬盘的主引导记录(MBR,Master Boot Record)开始,windows setup程序在安装windows ...