SVM数学原理推导

//2019.08.17

#支撑向量机SVM(Support Vector Machine)
1、支撑向量机SVM是一种非常重要和广泛的机器学习算法，它的算法出发点是尽可能找到最优的决策边界，使得模型的泛化能力尽可能地好，因此SVM对未来数据的预测也是更加准确的。

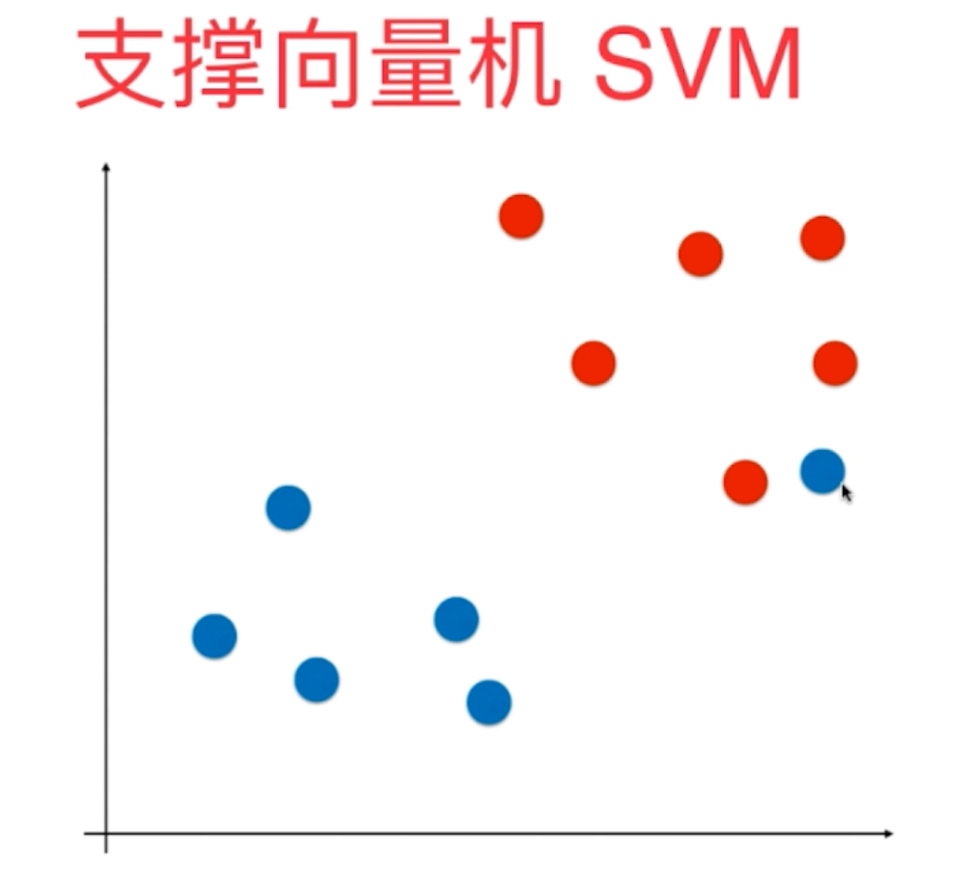
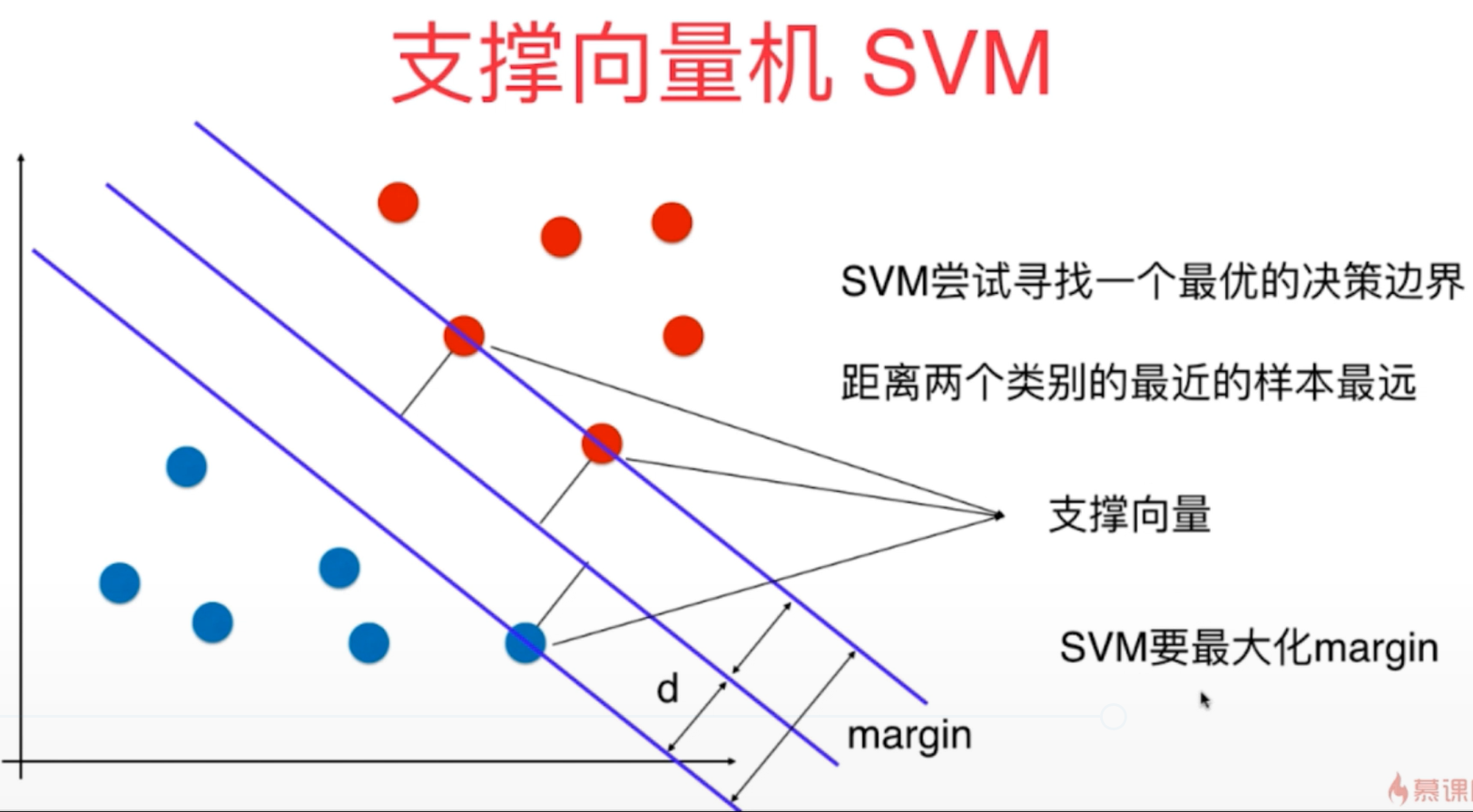
2、支撑向量机SVM有两种：Hard Margin SVM和Soft Margin SVM，对于第一种严格的支撑向量机算法主要解决的是线性可分的数据问题，而第二种SVM是在第一种的基础上改进而来，可以解决普遍的数据问题，对于问题的线性可分性没有特殊的要求。

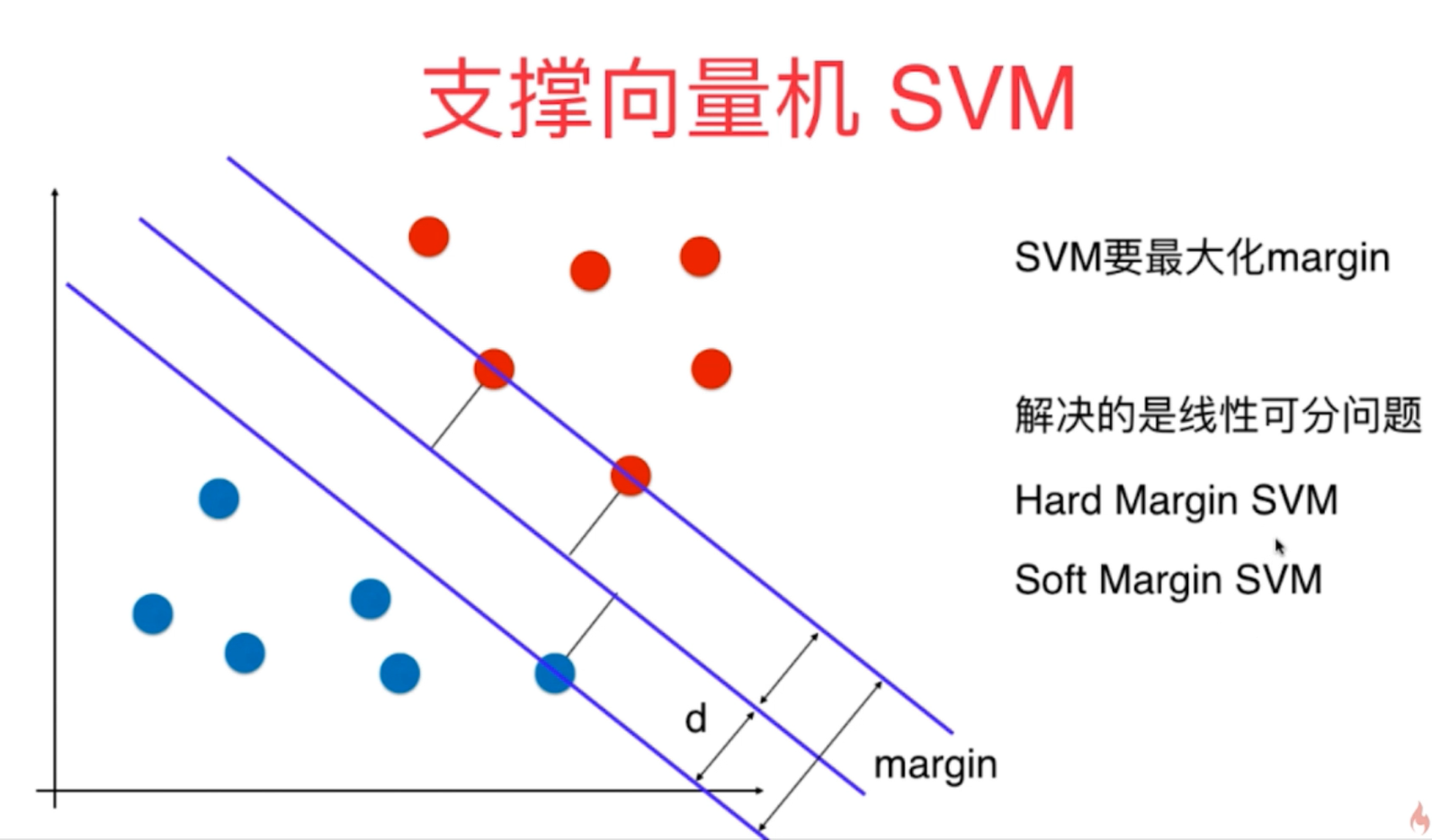
3、支持向量机线性可分算法数学原理最终推导的结果是求解有条件情况下的最优化问题，这种问题解决起来相对复杂，可以用拉普拉斯算子来进行解决。

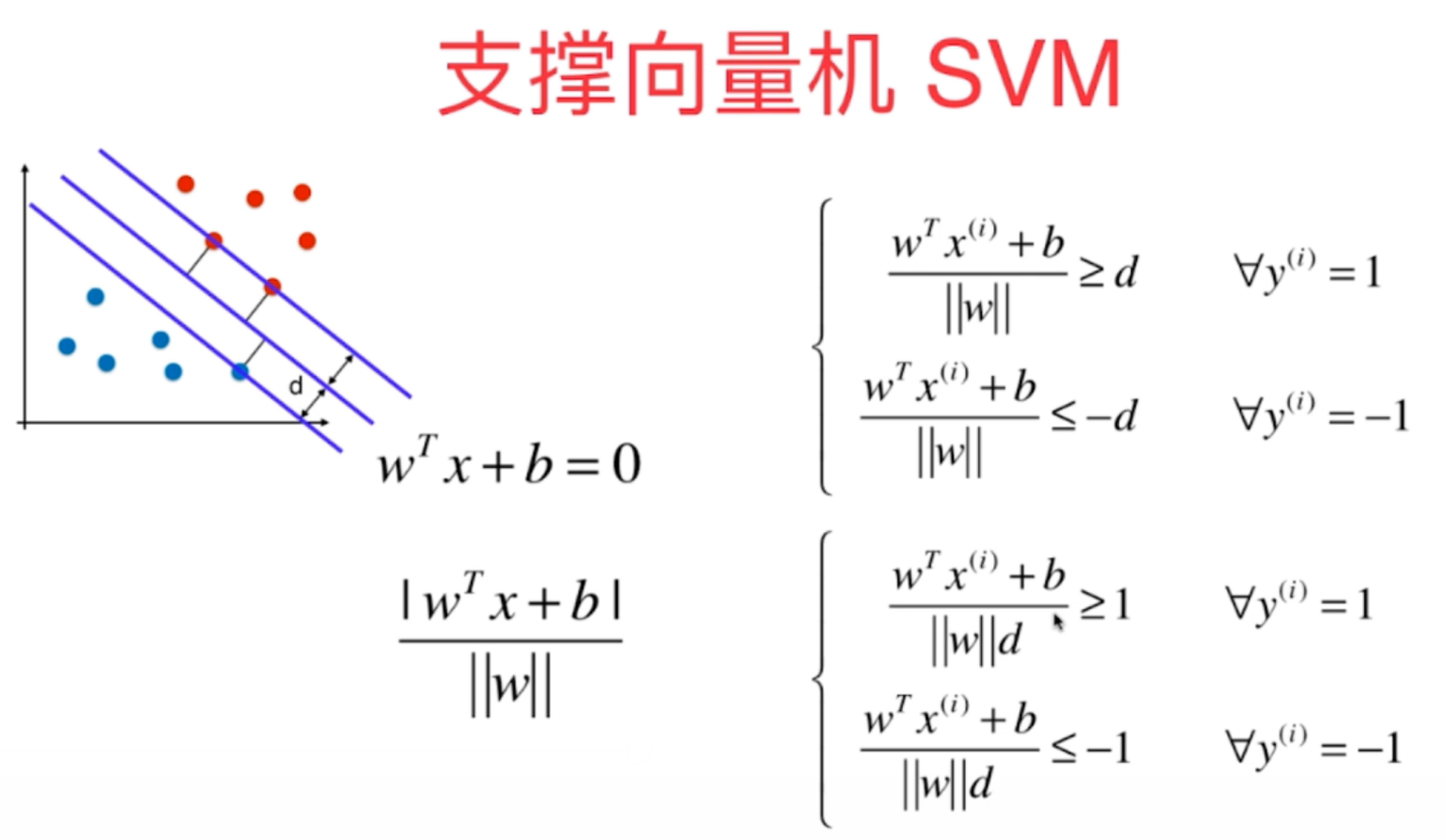
4、在sklearn中调用SVM算法时和KNN算法使用类似，需要先对数据进行标准化处理StandardScaler，因为它的数学原理也涉及到了距离，因此高维数据里面不同维度的数据尺度应该相当，相差太大会使得算法结果准确度降低。

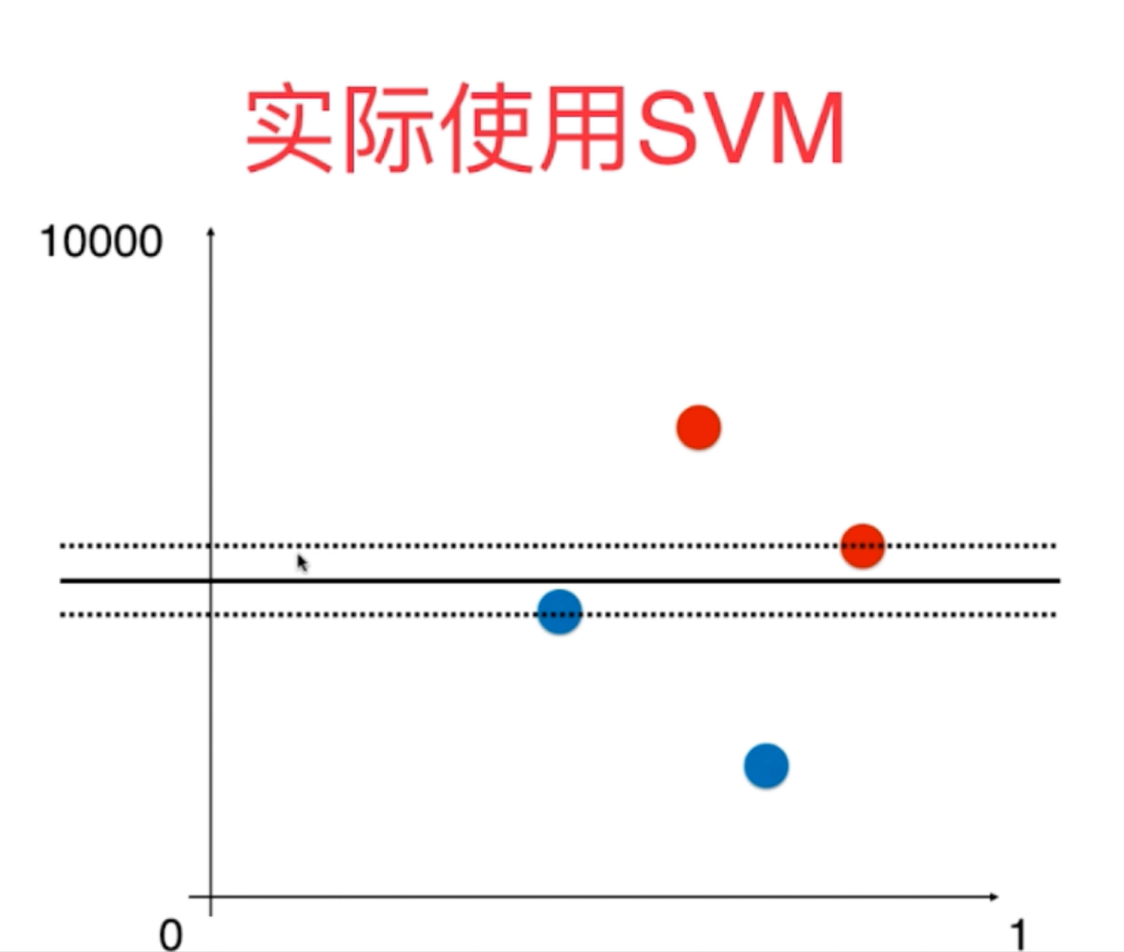
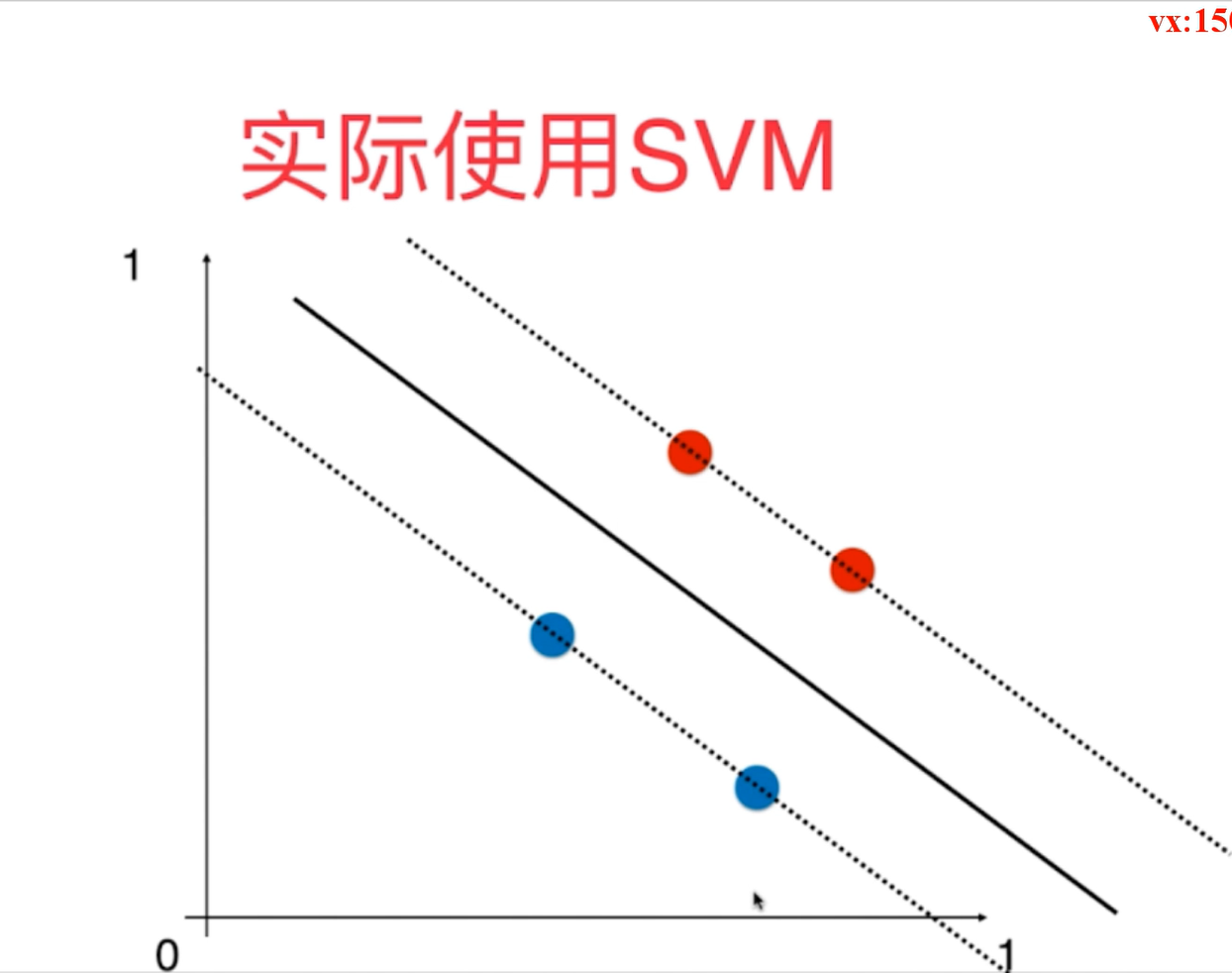
5、对于SVM算法，需要进行正则化，正则化的方式也有L1和L2正则化两种方式，引入了超参数C，使得模型有了一定的容错空间，这样使得模型的泛化能力得到了增强。C越小，其容错能力越高，如果C趋于无穷，则转换为了严格线性SVC。因此在调入SVM算法时需要定义三大参数：C(正则化系数、penalty=l1/l2正则化方式以及multi_class=ovr/ovo多分类的方式)

6、sklearn中调用多项式的SVM算法主要有两种方式：
(1)利用管道pipeline常规的方式进行：多项式特征添加，数据标准化以及SVM算法
(2)利用SVM自带的多项式核函数svm算法直接进行训练，这列需要定义很重要的参数kernel="poly"，它表示多项式形式的SVM算法。
7、SVC算法的数学原理是求取一定条件下的最优化函数，经过一定的数学公式转换，便可以转换为另外一种等效的最优化问题，对于等效之后的求取最优化函数中带有Xi.Xj这样的式子，这是两个数据样本向量之间的点乘，对于只要有这样式子的函数，我们都可以引入核函数K(x,y)，使得具有一定的特殊特征,具体的数学原理如下所示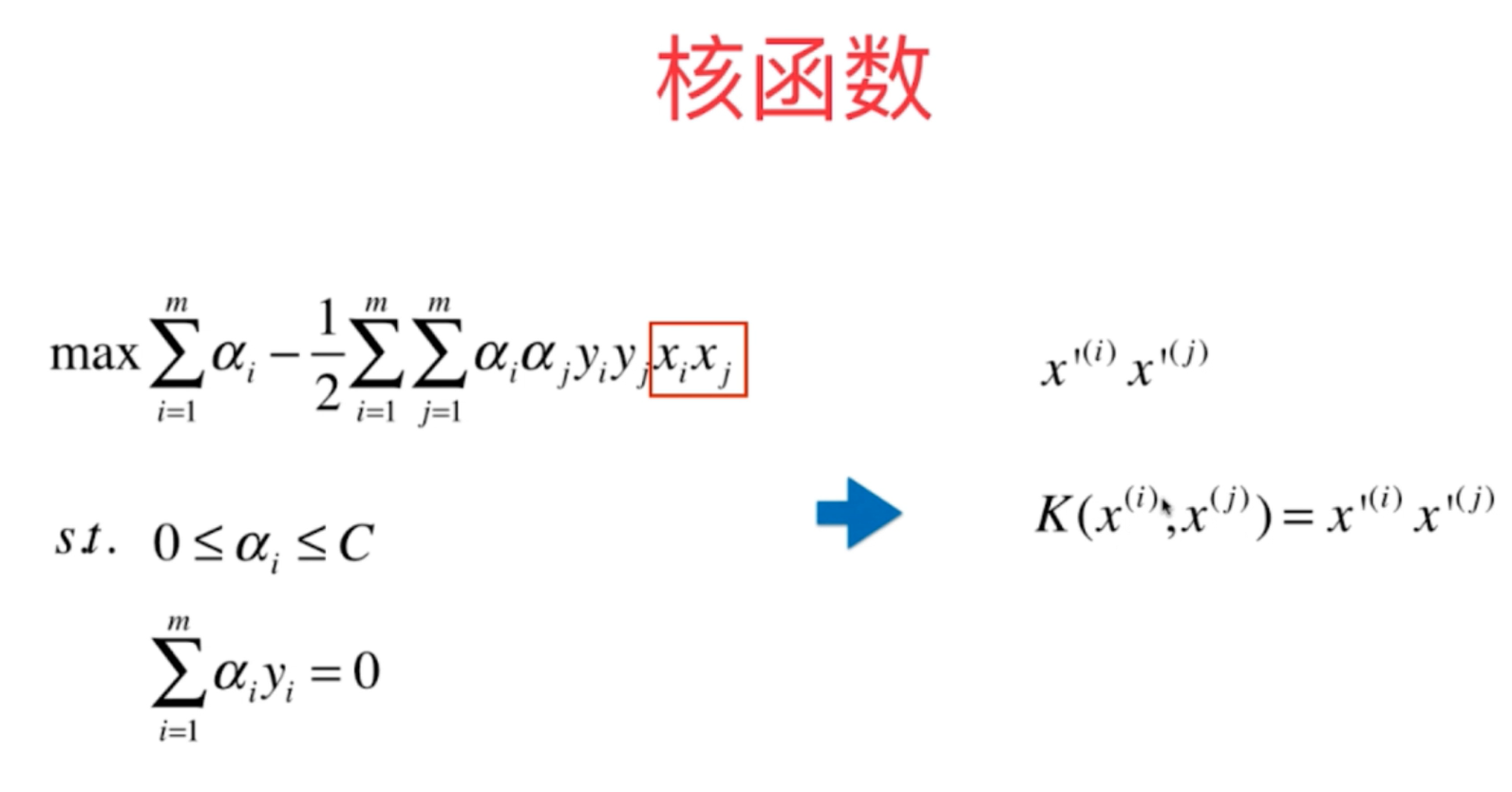

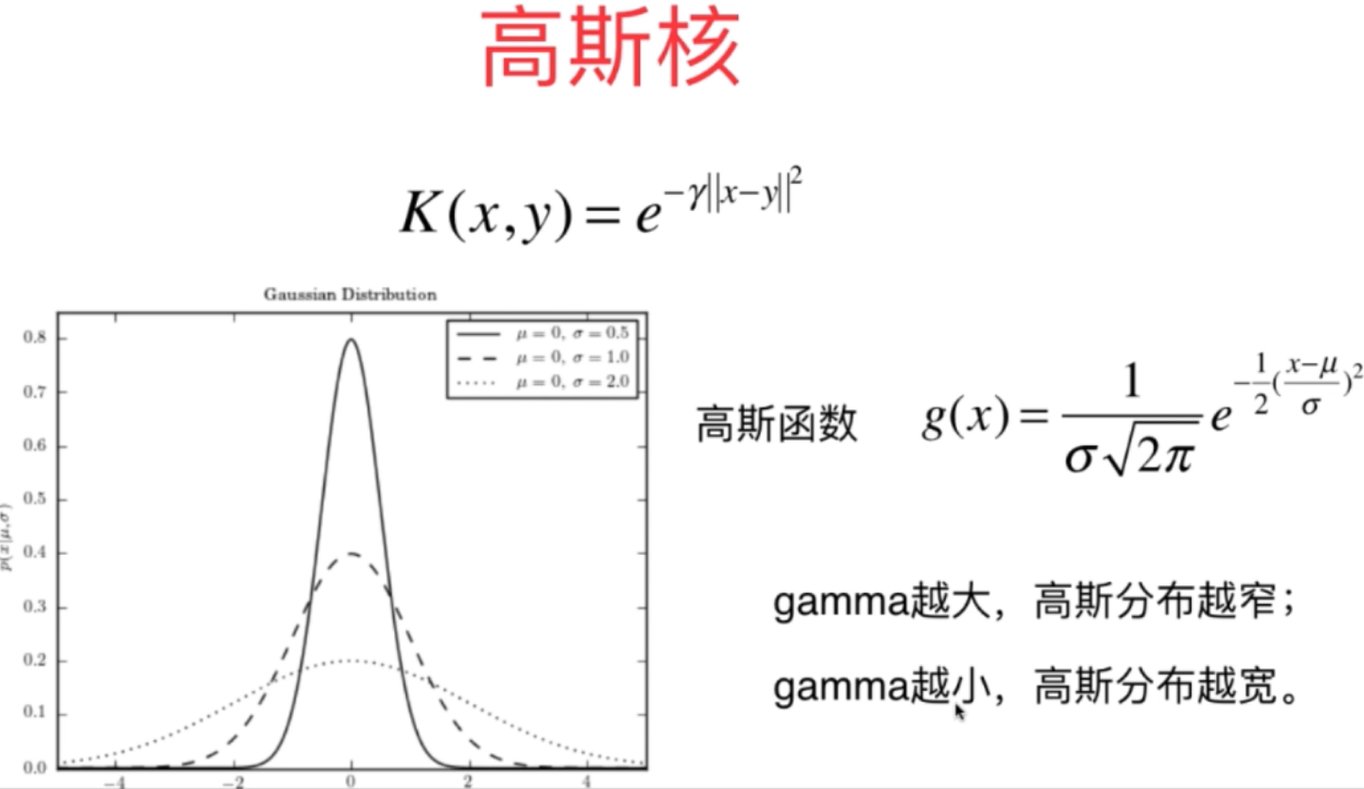
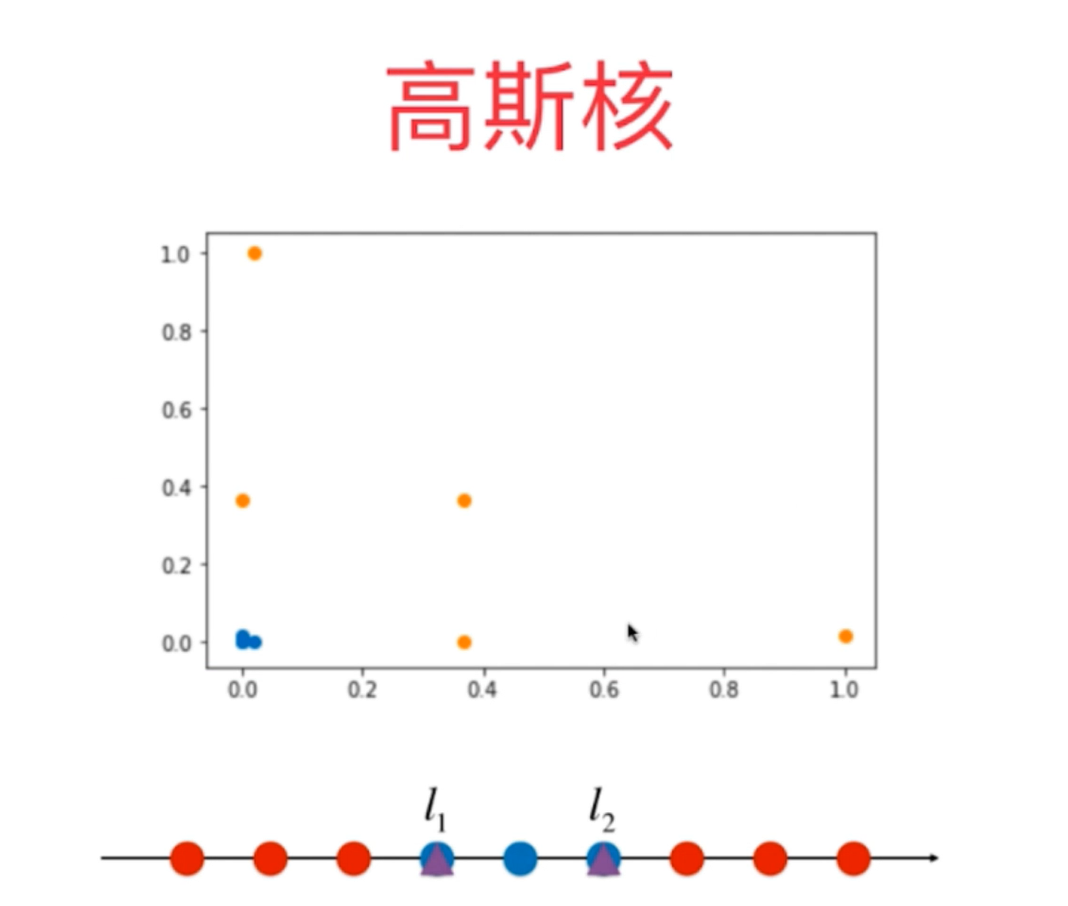
8、对于SVM的高斯核函数是一种比较特殊又功能强大的核函数，它可以将数据样本从mxn升维到mxm的数据，所以它的训练时间还是比较长的。对于高斯核函数的应用，一般用在数据集特点是m<n的基础数据集，即数据维度非常高的数据。