POJ2942 UVA1364 Knights of the Round Table 圆桌骑士

POJ2942 洛谷UVA1364（博主没有翻墙uva实在是太慢了）

以骑士为结点建立无向图，两个骑士间存在边表示两个骑士可以相邻（用邻接矩阵存图，初始化全为1，读入一对憎恨关系就删去一条边即可），则题意变为求图中不在任何奇环（结点数为奇数的环）中的点的数量。

一个环上的点一定属于一个双连通分量（两两都有两条路径可达）

那么什么时候双连通分量中没有奇环呢？

显然，当双连通分量是二分图的时候，图中没有奇环，因为从一个点出发回到该点一定要经过偶数条边。

即非二分图的双连通分量一定含有奇环

那么，非二分图的双连通分量的每个点是否都在奇环中呢？

假设v,u1,u2属于同一个双连通分量，且已知u1,u2在奇环上。求证：v也在奇环上

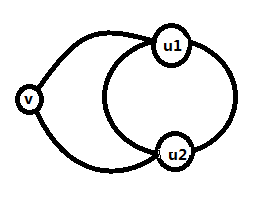
因为u1,u2在奇环上，所以u1,u2在环上的两条路径一条长度为奇数，一条长度为偶数。故无论u1-v-u2的长度为奇数或偶数都可以以v,u1,u2构造一个奇圈

所以我们得到非二分图的双连通分量中的每个点都在奇环上

那么我们的任务就转换为求无向图中是二分图的双连通分量中点的个数

有了上面的分析，代码实现就很简单了

 #include<cstdio>
 #include<cctype>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 #define re register int
 int graph[][];//邻接矩阵
 int dfn[],dfs_clock,n,m,stack[],top,ans,queue[],left,right,color[];
 int bccno[],bcc_cnt,tot;//各个点bcc编号、当前bcc编号、bcc结点数目
 bool odd[];//每个点是否在奇圈上
 int read()
 {
     int f=,x=;
     char c=getchar();
     while(!isdigit(c))
     {
         f=f|c=='-';
         c=getchar();
     }
     while(isdigit(c))
     {
         x=(x<<)+(x<<)+(c^);
         c=getchar();
     }
     return x;
 }
 bool bipartite(int x)//二分图判定
 {
     memset(color,,sizeof(color));
     left=right=;
     queue[]=x;
     color[x]=;
     while(right>=left)
     {
         int u=queue[left++];
         for(re v=;v<=n;v++)
         {
             if(graph[u][v]&&bccno[v]==bcc_cnt)
             {
                 if(color[v]==color[u])
                     return false;
                 else if(!color[v])
                 {
                     queue[++right]=v;
                     color[v]=^color[u];
                 }
             }
         }
     }
     return true;
 }
 int tarjan(int u,int fa)//求双连通分量
 {
     int lowu=dfn[u]=++dfs_clock;
     for(re v=;v<=n;v++)
         if(graph[u][v])
         {
             if(!dfn[v])
             {
                 stack[++top]=v;
                 int lowv=tarjan(v,u);
                 lowu=min(lowu,lowv);
                 if(lowv>=dfn[u])
                 {
                     tot=;
                     bcc_cnt++;
                     while(stack[top]!=v)
                     {
                         tot++;
                         bccno[stack[top--]]=bcc_cnt;
                     }
                     tot+=;
                     bccno[stack[top--]]=bccno[u]=bcc_cnt;//割点不出栈
                     if(!bipartite(u))//不是二分图，则此BCC中的点均在奇圈上
                         for(re i=;i<=n;i++)
                             if(bccno[i]==bcc_cnt)
                                 odd[i]=true;
                 }
             }
             else if(v!=fa)
                 lowu=min(lowu,dfn[v]);
         }
     return lowu;
 }
 void reset()
 {
     memset(bccno,,sizeof(bccno));
     memset(dfn,,sizeof(dfn));
     memset(odd,,sizeof(odd));
     dfs_clock=bcc_cnt=ans=top=;
     for(re i=;i<=n;i++)
         for(re j=;j<=n;j++)
             graph[i][j]=;
     for(re i=;i<=n;i++)
         graph[i][i]=;
 }
 int main()
 {
     while((n=read())&&(m=read()))
     {
         reset();
         while(m--)
         {
             int u=read(),v=read();
             graph[u][v]=graph[v][u]=;
         }
         for(re i=;i<=n;i++)
             if(!dfn[i])
             {
                 stack[++top]=i;
                 tarjan(i,i);
             }
         for(re i=;i<=n;i++)
             if(!odd[i])
                 ans++;
         printf("%d\n",ans);
     }
     return ;
 }

Knights of the Round Table 圆桌骑士