一本通1635【例 5】Strange Way to Express Integers

1635：【例 5】Strange Way to Express Integers

sol：貌似就是曹冲养猪的加强版，初看感觉非常没有思路，经过一番艰辛的***，得到以下的结果

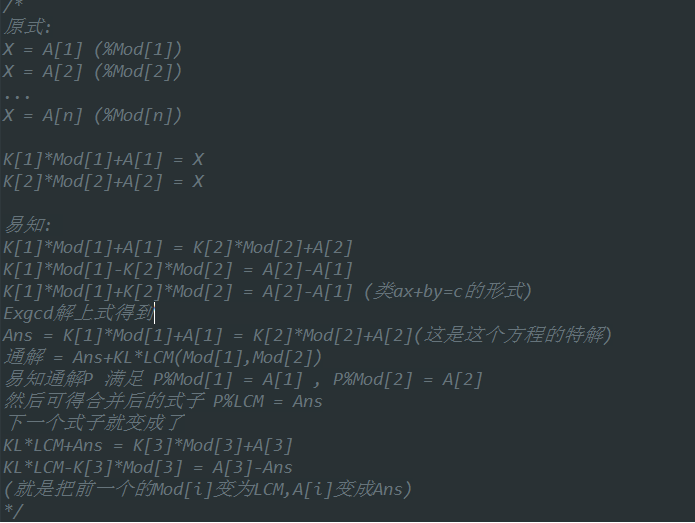
随便解释下给以后的自己听：K是要求的数字

第一个读入的A₁，Mod₁不用改，从2开始做，把Mod₂改成LCM，A₂改成Ans，接着搞3

/*
原式:
X = A[1] (%Mod[1])
X = A[2] (%Mod[2])
...
X = A[n] (%Mod[n])
 
K[1]*Mod[1]+A[1] = X
K[2]*Mod[2]+A[2] = X
 
易知:
K[1]*Mod[1]+A[1] = K[2]*Mod[2]+A[2]
K[1]*Mod[1]-K[2]*Mod[2] = A[2]-A[1]
K[1]*Mod[1]+K[2]*Mod[2] = A[2]-A[1] (类ax+by=c的形式)
Exgcd解上式得到
Ans = K[1]*Mod[1]+A[1] = K[2]*Mod[2]+A[2](这是这个方程的特解)
通解 = Ans+KL*LCM(Mod[1],Mod[2])
易知通解P 满足 P%Mod[1] = A[1] , P%Mod[2] = A[2]
然后可得合并后的式子 P%LCM = Ans
下一个式子就变成了
KL*LCM+Ans = K[3]*Mod[3]+A[3]
KL*LCM-K[3]*Mod[3] = A[3]-Ans
(就是把前一个的Mod[i]变为LCM,A[i]变成Ans)
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll s=;
    bool f=;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<)+(s<<)+(ch^); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<)
    {
        putchar('-'); x=-x;
    }
    if(x<)
    {
        putchar(x+''); return;
    }
    write(x/);
    putchar((x%)+'');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const ll N=;
int n;
ll A[N],Mod[N];
inline ll gcd(ll x,ll y)
{
    return (!y)?(x):(gcd(y,x%y));
}
inline void Exgcd(ll a,ll b,ll &X,ll &Y)
{
    if(b==)
    {
        X=;
        Y=;
        return;
    }
    Exgcd(b,a%b,X,Y);
    ll XX=X,YY=Y;
    X=YY;
    Y=XX-a/b*YY;
    return;
}
inline ll Solve()
{
    int i;
    ll a,b,c,r,X,Y,LCM=Mod[],Ans=A[];
    for(i=;i<=n;i++)
    {
        a=Mod[i-];
        b=Mod[i];
        c=A[i]-A[i-];
        r=gcd(a,b);
        if(c%r) return -;
 
        Exgcd(a,b,X=,Y=);
        X=X*c/r;
        ll tmp=b/r;
        X=(X>=)?(X%tmp):(X%tmp+tmp);
 
        LCM=LCM*b/r;
        Mod[i]=LCM;
        Ans=X*Mod[i-]+A[i-];
        Ans%=LCM;
        A[i]=Ans;
    }
    return Ans;
}
int main()
{
//    freopen("2.in","r",stdin);
//    freopen("my.out","w",stdout);
    int i;
    while(~scanf("%d",&n))
    {
        for(i=;i<=n;i++)
        {
            R(Mod[i]); R(A[i]);
        }
        Wl(Solve());
    }
    return ;
}
/*
input
2
8 7
11 9
output
31
 
input
3
91 26
62 49
95 80
3
23 9
89 80
72 15
output
409435
36303
*/