【LGR-065】洛谷11月月赛 III Div.1

T1,T2,T3,T4

---

T1 基础博弈练习题

分析

首先区间长度为1的情况特判，偶数必胜，奇数必败

考虑倒推，如果最后一个位置为偶数那么该位置为必败局面，否则为必胜局面

因为先手到这个位置要减去1就会让后手为偶数就赢了

那么如果是偶数显然不能走这一格，奇数那么前\(m-1\)个位置都是必败局面

可以从该位置向第一个必胜局面连边（前驱），

如果\([l\sim r]\)中\(l\)必然会到\(r\)（不然后手可以通过其它方式必胜）

也就是\(r\)在\(l\)的子树内时才会必胜

那么可以用dfs序\(O(n)\)预处理

---

代码

#include <cstdio>
#include <cctype>
#include <cstring>
#define rr register
using namespace std;
const int N=1000011;
struct node{int y,next;}e[N];
int A,B,C,P,n,m,Q,typ,dfn[N],Fa[N],tot,k,as[N],rfn[N],a[N];
inline signed iut(){
	rr int ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline void add(int x,int y){e[++k]=(node){y,as[x]},as[x]=k;}
inline signed rnd(){return A=(A*B+C)%P;}
inline void dfs(int x){
	dfn[x]=++tot;
	for (rr int i=as[x];~i;i=e[i].next)
	    dfs(e[i].y);
	rfn[x]=tot;
}
signed main(){
	memset(as,-1,sizeof(as));
	n=iut(),m=iut(),Q=iut(),typ=iut();
	for (rr int i=1;i<=n;++i) a[i]=iut();
	if (typ) A=iut(),B=iut(),C=iut(),P=iut();
	for (rr int i=1;i<=n;++i){
		rr int Le=i>m?i-m-1:0;
		if (a[i]&1){
			if (a[Le]&1) Fa[i]=Le,add(Le,i);//两个位置都是奇数必胜
			    else Fa[i]=Fa[Le],add(Fa[Le],i);//找到这个点的前驱
		}else{
			if (a[i-1]&1) Fa[i]=i-1,add(i-1,i);//直接连上一个位置
			    else Fa[i]=Fa[i-1],add(Fa[i-1],i);//同理
		}
	}
	dfs(0);
	rr unsigned sum=0,ans=0;
	for (rr int i=1,l,r;i<=Q;++i){
		sum+=i+i-1;
		if (typ){
			l=rnd()%n+1,r=rnd()%n+1;
		    if (l>r) l^=r,r^=l,l^=r;
		}else l=iut(),r=iut();
		if (l==r) ans+=a[l]&1?0:sum;
		else if (dfn[l]>dfn[r]||dfn[r]>rfn[l])
		    ans+=sum;
	}
	return !printf("%u",ans);
}

---

T2 基础最优化练习题

分析

贪心，对于\(w\)是负数，肯定要选择减\(k\)，因为减\(k\)不会影响以后的限制

如果是正数，还要考虑限制，首先先加上\(k\)，然后如果超过限制往当前\(a_i\)移动，

首先最多可以减\(2k\)，然后我肯定要选\(w\)最小的位置，那可以用堆处理，

找出\(w\)最小的位置，提取它能减小的次数，把答案减小，如果次数还有重新放回堆里，时间复杂度\(O(nlogn)\)

---

代码

#include <cstdio>
#include <cctype>
#include <algorithm>
#define rr register
using namespace std;
typedef long long lll;
const int N=1000011;
struct rec{
	lll w; int c;
	bool operator <(const rec &t)const{
	    return w<t.w;
	}
}heap[N];
int a[N],n,k,now,cnt; lll w[N],ans;
inline signed iut(){
	rr int ans=0,f=1; rr char c=getchar();
	while (!isdigit(c)) f=(c=='-')?-f:f,c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans*f;
}
inline void Push(rec w){
    heap[++cnt]=w;
    rr int x=cnt;
    while (x>1){
        if (heap[x]<heap[x>>1])
            swap(heap[x>>1],heap[x]),x>>=1;
        else return;
    }
}
inline void Pop(){
    heap[1]=heap[cnt--];
    rr int x=1;
    while ((x<<1)<=cnt){
        rr int y=x<<1;
        if (y<cnt&&heap[y+1]<heap[y]) ++y;
        if (heap[y]<heap[x]) swap(heap[y],heap[x]),x=y;
            else return;
    }
}
signed main(){
	n=iut(),k=iut();
	for (rr int i=1;i<=n;++i) a[i]=iut();
	for (rr int i=1;i<=n;++i) w[i]=iut();
	for (rr int i=n-1;i;--i) w[i]+=w[i+1];
	for (rr int i=1;i<=n;++i){
		if (w[i]>0) ans+=w[i]*k,now+=k,Push((rec){w[i],k<<1});
		    else ans-=w[i]*k,now-=k;
		while (now>a[i]){
			rr rec t=heap[1]; Pop();
			rr int less=min(now-a[i],t.c);
			ans-=less*t.w,now-=less;
			if (less<t.c) Push((rec){t.w,t.c-less});
		}
	}
	return !printf("%lld",ans);
}

---

T3 基础函数练习题

分析

如果学过笛卡尔树就知道要建一棵笛卡尔树（\(O(n)\)单调栈）

等于说两头往它们的LCA跳，分别处理，以左端点为例



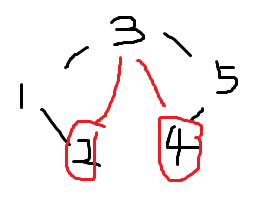
如果处理2~4，红色边才是应该找的，假设搜索到点\(x\)

这需要对之前的倍增数组有修改，比如说准备访问右端点时，父亲应该定为该点的父亲。

需要预处理\(x\)到\(f[x][i]\)的\(w\)总和（常规操作）和

\(f[x][i]\)的子树\(w\)总和（不包括\(x\)的左子树,右端点为右子树）（避免算重）

然后倍增的道理就是拼凑结果，也没有什么好说的了

可惜O2MLE了（常数小内存大直接暴毙）

---

代码

#include <cstdio>
#include <cctype>
#include <cmath>
#include <cstring>
#define rr register
using namespace std;
typedef long long lll;
const int N=500011;
lll s[N],ans[N],lin[N][19],sub[N][19];
int root,Lc[N],Rc[N],bas,w[N],f[N][19];
int a[N],n,Q,dep[N],B,l[N],r[N],LCA[N],st[N];
inline signed iut(){
	rr int ans=0,f=1; rr char c=getchar();
	while (!isdigit(c)) f=(c=='-')?-f:f,c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans*f;
}
inline void print(lll ans){
	if (ans>9) print(ans/10);
	putchar(ans%10+48);
}
inline lll max(lll a,lll b){return a>b?a:b;}
inline signed DiKaEr(){
	rr int top=0; a[0]=2e9;
	for (rr int i=1;i<=n;++i) a[i]=iut();
	for (rr int i=1,lst=0;i<=n;++i){
		while (a[st[top]]<a[i]) --top;
		if (top<lst) Lc[i]=st[top+1];
		if (top) Rc[st[top]]=i;
		st[lst=++top]=i;
	}
	for (rr int i=0;i<=n;++i) a[i]=0;
	for (rr int i=1;i<=n;++i) a[Lc[i]]=a[Rc[i]]=1;
	for (rr int i=1;i<=n;++i) if (!a[i]) return i;
	return 0;
}
inline void dfs1(int x,int fa){
	dep[x]=dep[fa]+1,f[x][0]=fa;
	for (rr int i=0;i<B&&f[x][i];++i)
		f[x][i+1]=f[f[x][i]][i];
	if (Lc[x]) dfs1(Lc[x],x);
	if (Rc[x]) dfs1(Rc[x],x);
	s[x]=max(s[Lc[x]],s[Rc[x]])+w[x];
}
inline signed lca(int x,int y){
	if (dep[x]<dep[y]) x^=y,y^=x,x^=y;
	for (rr int i=B;~i;--i)
	if (dep[f[x][i]]>=dep[y]) x=f[x][i];
	if (x==y) return x;
	for (rr int i=B;~i;--i)
	if (f[x][i]!=f[y][i])
	    x=f[x][i],y=f[y][i];
	return f[x][0];
}
inline void dfs2(int x,bool z){
	lin[x][0]=w[x],sub[x][0]=w[x]+(z?s[Lc[x]]:s[Rc[x]]);
	for (rr int i=0;i<B&&f[x][i];++i){
		f[x][i+1]=f[f[x][i]][i],lin[x][i+1]=lin[x][i]+lin[f[x][i]][i],
		sub[x][i+1]=max(lin[f[x][i]][i]+sub[x][i],sub[f[x][i]][i]);
	}
	if (Lc[x]) f[Lc[x]][0]=z?f[x][0]:x,dfs2(Lc[x],z);
	if (Rc[x]) f[Rc[x]][0]=z?x:f[x][0],dfs2(Rc[x],z);
}
inline lll query(int x,int y){
	rr lll ans=0;
	for (rr int i=B;~i;--i)
	if (dep[f[x][i]]>=dep[y]){
		ans=max(ans+lin[x][i],sub[x][i]);
		x=f[x][i];
	}
	return ans;
}
signed main(){
	n=iut(),Q=iut(),root=DiKaEr(); for (B=0;(2<<B)<=n;++B);
	for (rr int i=1;i<=n;++i) w[i]=iut(); dfs1(root,0);
	for (rr int i=1;i<=Q;++i) l[i]=iut(),r[i]=iut();
	for (rr int i=1;i<=Q;++i) LCA[i]=lca(l[i],r[i]);
	for (rr int i=1;i<=Q;++i) ans[i]=-1e16;
	memset(f,0,sizeof(f)),dfs2(root,0);
	for (rr int i=1;i<=Q;++i) ans[i]=max(ans[i],query(l[i],LCA[i])+w[LCA[i]]);
	memset(f,0,sizeof(f)),dfs2(root,1);
	for (rr int i=1;i<=Q;++i) ans[i]=max(ans[i],query(r[i],LCA[i])+w[LCA[i]]);
    for (rr int i=1;i<=Q;++i){
    	if (ans[i]<0) putchar('-'),ans[i]=-ans[i];
	    print(ans[i]),putchar(10);
	}
    return 0;
}

---

T4 基础数论函数题

分析

求区间LCM对\(10^9+7\)取模，多组数据多组询问,

\(n,T,Q\leq 300,a\leq 2^{60}\)

---

分析

首先\(2^{60}\)不能接受，因为除法和取模存在冲突，这就要求没有除法

那可以将LCM转换为区间积，也就是用当前数剔除之前存在的GCD，

那么就可以获得\(O(Tqn^2)\)的代码，把在线换成离线分治，时间复杂度是\(O(Tn^2)\)

回过头看一下怎样剔除GCD，可以用取模的方式实现

至于为什么没有\(GCD\)的常数，给出一部分代码就知道了

for (int j=mid+1;j<=r;++j) c[j]=mul(c[j-1],b[j],b[i]);//在后半部分剔除b[i]的约数
lll GCD=gcd(c[r],b[i]);//gcd(b[i],b[mid+1]*b[mid+2]*...*b[r-1]*b[r])
for (int j=r-1;j>=mid;--j)
if (c[j]%GCD){//gcd(b[j+1],GCD)必然不等于1
    lll Gcd=gcd(c[j],GCD);
    b[j+1]=b[j+1]/(GCD/Gcd),GCD=Gcd;//消约数
}
显然只有log个位置会被算上

---

代码

#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
typedef long long lll;
const lll mod=1000000007;
lll a[301],b[301],c[301];
int ans[301][301],n,Q;
inline lll iut(){
	rr lll ans=0; rr char c=getchar();
	while (!isdigit(c)) c=getchar();
	while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
	return ans;
}
inline lll gcd(lll a,lll b){return b?gcd(b,a%b):a;}
inline lll mul(lll a,lll b,lll mod){
	a=a%mod,b=b%mod;
	rr lll t=(long double)a*b/mod,ans=a*b-t*mod;
	ans=ans<0?ans+mod:ans,ans=ans>=mod?ans-mod:ans;
    return ans;
}
inline void print(int ans){
	if (ans>9) print(ans/10);
	putchar(ans%10+48);
}
inline void divi(int l,int r){
	if (l==r){
		ans[l][r]=a[l]%mod;
		return;
	}
	rr int mid=(l+r)>>1;
	divi(l,mid),divi(mid+1,r);
	rr lll t,t1=1,t2=1;
	for (rr int i=mid;i>=l;--i){
		b[i]=a[i],t=1;
		for (rr int j=i+1;j<=mid;++j)
		    t=mul(t,b[j],b[i]);
		b[i]=b[i]/gcd(b[i],t);
	}
	for (rr int i=mid+1;i<=r;++i){
		b[i]=a[i],t=1;
		for (rr int j=i-1;j>mid;--j)
		    t=mul(t,b[j],b[i]);
		b[i]=b[i]/gcd(b[i],t);
	}
	for (rr int i=mid;i>=l;--i){
		t2=t1=b[i]%mod*t1%mod,c[mid]=1;
		for (rr int j=mid+1;j<=r;++j)
		    c[j]=mul(c[j-1],b[j],b[i]);
		rr lll GCD=gcd(c[r],b[i]);
		for (rr int j=r-1;j>=mid;--j)
		if (c[j]%GCD){
			rr lll Gcd=gcd(c[j],GCD);
			b[j+1]=b[j+1]/(GCD/Gcd),GCD=Gcd;
		}
		for (rr int j=mid+1;j<=r;++j)
		    t2=ans[i][j]=b[j]%mod*t2%mod;
	}
}
signed main(){
	for (rr int Test=iut();Test;--Test){
		n=iut(),Q=iut();
		for (rr int i=1;i<=n;++i) a[i]=iut();
		divi(1,n);
		for (rr int l,r;Q;--Q,putchar(10))
		    l=iut(),r=iut(),print(ans[l][r]);
	}
	return 0;
}