洛谷P1004

洛谷P1004方格取数

题目大意

本题简要意思就是一个人从一个数字矩阵的左上角走到右下角，只能向下和向右走，拿完的数对应位置变成0，并且这个人要走两次，需要计算两次所拿数的最大值

Train of thought

本题和数字三角形十分类似，只不过要走两次，我们可以考虑用dp的方式解决问题

动态规划的关键是状态表示和递推方程

如果我们这里和数字三角形一样采用二维的dp方式，我们还需要找到所有第一次走的解，并且还要保存，然后在第一次解的角度上解析第二次走的收益

如图所示：

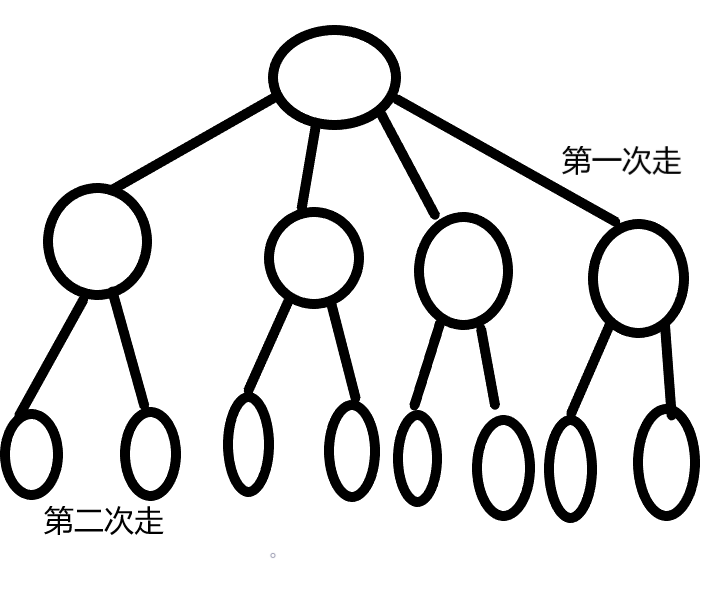
如果这样做的话时间复杂度可能是指数级别的，可能会超时

---

所以我们这里选择利用四维数组储存两次走的状态，f[i][j][k][l]表示第一次走到(k,l)，第二次走到(i,j)时所能得到的最大收益。

这里没有区分次序，对于可能出现的重复拿数的问题，我们需要把这个数减去

< if(i == k && j ==l) f[i][j][k][l] -= Square[i][j];>

递推方程显然为max(f[i-1][j][k-1][l],f[i - 1][j][k][l - 1],f[i][j- 1][k- 1][l],f[i][j-1][k][l-1])

也就是< f[i][j][k][l] = max(max(f[i - 1][j][k - 1][l],f[i - 1][j][k][l - 1]), max(f[i][j - 1][k - 1][l],f[i][j - 1][k][l - 1])) + Square[i][j] + Square[k][l];>

---

Time complexity

输入时最多有9^{2个数，处理时要处理9}4次，所以总的时间复杂度为9⁴⁺⁹2次

综上所述，代码如下：

#include<iostream>
#include<utility>
using namespace std;
typedef long long ll;
#define fi(a,b) for(int i = a; i <= b; ++i)
#define fr(a,b) for(int i = a; i >= b; --i)
using pii = pair<int,int>;
int Square[10][10];
int f[10][10][10][10];//数组表示的状态数
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
int a,b,c;
while(cin >> a >> b >> c && a && b && c)
Square[a][b] = c;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n ; ++j)
for(int k = 1; k <= n; ++k)
for(int l = 1; l <= n; ++l)
{
    f[i][j][k][l] = max(max(f[i - 1][j][k - 1][l],f[i - 1][j][k][l - 1]), max(f[i][j - 1][k - 1][l],f[i][j - 1][k][l - 1])) + Square[i][j] + Square[k][l];
    if(i == k && j ==l) f[i][j][k][l] -= Square[i][j];//避免重复拿数
}
cout << f[n][n][n][n] << endl;
return 0;
}

---

感谢大家的阅读，如果觉得还不错就点个赞吧ヾ(≧▽≦*)o