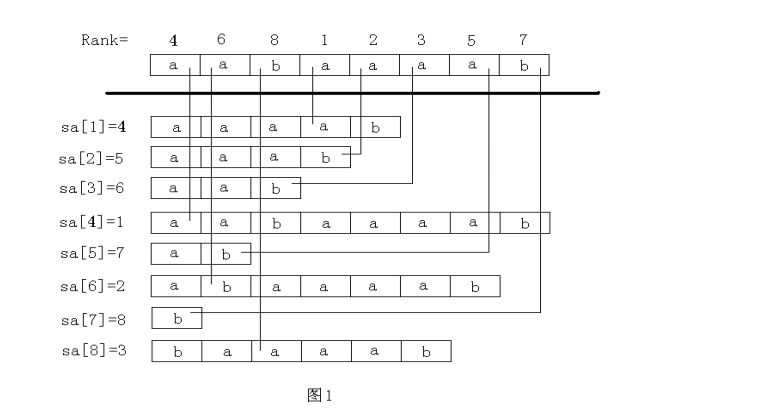
suffix array后缀数组

倍增算法

基本定义子串：字符串 S 的子串 r[i..j]，i≤j，表示 r 串中从 i 到 j 这一段
也就是顺次排列 r[i],r[i+1],...,r[j]形成的字符串。

后缀：后缀是指从某个位置 i 开始到整个串末尾结束的一个特殊子串。

字串 r 的 从 第 i 个 字 符 开 始 的 后 缀 表 示 为 Suffix(i) ， 也 就 是
Suffix(i)=r[i..len(r)]。

后缀数组：后缀数组 SA 是一个一维数组，它保存 1..n 的某个排列 SA[1]，
SA[2]，……，SA[n]，并且保证 Suffix(SA[i]) < Suffix(SA[i+1])，1≤i<n。
也就是将 S 的 n 个后缀从小到大进行排序之后把排好序的后缀的开头位置顺

次放入 SA 中。

名次数组：名次数组 Rank[i]保存的是 Suffix(i)在所有后缀中从小到大排
列的“名次”。
简单的说，后缀数组是“排第几的是谁？”，名次数组是“你排第几？”。容
易看出，后缀数组和名次数组为互逆运算。如图 1 所示。

设字符串的长度为 n。为了方便比较大小，可以在字符串后面添加一个字符,

这个字符没有在前面的字符中出现过，而且比前面的字符都要小。在求出名次数

组后，可以仅用 O(1)的时间比较任意两个后缀的大小。在求出后缀数组或名次
数组中的其中一个以后，便可以用 O(n)的时间求出另外一个。任意两个后缀如
果直接比较大小，最多需要比较字符 n 次，也就是说最迟在比较第 n 个字符时一
定能分出“胜负”。

1.2 倍增算法

倍增算法的主要思路是：用倍增的方法对每个字符开始的长度为 2k 的子字
符串进行排序，求出排名，即 rank 值。k 从 0 开始，每次加 1，当 2k 大于 n 以
后，每个字符开始的长度为 2k 的子字符串便相当于所有的后缀。并且这些子字
符串都一定已经比较出大小，即 rank 值中没有相同的值，那么此时的 rank 值就
是最后的结果。每一次排序都利用上次长度为 2k-1的字符串的 rank 值，那么长
度为 2k 的字符串就可以用两个长度为 2k-1的字符串的排名作为关键字表示，然
后进行基数排序，便得出了长度为 2k的字符串的 rank 值。以字符串“aabaaaab”
为例，整个过程如图 2 所示。其中 x、y 是表示长度为 2k的字符串的两个关键字

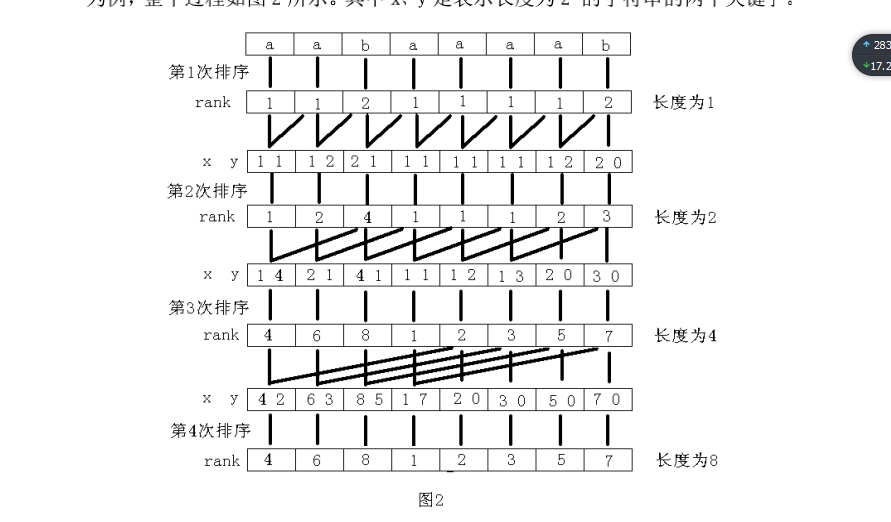
模板

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
#define rep(i,n) for(int i = 0;i < n; i++)
const int  maxn = 200000+66;
int rk[maxn],sa[maxn],height[maxn],w[maxn],wa[maxn],res[maxn];
void getSa (int len,int up) {
    int *k = rk,*id = height,*r = res, *cnt = wa;
    rep(i,up) cnt[i] = 0;
    rep(i,len) cnt[k[i] = w[i]]++;
    rep(i,up) cnt[i+1] += cnt[i];
    for(int i = len - 1; i >= 0; i--) {
        sa[--cnt[k[i]]] = i;
    }
    int d = 1,p = 0;
    while(p < len){
        for(int i = len - d; i < len; i++)
            id[p++] = i;
        rep(i,len)
        if(sa[i] >= d)
            id[p++] = sa[i] - d;
        rep(i,len) r[i] = k[id[i]];
        rep(i,up) cnt[i] = 0;
        rep(i,len) cnt[r[i]]++;
        rep(i,up) cnt[i+1] += cnt[i];
        for(int i = len - 1; i >= 0; i--) {
            sa[--cnt[r[i]]] = id[i];
        }
        swap(k,r);
        p = 0;
        k[sa[0]] = p++;
        rep(i,len-1) {
            if(sa[i]+d < len && sa[i+1]+d <len &&r[sa[i]] == r[sa[i+1]]&& r[sa[i]+d] == r[sa[i+1]+d])
                k[sa[i+1]] = p - 1;
            else k[sa[i+1]] = p++;
        }
        if(p >= len) return ;
        d *= 2,up = p, p = 0;
    }
}
int ans=0;
void getHeight(int len) {
    rep(i,len) rk[sa[i]] = i;
    height[0] = 0;
    for(int i = 0,p = 0; i < len - 1; i++) {
        int j = sa[rk[i]-1];
        while(i+p < len&& j+p < len&& w[i+p] == w[j+p]) {
            p++;
        }
        height[rk[i]] = p;
        p = max(0,p - 1);
    }
}
int getSuffix(char s[]) {
    int len = strlen(s),up = 0;
    for(int i = 0; i < len; i++) {
        w[i] = s[i];
        up = max(up,w[i]);
    }
    w[len++] = 0;
    getSa(len,up+1);
    getHeight(len);
    return len;
}

int main()
{
    char s1[maxn];
    scanf("%s",s1);

    getSuffix(s1);
    return 0;
}