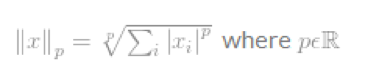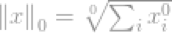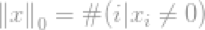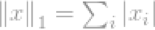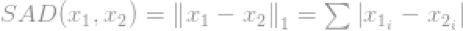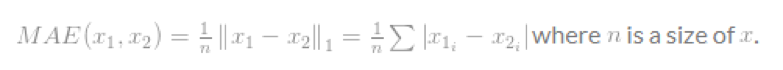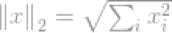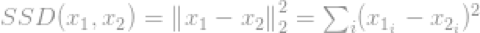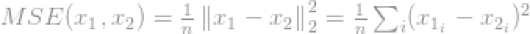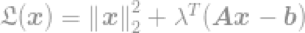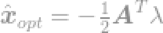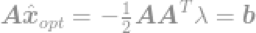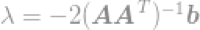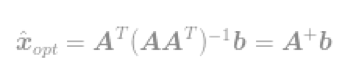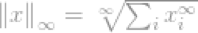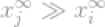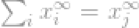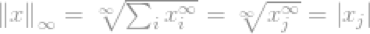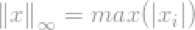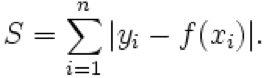L1正则和L2正则的比较分析详解

原文链接：https://blog.csdn.net/w5688414/article/details/78046960

范数(norm）

数学上，范数是一个向量空间或矩阵上所有向量的长度和大小的求和。简单一点，我们可以说范数越大，矩阵或者向量就越大。范数有许多种形式和名字，包括最常见的：欧几里得距离（Euclideandistance），最小均方误差（Mean-squared Error）等等。

大多数时间，你会在等式中看见范数像下面那样：
||x||,x可以是一个向量或者矩阵。
例如一个向量

其欧几里得范数为：

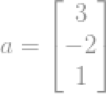
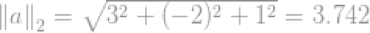
即向量a的模的大小。上面的例子展示了怎样计算欧几里得范数，或者叫做l2-norm.

X的Lp-norm的规范定义如下：

有趣的是，lp-norm看起来非常相似，但是他们的数学特性非常不同，结果应用场景也不一样。因此，这里详细介绍了几种范式。

L0-norm

我们需要讨论一下l0-norm，l0-norm的定义是：

严格的说，L0-norm不是一个真正的范数。它是一个基数函数（cardinalityfunction），有lp-norm的定义形式，这个式子有点特别，因为式子中有0的幂（zeroth-power）和0个根号（zeroth-root），显然，任何x>0，将会变为1.但是0的幂和0的开根号的定义很混乱。所以实际上，大多数数学家和工程师使用下面的l0-norm的定义：

即向量中非零元素的总个数。

由于它是非零元素的总数，因此有很多应用使用l0-norm。随后，由于压缩传感计划（Compressive Sensing
scheme）的发展，变得越来越重要。压缩传感计划试图找到欠定线性系统（under-determinedlinear
system）最稀疏的解（sparsest
solution）。最稀疏的解意味着解有最少的非零元素。即最少的l0-norm。这个问题通常被当做一个l0-norm优化问题

或者l0优化（optimisation）。

 

L0-optimisation

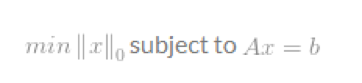
许多应用，包括压缩感知，试图最小化一个向量的l0-norm,这个向量有一些限制条件。因此叫做l0-minimisation.一个标准的最小化问题的定义为：

可是，优化上式不是一件容易的事。因为缺乏l0-norm的数学表示，l0-minimisation被计算机科学家认为是一个NP难问题（NP-hard problem），简单的说，它太复杂了，目前数学上没有求解办法。

在多数情况下，l0-minimisation问题都转换为高阶范数问题（higher-order norm problem），例如l1-minimisation和l2-minimisation.

L1-norm

 

X的l1-norm的定义为：

这个范数在范数家族中相当常见，它有很多名字和许多种形式，它的昵称是曼哈顿范数（Manhattannorm）。两个向量或矩阵的l1-norm为

在计算机视觉科学家眼中，它叫做绝对偏差和（Sum of AbsoluteDifference，SAD）。

在一般情况下，它可以用于一个单元的偏差计算：

它叫做均方绝对误差（Mean-Absolute Error，MAE）.

L2-norm

 

所有范数中最流行的是l2-norm。总体上，它用于工程和科学领域的方方面面。基本定义如下，l2-norm:

它的平方形式，在计算机视觉领域为平方差的和（Sumof Squared Difference，SSD）

它最出名的应用是在信号处理领域，为均方误差（Mean-SquaredError，MSE），它被用来计算两个信号的相似度，质量（quality）和关系。MSE为：

L2-optimisation

和l0-optimisation一样，最小化l2-norm的问题格式化定义为

假设限制矩阵A是全秩的，这个问题现在就是有无穷解的欠定系统（underderterminedsystem）。我们的目标是求出最优解，例如，求有最小l2-norm的解，如果直接计算的话，这会很麻烦。幸运的是它有一个数学技巧可以帮助我们求解。通过使用拉格朗日乘数（Lagrangemultipliers），我们可以定义一个拉格朗日乘子。

λ是引入的拉格朗日乘数。求导，然后等式等于0，我们可以找到一个最优解，因此得到

把解带入限定式中得到

最终

通过使用这个式子，我们可以立即求出l2-optimisation问题的最优解。这个等式因Moore-Penrose Pseudoinverse(读者自行百度，我也不知道，对不住了)而闻名，这个问题通常称为最小均方问题，最小均方回归或者最小均方优化。

可是，即使最小均方的方法很容易计算，但是计算的往往不是最好的解，这是因为l2-norm本身的平滑（曲线，处处可导）性质，很难找倒单个，适应问题的最佳解。

相反，l1-optimisation可以提供比这个解更好的结果。

L1-optimisation

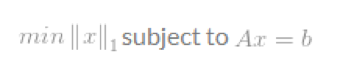
L1-optimisation问题的格式化定义为

由于l1-norm不像l2-norm那样光滑，问题的解就会比l2-optimisation更好更唯一.

可是，尽管l1-minimisation的问题几乎和l2-minimisation有相同的形式，但是也很难求解，因为问题没有一个平滑（有些地方不可导）的函数，我们用来解决l2-problem就不再适用

了。留下来的唯一方式是直接搜索，寻找解意味着我们的计算每一个我们找到的可能解，以找到找到最佳的那个解。

因为在数学上我们不能找到一个解决方法，l1-optimisation的实用性在过去几十年里是相当有限的。直到最近，具有高效计算能力的电脑可以使得我们找到每一个解。通过使用许多实用的算法，称为凸优化（ConvexOptimisation）算法，例如线性规划（linear
programming）或者非线性规划（non-linear programming）等等。

现在有许多关于l1-optimisation的toolboxes，这些toolboxes通常视同不同的方法或算法来解决同一个问题，toolboxes的样例为l1-magic,SparseLab,ISAL1.

L-infinity norm

l∞-norm的定义为

考虑向量x，如果xj是向量x中最高的条目，因为其无穷的属性，我们可以说

现在我们可以简单的说l∞-norm

这是向量最大条目的刻度。这显然不满足l∞-norm的意义

比较分析

当我们在做机器学习实践的时候，我们会迷茫是选择L1正则还是选择L2正则，因此我做了一下比较分析。

L1-norm(范数)，也叫作最小绝对偏差（leastabsolute deviations, LAD），最小绝对误差（least absolute errors，LAE）.它是最小化目标值yi和估计值f(xi)绝对差值的求和：

L2-norm(范数)也称为最小均方(least squares)，它是最小化目标值yi和估计值f(xi)平方和。
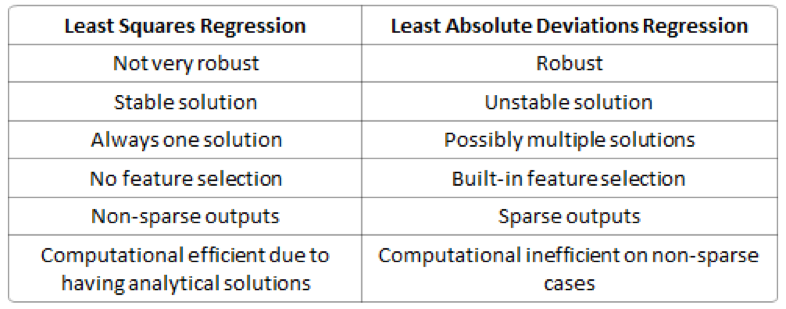
L1-norm和L2-norm的区别如下表格

鲁棒性（Robustness）：最小绝对值偏差的方法应用领域很广，相比最小均方的方法，它的鲁棒性更好，LAD能对数据中的异常点有很好的抗干扰能力，异常点可以安全的和高效的忽略，这对研究帮助很大。如果异常值对研究很重要，最小均方误差则是更好的选择。

对于L2-norm，由于是均方误差，如果误差>1的话，那么平方后，相比L-norm而言，误差就会被放大很多。因此模型会对样例更敏感。如果样例是一个异常值，模型会调整最小化异常值的情况，以牺牲其它更一般样例为代价，因为相比单个异常样例，那些一般的样例会得到更小的损失误差。

稳定性：LAD方法的不稳定属性意思是，对于一个书评调整的数据集，回归线可能会跳跃很大。这个方法对一些数据配置有连续的解决方法；可是，通过把数据集变小，LAD可以跳过一个有多个求解拓展区域的布局（one
could “jump past” a configurationwhich has multiple solutions that span
a
region，这句翻译挺麻烦的，大家自己领会吧，我尽力了），再通过这个解决方案的区域后，LAD线有一个斜坡，可能和之前的线完全不同。相比较之下，最小均方解决方法是稳定的，对于任何晓得数据点的调整，回归线仅仅只稍微移动一下，回归参数就是数据的连续函数（continuousfunctions
of the data）。

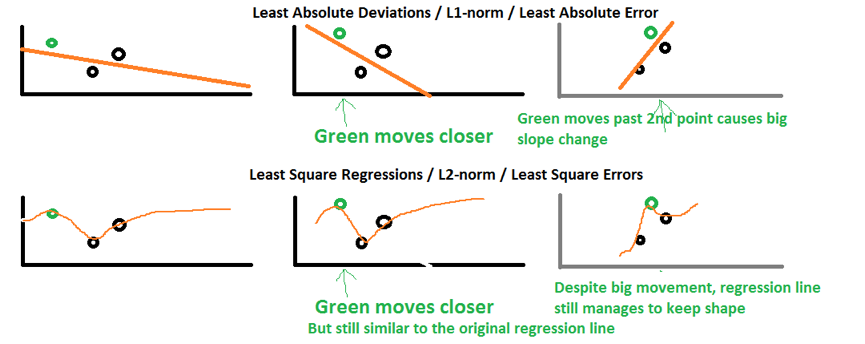
上图的上面代表的是L1-norm，底部代表的是L2-norm。第一列代表一个回归线怎样适应这三个点的。

假设我们把绿色的点视屏享有移动一点，L2-norm维持了和原回归线一样的形状，但是形成了更陡的抛物线（steeper parabolic
curve）。可是在L1-norm的样例中，回归线的斜率更陡了，并且影响到了其它点的预测值，因此，与L2-norm相比，所有的未来的预测都会都会受到影响。

假设我们把绿色的点水平向右移动得更远，L2-norm变化了一点，但是L1-norm变化更大了，l1-norm的斜率完全改变了。这种变化会使得所有以前的结果都不再合法（invalidate all previous results）。

数据点的稍稍调整，回归线就会变化很多，这就是L1-norm的不稳定性的表现之处。

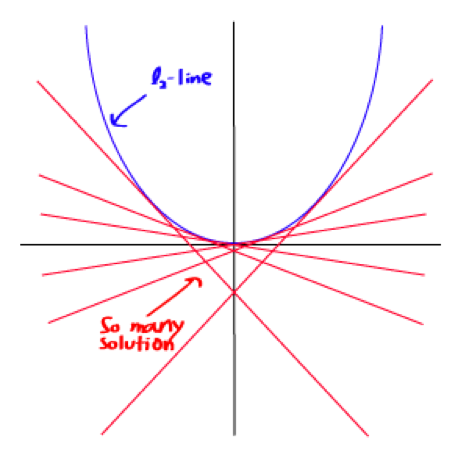
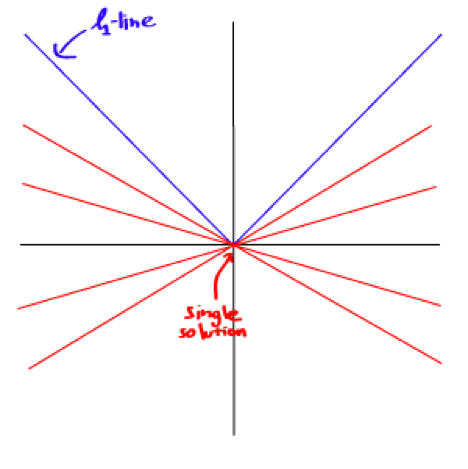
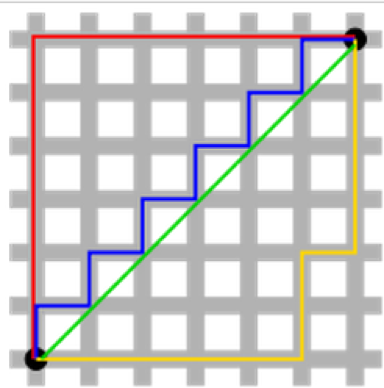
解决方案唯一性：这需要一点想象力。首先，看下图：

绿色的点（L2-norm）是唯一的最短路径。而红色，绿色，黄色（L1-norm）的线都是长度相同的路径。我们把它泛化到n维中，结果跟这里的二维一样。
内置的特征选择（Built-in feature
selection）：这是L1-norm经常被提及的一个优点，而L2-norm没有。这实际上是L1-norm的一个结果，L1-norm往往会使系数变得稀疏（sparse

coefficients）。假设模型有100个系数，但是有10个非零的系数，这就是说，其它90个预测器在预测目标值上是没有用的。L2-norm往往会有非稀疏的系数（non-sparse
coefficients），没有这个特点。
稀疏性（Sparsity）：这主要是一个向量或矩阵中只有很少的非零（non-zero）条目（entries）。L1-norm有能产生许多零值或非常小的值的系数的属性，很少有大的系数。
计算效率（Computational efficiency）：L1-norm没有一个解析解（analytical
solution），但是L2-nom有，这使得L2-norm可以被高效的计算。可是，L1-norm的解有稀疏的属性，它可以和稀疏算法一起用，这可以是计算更加高效。

参考文献

[1]. Differences between the L1-norm andthe L2-norm (Least Absolute Deviations and Least Squares).
http://www.chioka.in/differences-between-the-l1-norm-and-the-l2-norm-least-absolute-deviations-and-least-squares/

[2]. l0-Norm, l1-Norm, l2-Norm, … ,l-infinity Norm.

https://rorasa.wordpress.com/2012/05/13/l0-norm-l1-norm-l2-norm-l-infinity-norm/