11_数据降维PCA
1.sklearn降维API:sklearn. decomposition
2.PCA是什么:主成分分析
本质:PCA是一种分析、简化数据集的技术。
目的:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
作用:可以削减回归分析或者聚类分析中特征的数量。
当特征达到上百的时候,考虑是否要使用PCA来删除部分特征。
3.高维度数据容易出现的问题:特征之间通常是线性相关的。
4.PCA语法:
PCA(n_components=None) 将数据分解为较低维数空间
n_components:可以是小数,也可以是整数。为小数时,指定保存多少的数据量,通常是0.9~0.95,表示保存90%到95%的数据量。
为整数时,表示减少到多少特征数量,一般不使用整数。
PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features] 返回值:转换后指定维度的array
5.PCA演示过程:
1.初始化PCA,指定减少后的维度。
2.调用fit_transform
案例:
def pca():
"""
主成分分析进行特征降维
:return:
"""
pca = PCA(n_components=0.9)
data = pca.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
print(data) if __name__ == '__main__':
# normalization()
# stand()
# im()
# var()
pca()
结果:
[[ 1.28620952e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
6.简单的降维过程:
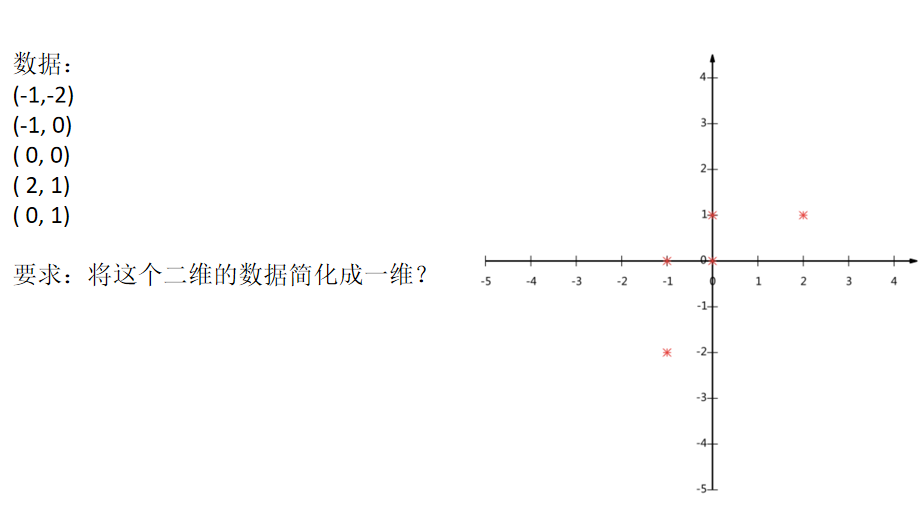
可以投向x轴和y轴,但是会丢失数据点,五个点变成三个点。
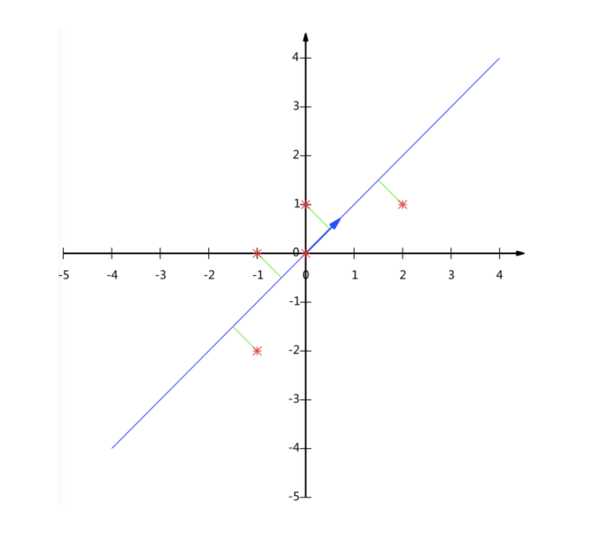

11_数据降维PCA的更多相关文章
- 数据降维-PCA主成分分析
1.什么是PCA? PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法.PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特 ...
- 数据降维PCA——学习笔记
PCA主成分分析 无监督学习 使方差(数据离散量)最大,更易于分类. 可以对隐私数据PCA,数据加密. 基变换 投影->内积 基变换 正交的基,两个向量垂直(内积为0,线性无关) 先将基化成各维 ...
- SIGAI机器学习第八集 数据降维1
讲授数据降维原理,PCA的核心思想,计算投影矩阵,投影算法的完整流程,非线性降维技术,流行学习的概念,局部线性嵌入,拉普拉斯特征映射,局部保持投影,等距映射,实际应用 大纲: 数据降维问题PCA的思想 ...
- [机器学习]-PCA数据降维:从代码到原理的深入解析
&*&:2017/6/16update,最近几天发现阅读这篇文章的朋友比较多,自己阅读发现,部分内容出现了问题,进行了更新. 一.什么是PCA:摘用一下百度百科的解释 PCA(Prin ...
- 主成分分析PCA数据降维原理及python应用(葡萄酒案例分析)
目录 主成分分析(PCA)——以葡萄酒数据集分类为例 1.认识PCA (1)简介 (2)方法步骤 2.提取主成分 3.主成分方差可视化 4.特征变换 5.数据分类结果 6.完整代码 总结: 1.认识P ...
- 降维PCA技术
降维技术使得数据变得更易使用,并且它们往往能够去除数据中的噪声,使得机器学习任务往往更加精确. 降维往往作为预处理步骤,在数据应用到其它算法之前清洗数据.有很多技术可以用于数据降维,在这些技术中,独立 ...
- Coursera《machine learning》--(14)数据降维
本笔记为Coursera在线课程<Machine Learning>中的数据降维章节的笔记. 十四.降维 (Dimensionality Reduction) 14.1 动机一:数据压缩 ...
- 数据降维技术(2)—奇异值分解(SVD)
上一篇文章讲了PCA的数据原理,明白了PCA主要的思想及使用PCA做数据降维的步骤,本文我们详细探讨下另一种数据降维技术—奇异值分解(SVD). 在介绍奇异值分解前,先谈谈这个比较奇怪的名字:奇异值分 ...
- 第七篇:数据预处理(四) - 数据归约(PCA/EFA为例)
前言 这部分也许是数据预处理最为关键的一个阶段. 如何对数据降维是一个很有挑战,很有深度的话题,很多理论书本均有详细深入的讲解分析. 本文仅介绍主成分分析法(PCA)和探索性因子分析法(EFA),并给 ...
随机推荐
- java编程——数据的加法
设计思想: 第一步:从键盘上输入一定个数的整数. 第二步:因为在main()方法中的参数是String类型的,所以第一步中输入的其实是字符类型,在这一步要把String转化成int. 第三步:初始化s ...
- override new 的区别
override : 方法提供从基类继承的成员的新实现. 通过 override 声明重写的方法称为重写基方法. 重写基方法必须具有与 override方法相同的签名 new : 关键字可以显式隐藏从 ...
- 【leetcode题目整理】数组中找子集
368. Largest Divisible Subset 题意:找到所有元素都不同的数组中满足以下规则的最大子集,规则为:子集中的任意两个元素a和b,满足a%b=0或者b%a=0. 解答:利用动态规 ...
- 数据库MySQL--子查询
例子文件1:https://files.cnblogs.com/files/Vera-y/myemployees.zip 子查询:又称内查询,出现在其他语句中的select语句 主查询:又称外查询,内 ...
- ios 中倒计时计算,时间戳为NaN
// 倒计时 daojishi(params) { let _this = this; let datetemp = this.servertimes; let lasttime = Date.par ...
- leetcode-212-单词搜索②
题目描述: 第一次提交:(超出时间限制) class Solution: def findWords(self, board: List[List[str]], words: List[str]) - ...
- thinkphp DEFINE标签
DEFINE标签用于中模板中定义常量,用法如下: 直线电机厂家 <define name="MY_DEFINE_NAME" value="3" /> ...
- c&c++MFC 调用 js 函数代码
调用函数代码和示例 Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlight ...
- AFO成功
在dcoi一年多,还是发生了不少事情. 过程中也有些小遗憾,有做错的事情,有搞砸的事情,有没办法挽回的事情,这种没法读档的辣鸡游戏也是无可奈何的.对所有被我搞砸的事情说声对不起啦,至少在下一次的时候, ...
- vue框架介绍
vue框架介绍 一.vue 概念 vue 是一种开发用户界面的渐进式开发框架.渐进式指的是:你可以将vue作为一部分嵌入到web应用中,带来丰富的交互体验 二.vue特点及常见开发中的高级功能 1.解 ...
