NOIP2009 codevs1173 洛谷P1073 最优贸易

Description：

国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城市的标号从 1~ n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

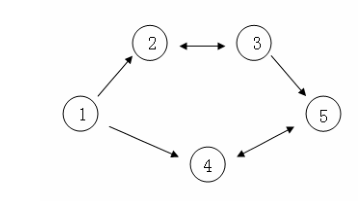
假设 1~n 号城市的水晶球价格分别为 4，3，5，6，1。

阿龙可以选择如下一条线路：1->2->3->5，并在 2 号城市以 3 的价格买入水晶球，在 3号城市以 5 的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路 1->4->5->4->5，并在第 1 次到达 5 号城市时以 1 的价格买入水晶球，在第 2 次到达 4 号城市时以 6 的价格卖出水晶球，赚取的旅费数为 5。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

Input：

第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 m 行，每行有 3 个正整数，x，y，z，每两个整数之间用一个空格隔开。如果 z=1，表示这条道路是城市 x 到城市 y 之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市y 之间的双向道路。

Output：

输出文件 trade.out 共 1 行，包含 1 个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 0。

思路：

书上和网上都是双向SPFA啊 因为NOIP并没有造数据卡SPFA…… 所以有些SPFA跑得很快 这里提供一种缩点+dp的做法

将贸易城市的强联通分量缩点，然后维护每个scc的最高价和最低价，然后对DAG进行一发DP就行了。

因为这是比较早的时候写得强联通，代码有点丑。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+,M = 1e6 + ;

int head[N],now;
struct edges{
    int to,next;
}edge[M<<];
void add(int u,int v){ edge[++now] = {v,head[u]}; head[u] = now;}

struct input{
    int x,y;
}inp[M];

int n,m,low[N],dfn[N],tot,cnt,pri[N],mx[N],mn[N],dict[N],ans;
bool exi[N];
stack<int> sta;
vector<int> vec[N];

void tarjan(int x){
    low[x] = dfn[x] = ++cnt; exi[x] = ;
    sta.push(x);
    for(int i = head[x];i ; i = edge[i].next){
        int v = edge[i].to;
        if(!dfn[v]){
            tarjan(v);  low[x] = min(low[x],low[v]);
        }
        else if(exi[v]) low[x] = min(low[x],dfn[v]);
    }
    if(dfn[x] == low[x]){
        tot++;
        while(x != sta.top()){
            int tmp = sta.top(); sta.pop();
            vec[tot].push_back(tmp);
            dict[tmp] = tot;
            exi[tmp] = ;
            mx[tot] = max(mx[tot],pri[tmp]);
            mn[tot] = min(mn[tot],pri[tmp]);
        }
        sta.pop();
        vec[tot].push_back(x);
        dict[x] = tot;
        exi[x] = ;
        mx[tot] = max(mx[tot],pri[x]);  mn[tot] = min(mn[tot],pri[x]);
    }
    return ;
}

int dp[N];
bool vis[N];
void dfs(int x){
    vis[x] = ;
    if(x == dict[n]) dp[x] = max(dp[x],mx[x]);
    for(int i = head[x]; i; i = edge[i].next){
        int v = edge[i].to;
        if(!vis[v])
          dfs(v);
        dp[x] = max(dp[x],dp[v]);
    }
    if(dp[x]) dp[x] = max(dp[x],mx[x]);
    ans = max(ans,dp[x] - mn[x]);
}

int main(){
    scanf("%d%d",&n,&m);
    int x,y,z;
    for(int i = ; i <= n; i++)
      scanf("%d",&pri[i]);
    memset(mx,-,sizeof(mx));  memset(mn,0x3f,sizeof(mn));
    for(int i = ; i <= m; i++){
        scanf("%d%d%d",&x,&y,&z);
        inp[i] = {x,y};
        add(x,y);
        if(z == ) add(y,x);
    }
    tarjan();
    memset(head,,sizeof(head));  now = ;
    memset(edge,,sizeof(edge));
    for(int i = ; i <= m; i++)
      if(dict[inp[i].x] != dict[inp[i].y])
        add(dict[inp[i].x],dict[inp[i].y]);
    dfs(dict[]);
    printf("%d\n",ans);
    return ;
}