HEER-Easing Embedding Learning by Comprehensive Transcription of Heterogeneous Information Networks

来源：KDD 2018

原文：HEER

code：https://github.com/GentleZhu/HEER

注： 若有错误，欢迎指正

 

这篇KDD’18的文章，没有按照常规的方法将所有的node嵌入到同一的空间，因为文章提出 node 因为连接的 edge 类型（type）不同，存在不兼容（incompatibility）的特性，所以最好能够根据不同的edge type来定义不同度量空间（metric space），保持同一个度量空间下，node的兼容性。

 

1. Abstract

在本文中，作者认为异构信息网络（HIN）中隐含着丰富信息的同时也引入了潜在的不兼容性，为了保留HIN中丰富但可能不兼容的信息，提出对HIN的综合转录问题。还需要提供一种易于使用的方法来有效利用 HIN 中的信息。本文提出HEER方法： 通过对 HIN 的边缘表示，与正确学习的异构度量相结合。

2. Introduction

网络嵌入学习节点的低维表示可以在原始网络中编码其语义信息，且容易和机器学习等方法相结合，可用于分类、链路预测。近来，研究人员证明了HIN 嵌入在作者识别等方面的有效性。

图 1 Network Embedding

 

HIN 异构性不仅包含丰富的信息，还有潜在的不兼容的语义。传统的同构网络嵌入不论其类型，均等的处理所有节点和边，不会捕捉 HIN 的异质性。

如图1，stan，musical，Ang Lee是不同类型的节点，因为musical和Ang Lee的embedding距离很远，会导致stan无法同时和两个embedding同时很近，因此需要学习两个不同的度量空间，从而stan分别在两个度量空间中与对应的node距离很近。

 

图 2 异质网络嵌入学习中的不兼容现象

 

为解决该问题，本文在计算相似度 s 时提出度量向量 μ

该度量向量μ是对不同类型的关系来进行embedding，g_{uv}是表示u,v之间的边的embedding。通过定义该相似度函数，能够获得基于不同边类型r的相似度

 

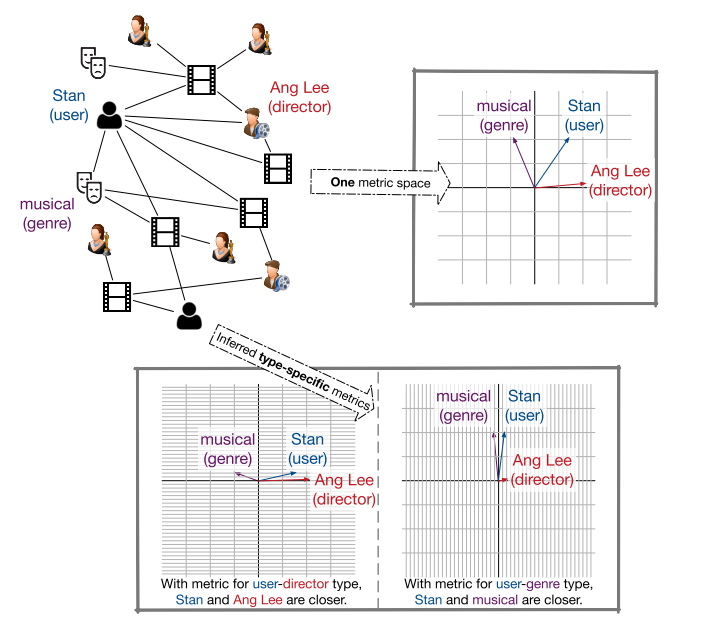
3. 嵌入 HINs 的边缘表示（HEER）

3.1. 方法思想

通过边缘表示和耦合度量的可用性，得到反应边的存在和类型的损失函数，通过最小化损失，同时更新节点嵌入、边缘嵌入和异构度量，保持输入HIN中的异质性。对不同的不兼容程度建模，其中两个边缘类型越相似，对应的指标越相似。

• 综合转录 HIN 中的嵌入信息
• 解决 HINs 中的语义不兼容
• 利用边缘表示和异质矩阵
• 使用神经网络学习节点和边的嵌入表示

3.2. 框架结构

图 3 HEER模型框架结构

 

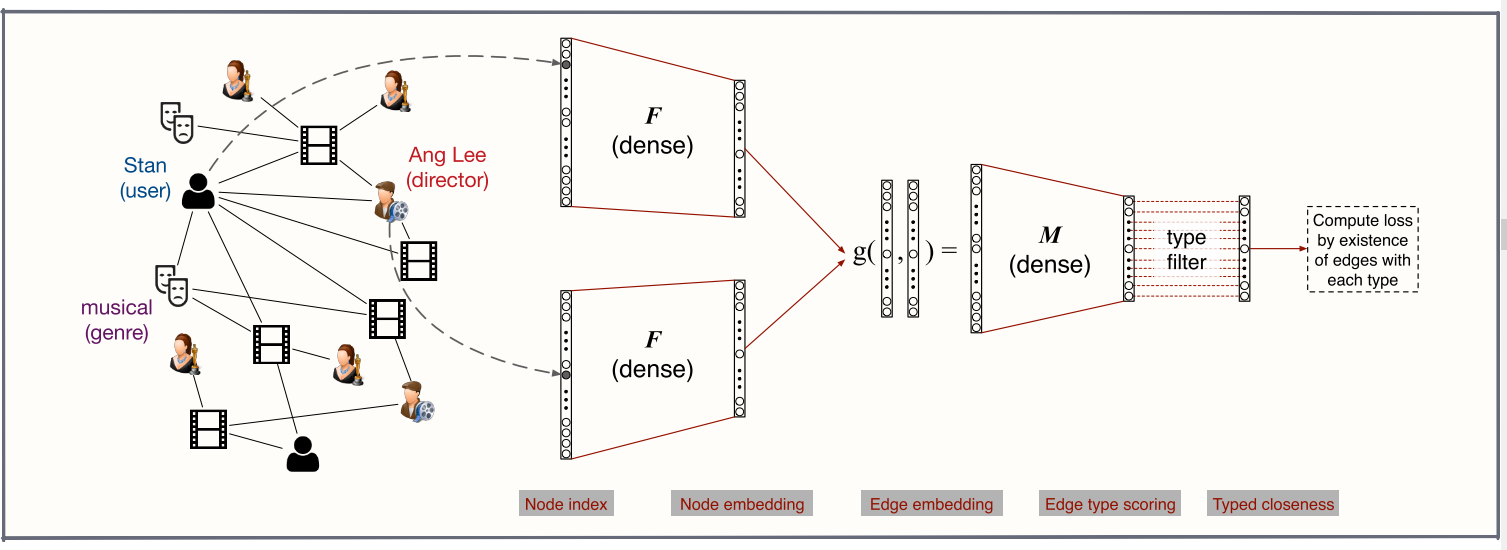
HIN Embedding 定义

• 输入一个异质网络

           

• 通过F网络学习出node embedding

           

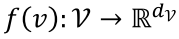
• 之后通过g函数来学习出边的embedding
• 一对节点间可能有多种类型的边，g(u,v) 包含此类关系

            

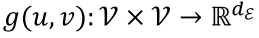
• 通过type之间的相似度，也就是定义的相似度函数和原始连接关系共同作为ground truth
• 最后训练出网络参数，从而能够学到网络的嵌入模型

类型接近度

对于每对节点（u，v）的边缘嵌入 guv

μr 为特定类型嵌入表示，兼容的边类型共享相似的 μ

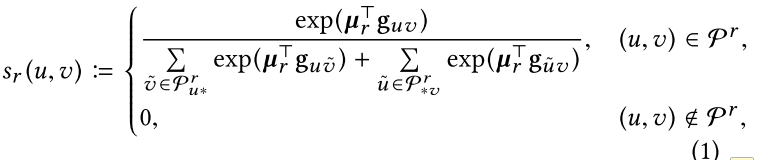
目标函数

（ KL 测量元权重和从嵌入表示得到的相似度间的差异）

将（1）代入（2）考虑所有的边类型，得到

 

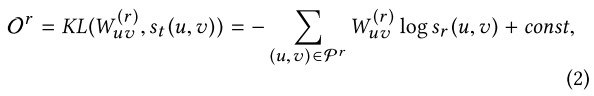
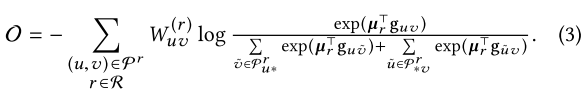
4. Experiment

 

 

 

（边缘剔除率为0.4时）

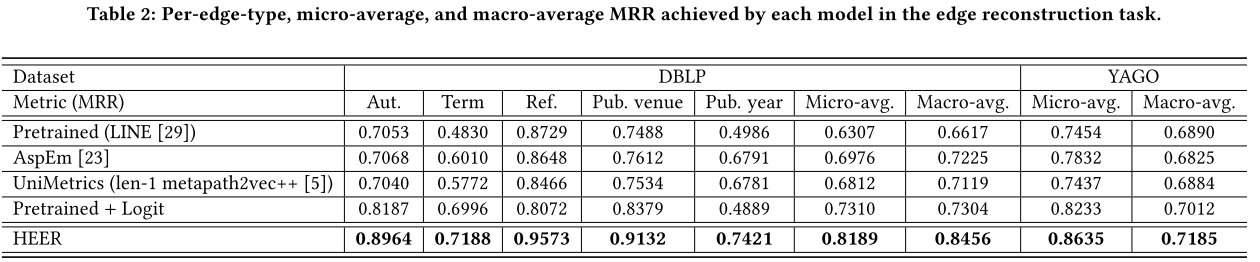
5. 总结

• HEER模型，能够建立异构网络中不同type之间的不兼容性，这是一种新的尝试，将不兼容的性质提出并通过不同度量空间来表示。
• HEER模型能够同时学习网络中节点的node embedding和边的edge embedding。

局限性

• 没有考虑更复杂的网络结构信息，而是仅仅通过相邻节点的关系来确定embedding，更复杂的关系可以通过meta-path来找到，这也可能成为该论文未来的研究方向。

参考：

KDD'18|异质信息网络嵌入学习