variable precision SWAR算法

计算二进制形式中1的数量这种问题，在各种刷题网站上比较常见，以往都是选择最笨的遍历方法“蒙混”过关。在了解Redis的过程中接触到了variable precision SWAR算法（以下简称VP-SWAR算法），算法异常简洁，是目前已知的同类方法中最快的。但如果对于位运算不是很熟悉的话，却不一定容易理解，所以有必要记录一下。

下面先看看VP-SWAR算法的完整实现，然后再逐行解释。

  public int vpSWAR(int i){
    i = (i & 0x55555555) + ((i>>1) & 0x55555555);
    i = (i & 0x33333333) + ((i>>2) & 0x33333333);
    i = (i & 0x0F0F0F0F) + ((i>>4) & 0x0F0F0F0F);
    i = (i * 0x01010101) >> 24;
    return i;
  }

VP-SWAR算法分为四步，第一步

i = (i & 0x55555555) + ((i>>1) & 0x55555555);

第一步的作用是计算每两位为一组的二进制形式包含1的个数。要理解这句话，我们需要从二进制的角度看看到底发生了什么。首先， 0x55555555 的二进制表示为 0101 0101 0101 0101 0101 0101 0101 0101 ，这个数字的规律是基数位为1，偶数位为0。为简单起见，我们只考虑两位，总共有四种情况，即：

i	x	i & x 结果
00	01	00
01	01	01
10	01	00
11	01	01

这里用x代表0b01(0b表示二进制)观察发现， i & (0b01) 是i的基数位对应x的1位，i的偶数位对应着x的0位， i & (0b01) 的结果会将i的偶数位置为0，而基数位保持不变，得到的结果就是i的基数位包含1的个数。 (i >> 1) & 0x55555555 先将i右移一位，也就是将i的基数位对应x的0位，i的偶数位对应着x的1位，然后再与 0x55555555 按位与，计算出来的是i的偶数位包含1的个数。两个计算结果相加就得到i每两位为一组中包含的1的数量，我们最后需要的就是这每两位一组的和。

第二步是在第一步的基础上，计算每四位为一组包含1的个数。按照每2位为一组分组用到了 0x55555555 这个数，那么自然的，按照每4位为一组分组自然就需要 0b0011 这种形式，这就是使用 0x33333333 的原因。理论上， i & (0b0011) 总共有16种情况，但是四位二进制位最多包含4个1，用二进制表示为 0b0100 ，所以经过第一步之后，i最多有5种取值，如下：

i	x	i & x 结果
0000	0011	0000
0001	0011	0001
0010	0011	0010
0011	0011	0011
0100	0011	0000

观察发现， i & (0b0011) 得到的是i的低两位包含1的个数，  (i >> 2) & 0b0011)得到的是i的高两位包含的1的个数，两个结果相加得到每四位包含的1的个数。注意，这里并不是说任何数与 0b0011 按位与得到的都是低两位包含的1的个数，这里的前提是第一步的计算，因为经过第一步计算之后，每两位包含多少个1已经记录了下来，再和 0b0011 按位与才得到正确的结果。例如， 0x0010 & 0x 0011=0x0010 ，但是我们不能说 0x0010 包含两个1，但是如果 0x0010 是经过第一步的计算得来，那才说明 0x0010 记录原始数据低两位有两个1。

第三步在第二步基础上，计算每8位有多少个1，由 0x01 和 0x0011 ，很自然想到 0x00001111 ，其对应的32位的十六进制数就是 0x0F0F0F0F 。

第四步就很有意思了，它不再是计算每16位包含1的个数，而是直接计算32位包含1的个数。对于32位的数来说，可以将其按每8位一组分为4组，分别用ABCD表示，例如 0x01020304 用这种形式表示为：

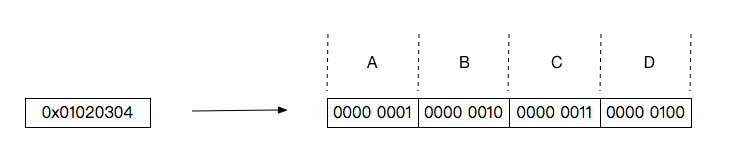
假设 0x01020304 是经过前三步计算之后得到的结果，那么要计算其总共包含多少个1，只需计算A+B+C+D。而ABCD表示的是不同的位区间范围，不能直接相加，该如何快速计算A+B+C+D的值呢？这里又用到了移位运算，将B、C、D分别左移8位、16位、24位，使其分别与A对齐：

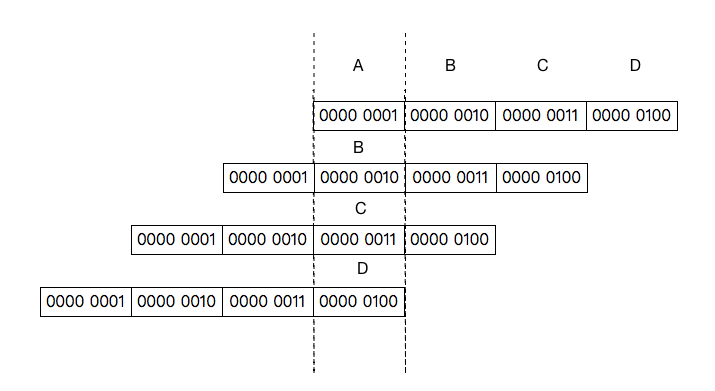
我们发现，将数字i分别左移0位、8位、16位、24位然后相加的结果，就是 i * 0x01010101 ，因为 i + (i << 8) + (i << 16) + (i << 24) = i * (1 + 1 << 8 + 1 << 16 + 1 << 24) = i * 0x01010101 。对于32位数字来说，左移之后超过32位的部分会被舍弃，低位补0，将左移之后得到的四个数字相加，结果的高8位的值就是原32位数包含的1的个数，要得到这个值，只需要将结果右移24位，将值放在低8位即可。

到这里，整个算法就结束了，右移的结果就是1的数量。在Redis中，BITCOUNT命令同时使用了查表法和VP-SWAR这两种方法。当要计算的位数小于128位时，使用查表法，否则使用VP-SWAR算法。其中查表法的做法是，程序先存一个256长度的表，按顺序记录从0-255（即 0b00000000 - 0b11111111） 数中二进制1的个数，然后对于输入参数每8位查一次表。