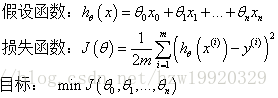岭回归与Lasso回归
线性回归的一般形式
过拟合问题及其解决方法
- 问题:以下面一张图片展示过拟合问题
- 解决方法:(1):丢弃一些对我们最终预测结果影响不大的特征,具体哪些特征需要丢弃可以通过PCA算法来实现;(2):使用正则化技术,保留所有特征,但是减少特征前面的参数θ的大小,具体就是修改线性回归中的损失函数形式即可,岭回归以及Lasso回归就是这么做的。
岭回归与Lasso回归
岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆这两类问题的,这两种回归均通过在损失函数中引入正则化项来达到目的,具体三者的损失函数对比见下图:
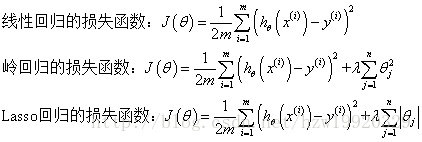
其中λ称为正则化参数,如果λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果λ选取过小,会导致对过拟合问题解决不当,因此λ的选取是一个技术活。
岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项,Lasso回归能够使得损失函数中的许多θ均变成0,这点要优于岭回归,因为岭回归是要所有的θ均存在的,这样计算量Lasso回归将远远小于岭回归。
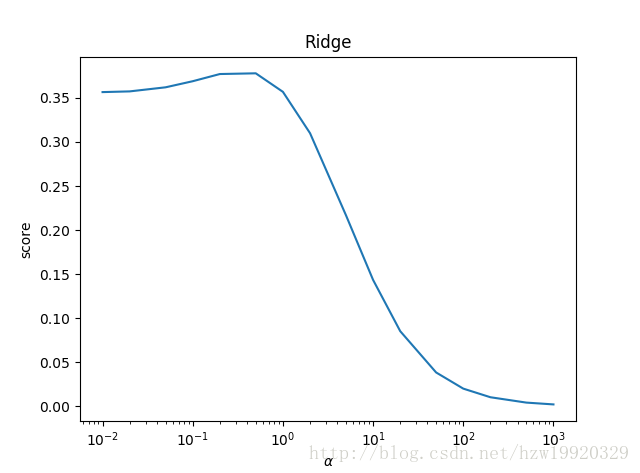
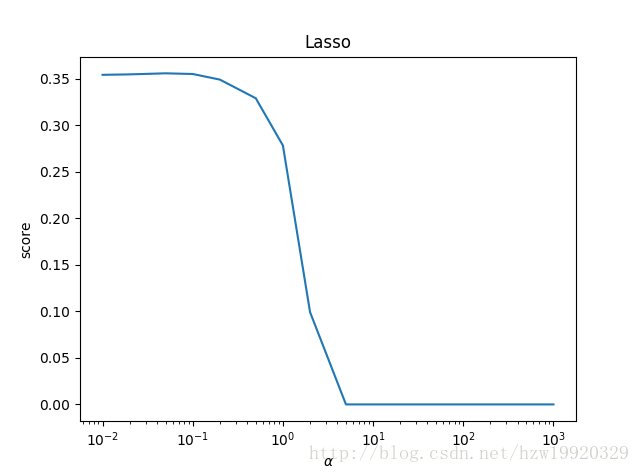
可以看到,Lasso回归最终会趋于一条直线,原因就在于好多θ值已经均为0,而岭回归却有一定平滑度,因为所有的θ值均存在。摘自:https://blog.csdn.net/hzw19920329/article/details/77200475
岭回归与Lasso回归的更多相关文章
- 多元线性回归模型的特征压缩:岭回归和Lasso回归
多元线性回归模型中,如果所有特征一起上,容易造成过拟合使测试数据误差方差过大:因此减少不必要的特征,简化模型是减小方差的一个重要步骤.除了直接对特征筛选,来也可以进行特征压缩,减少某些不重要的特征系数 ...
- 【机器学习】正则化的线性回归 —— 岭回归与Lasso回归
注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基本原理有一个透彻.直观的理解.直到最近再次接触到这个概念 ...
- 岭回归和Lasso回归以及norm1和norm2
norm代表的是距离,两个向量的距离:下图代表的就是p-norm,其实是对向量里面元素的一种运算: 最简单的距离计算(规范)是欧式距离(Euclidean distance),两点间距离是如下来算的, ...
- 岭回归和lasso回归(转)
回归和分类是机器学习算法所要解决的两个主要问题.分类大家都知道,模型的输出值是离散值,对应着相应的类别,通常的简单分类问题模型输出值是二值的,也就是二分类问题.但是回归就稍微复杂一些,回归模型的输出值 ...
- 机器学习之五 正则化的线性回归-岭回归与Lasso回归
机器学习之五 正则化的线性回归-岭回归与Lasso回归 注:正则化是用来防止过拟合的方法.在最开始学习机器学习的课程时,只是觉得这个方法就像某种魔法一样非常神奇的改变了模型的参数.但是一直也无法对其基 ...
- 线性回归大结局(岭(Ridge)、 Lasso回归原理、公式推导),你想要的这里都有
本文已参与「新人创作礼」活动,一起开启掘金创作之路. 线性模型简介 所谓线性模型就是通过数据的线性组合来拟合一个数据,比如对于一个数据 \(X\) \[X = (x_1, x_2, x_3, ..., ...
- 吴裕雄 数据挖掘与分析案例实战(7)——岭回归与LASSO回归模型
# 导入第三方模块import pandas as pdimport numpy as npimport matplotlib.pyplot as pltfrom sklearn import mod ...
- 机器学习入门线性回归 岭回归与Lasso回归(二)
一 线性回归(Linear Regression ) 1. 线性回归概述 回归的目的是预测数值型数据的目标值,最直接的方法就是根据输入写出一个求出目标值的计算公式,也就是所谓的回归方程,例如y = a ...
- 回归算法比较(线性回归,Ridge回归,Lasso回归)
代码: # -*- coding: utf-8 -*- """ Created on Mon Jul 16 09:08:09 2018 @author: zhen &qu ...
随机推荐
- websocket使用ssl 证书,开启加密服务
参考文章:https://fzambia.gitbooks.io/centrifugal/content/deploy/certificates.html TLS certificates TLS/S ...
- 设计模式之Protocol实现代理模式
使用场合 使用步骤 不使用protocol实现代理 使用protocol实现代理 一.使用场合 A想让B帮忙,就让B代理 A想通知B发生了一些事情,或者传一些数据给B 观察者模式 二.使用步骤 定义一 ...
- ubuntu下编译原生ffmpeg
本文主要介绍Linux 系统下如何编译Ffmpeg,编译环境是Ubuntu 16.04,Ffmpeg版本是3.4.2.Windows环境 下如何编译ffmpeg前面有博文介绍,也录有视频,感兴趣的同学 ...
- LVS-DR,real-server为windows 2008的配置
LVS-DR,real-server为windows 2008的配置 部署邮件系统负载均衡,采用LVS-DR模式,调度器是一台centos 5.8,real-server是两台windows2008, ...
- spring中的事件 applicationevent 讲的确实不错
event,listener是observer模式一种体现,在spring 3.0.5中,已经可以使用annotation实现event和eventListner里. 我们以spring-webflo ...
- Django之forms表单类
Form表单的功能 自动生成HTML表单元素 检查表单数据的合法性 如果验证错误,重新显示表单(数据不会重置) 数据类型转换(字符类型的数据转换成相应的Python类型) 1.创建Form类 from ...
- Spring Cloud Zuul API服务网关之请求路由
目录 一.Zuul 介绍 二.构建Spring Cloud Zuul网关 构建网关 请求路由 请求过滤 三.路由详解 一.Zuul 介绍 通过前几篇文章的介绍,我们了解了Spring Cloud ...
- 配置Spring的用于解决懒加载问题的过滤器
<?xml version="1.0" encoding="UTF-8"?><web-app version="2.5" ...
- Spring MVC学习纲要
感慨一下 之前用过Spring MVC, MyBatis,但是很久不用之后发现很多知识点都荒废了,毕竟工作就是重复,重复再重复.没有啥新东西.所以还是找个时间把忘了的东西捡起来.万一搞了个大bug,然 ...
- js时间戳格式化成日期格式的多种方法
js需要把时间戳转为为普通格式,一般的情况下可能用不到的, 下面先来看第一种吧 复制代码代码如下: function getLocalTime(nS) { return new Date(parseI ...