计蒜客NOIP模拟赛4 D2T1 鬼脚图

鬼脚图，又称画鬼脚，在日本称作阿弥陀签，是一种经典游戏，也是一种简易的决策方法，常常用来抽签或决定分配组合。

下图就是一张鬼脚图，其包含若干条竖线和若干条横线。请注意，横线只能水平连接相邻的两条竖线，且 在同一高度只会有一条横线。

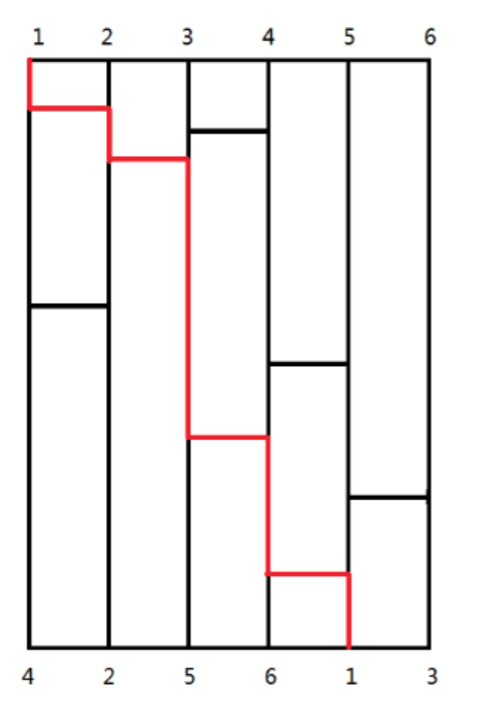
在图的上方，我们将这 n 条竖线依次标号为 1 到 n。以数字 3 为例，它会沿着所在的竖线下降，期间如果 遇到横线就会移动到横线的另一端，最终降落至下面的第一条竖线。上图中还标出了另外几种数字的最终位置。奇特的是，开始时每条竖线上都有一个数字，而 最终每条竖线下还是有一个数字。

现在，相信你一定已经理解了鬼脚图的规则，那么我们想请你完成下面的两个任务——

1. 读入一张有 n 条竖线和 m 条横线的鬼脚图，请你输出最下面一行的最终序列。

2. 如果让你设计一个鬼脚图最终序列达到上面的效果，你 最少需要多少条横线。

输入格式

第一行 2 个数字 n,m，表示竖线和横线的数量。

第二行 m 个数字，依次表示从高到低的横线。数字 a 的意义为，在第 a(1≤a<n)条竖线和第 a+1 条竖线间存在一条横线。

输出格式

第一行 n 个数字，表示该鬼脚图的最终序列。

第二行 1 个数字，表示最少需要多少条横线。

数据范围

对于 10% 的数据：n≤3,m≤5。

对于 20% 的数据：n≤4,m≤100。

对于 40% 的数据：n≤8,m≤1000。

对于 60%的数据：n≤1000,m≤5000。

对于 100%的数据：n≤100000,m≤1000000。

样例输入

3 3
1 2 1

样例输出

3 2 1
3
对于高度从大到小的横线,等价于在最终序列中交换
最终序列开始与初始序列相同
然后模拟,交换横线端点的值

第二问,要用最少步数得到
显然就是最终序列的逆序对数

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int n,m,a[],t[];
 long long ans;
 void partition(int l,int r)
 {
     if (l>=r)
         return;
     int mid=(l+r)/;
     partition(l,mid);
     partition(mid+,r);
     int i=l,j=mid+,k=l;
     while(i<=mid&&j<=r)
     {
         if(a[i]>a[j])
         {
             ans=(ans+mid-i+);
             t[k]=a[j];
             k++;
             j++;
         }
         else
         {
             t[k]=a[i];
             k++;
             i++;
         }
     }
     while(i<=mid)
     {
         t[k]=a[i];
         k++;
         i++;
     }
     while(j<=r)
     {
         t[k]=a[j];
         k++;
         j++;
     }
     for(i=l; i<=r; i++)
         a[i]=t[i];
 }
 int main()
 {int i,x;
     cin>>n>>m;
     for (i=;i<=n;i++)
     a[i]=i;
     for (i=;i<=m;i++)
     {
         scanf("%d",&x);
         swap(a[x],a[x+]);
     }
     for (i=;i<=n;i++)
         if (i<n)
         printf("%d ",a[i]);
  else cout<<a[i];
  partition(,n);
  cout<<endl<<ans;
 }