HDU 3944 DP? [Lucas定理 诡异的预处理]
DP?
Time Limit: 10000/3000 MS (Java/Others) Memory Limit: 128000/128000 K (Java/Others)
Total Submission(s): 3126 Accepted Submission(s): 978
数据范围诡异系列~
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=;
int n,m,P;
bool notp[N];
int p[N];
void sieve(int n){
for(int i=;i<=n;i++){
if(!notp[i]) p[++p[]]=i;
for(int j=;j<=p[]&&i*p[j]<=n;j++){
notp[i*p[j]]=;
if(i%p[j]==) break;
}
}
}
int fac[N][],mp[N],pnum;
void ini(int n){
sieve(n);
for(int j=;j<=p[];j++){
int x=p[j];mp[x]=j;
fac[][j]=;
for(int i=;i<=n;i++) fac[i][j]=fac[i-][j]*i%x;
}
}
int Pow(int a,int b){
int re=;
for(;b;b>>=,a=a*a%P)
if(b&) re=re*a%P;
return re;
}
int Inv(int a){return Pow(a,P-);}
int C(int n,int m){
if(n<m) return ;
return fac[n][pnum]*Inv(fac[m][pnum])%P*Inv(fac[n-m][pnum])%P;
}
int Lucas(int n,int m){
if(n<m) return ;
int re=;
for(;m;n/=P,m/=P) re=re*C(n%P,m%P)%P;
return re;
}
int main(){
freopen("in","r",stdin);
int cas=;
ini();
while(scanf("%d%d%d",&n,&m,&P)!=EOF){
if(m>n/) m=n-m;
pnum=mp[P];
printf("Case #%d: %d\n",++cas,(Lucas(n+,m)+n-m)%P);
}
}
HDU 3944 DP? [Lucas定理 诡异的预处理]的更多相关文章
- HDU 3944 DP? (Lucas定理)
题意:在杨辉三角中让你从最上面到 第 n 行,第 m 列所经过的元素之和最小,只能斜向下或者直向下走. 析:很容易知道,如果 m 在n的左半部分,那么就先从 (n, m)向左,再直着向上,如果是在右半 ...
- 【bzoj2111】[ZJOI2010]Perm 排列计数 dp+Lucas定理
题目描述 称一个1,2,...,N的排列P1,P2...,Pn是Mogic的,当且仅当2<=i<=N时,Pi>Pi/2. 计算1,2,...N的排列中有多少是Mogic的,答案可能很 ...
- hdu 3944 DP? 组合数取模(Lucas定理+预处理+帕斯卡公式优化)
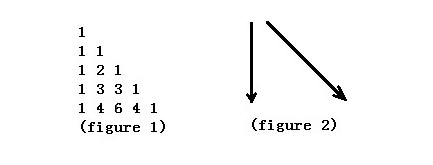
DP? Problem Description Figure 1 shows the Yang Hui Triangle. We number the row from top to bottom 0 ...
- BZOJ 2111 [ZJOI2010]Perm 排列计数:Tree dp + Lucas定理
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=2111 题意: 给定n,p,问你有多少个1到n的排列P,对于任意整数i∈[2,n]满足P[i ...
- [CTSC2017][bzoj4903] 吉夫特 [状压dp+Lucas定理]
题面 传送门 思路 一句话题意: 给出一个长度为 n 的序列,求所有长度大于等于2的子序列个数,满足:对于子序列中任意两个相邻的数 a和 b (b 在 a 前面),$C_a^b mod 2=1$,答案 ...
- bzoj 2111 [ZJOI2010]Perm 排列计数(DP+lucas定理)
[题目链接] http://www.lydsy.com/JudgeOnline/problem.php?id=2111 [题意] 给定n,问1..n的排列中有多少个可以构成小根堆. [思路] 设f[i ...
- hdu 3944 dp?
DP? Time Limit: 10000/3000 MS (Java/Others) Memory Limit: 128000/128000 K (Java/Others)Total Subm ...
- 【bzoj3782】上学路线 dp+容斥原理+Lucas定理+中国剩余定理
题目描述 小C所在的城市的道路构成了一个方形网格,它的西南角为(0,0),东北角为(N,M).小C家住在西南角,学校在东北角.现在有T个路口进行施工,小C不能通过这些路口.小C喜欢走最短的路径到达目的 ...
- 组合数(Lucas定理) + 快速幂 --- HDU 5226 Tom and matrix
Tom and matrix Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=5226 Mean: 题意很简单,略. analy ...
随机推荐
- CSS3动画属性和flex弹性布局各个属性
[CSS3动画的使用] 1.声明一个关键帧(动画): @keynames name{ from{} to{} } 每个阶段的写法: ①可以直接使用from-to的写法 ②可以设置0%-100%的写法, ...
- [国嵌攻略][059][2440-DMA程序设计]
初始化DMA控制器 1.设置源地址 DISRC(0x4B000000)设置为发送数据的源地址,DISRCC0(0x4B0000004)设置为内存AHB总线,目的地址增长 2.设置目的地址 DIDST0 ...
- SMTP错误码建议解决方法
https://wenku.baidu.com/view/0af30e01e87101f69e3195b8.html SMTP 错误码 / 建议解决方法 错误总表 101 Cannot Open Co ...
- 网站搭建中,怎么区分ASP和PHP
1:空间支持上 ASP:程序要求比较低,空间只要支持ASP+access即可运行 PHP:配置要求比较高,空间需要支持PHP及数据库,而且程序和数据库是单独的,一般的 unix空间都是这种配置. 2: ...
- -pie can only be used when targeting iOS 4.2 or later错误解决
在工程的build setting里,把IPHONEOS_DEPLOYMENT_TARGET改成4.2或以上就行了
- java LinkedLis t的26种使用方法
LinkedList类是双向列表,列表中的每个节点都包含了对前一个和后一个元素的引用. LinkedList的构造函数如下 1. public LinkedList(): --生成空的链表 2. p ...
- python_如何定义带参数的装饰器?
案例: 实现一个装饰器,用它来检查被装饰函数的参数类型. 需求: 装饰器可以通过函数,指明函数参数类型,进行函数调用的时候,传入参数,检测到不匹配时,抛出异常 如何解决这个问题? 先要获取函数的签名, ...
- linkin大话面向对象--组合
继承是实现类重用的重要手段,但是它有一个最大的坏处:破坏封装.相比之下,组合也是实现类重用的重要方式,但是采用组合方式实现类重用则能提供更好的封装性.比如人有手一样,在人的类中增加一个手的属性. 何时 ...
- svn: resource out of date; try updating的解决
问题: svn提交文件时提示错误:resource out of date; try updating.说明该资源版本有问题,尝试更新svn,发现该文件没有可更新的内容.于是查看资源历史,发现有人第一 ...
- Part 1:请求与响应--Django从入门到精通系列教程
该系列教程系个人原创,并完整发布在个人官网刘江的博客和教程 所有转载本文者,需在顶部显著位置注明原作者及www.liujiangblog.com官网地址. Python及Django学习QQ群:453 ...
