原创作品出处原始出处、作者信息和本声明。否则将追究法律责任。http://sbp810050504.blog.51cto.com/2799422/1608064

Logistic回归与梯度上升算法

在《机器学习实战》一书的第5章中讲到了Logistic用于二分类问题。书中只是给出梯度上升算法代码，但是并没有给出数学推导。故哪怕是简单的几行代码，依然难以理解。

对于Logistic回归模型而言，需要读者具有高等数学、线性代数、概率论和数理统计的基础的数学基础。高等数学部分能理解偏导数即可；线性代数部分能理解矩阵乘法及矩阵转置即可；概率论和数理统计能理解条件概率及极大似然估计即可。

有《高等代数》(浙大)、概率论与数理统计(浙大)、线性代数(同济大学)三本数学足矣。

Logistic回归用于二分类问题，面对具体的二分类问题，比如明天是否会下雨。人们通常是估计，并没有十足的把握。因此用概率来表示再适合不过了。

Logistic本质上是一个基于条件概率的判别模型(DiscriminativeModel)。利用了Sigma函数值域在[0,1]这个特性。

函数图像为：

通过sigma函数计算出最终结果，以0.5为分界线，最终结果大于0.5则属于正类(类别值为1)，反之属于负类(类别值为0)。

如果将上面的函数扩展到多维空间，并且加上参数，则函数变成：

其中X是变量，θ是参数，由于是多维，所以写成了向量的形式，也可以看作矩阵。θ^T表示矩阵θ的转置，即行向量变成列向量。θ^TX是矩阵乘法。（高数结合线性代数的知识）

如果我们有合适的参数向量θ，以及样本x，那么对样本x分类就可以通过上式计算出一个概率值来，如果概率值大于0.5，我们就说样本是正类，否则样本是负类。

比如，对于“垃圾邮件判别问题”，对于给定的邮件(样本)，我们定义非垃圾邮件为正类，垃圾邮件为负类。我们通过计算出的概率值即可判定邮件是否是垃圾邮件。

接下来问题来了，如何得到合适的参数向量θ呢？

由于sigma函数的特性，我们可作出如下的假设：

上式即为在已知样本X和参数θ的情况下，样本X属性正类(y=1)和负类(y=0)的条件概率。

将两个公式合并成一个，如下：

既然概率出来了，那么最大似然估计也该出场了。假定样本与样本之间相互独立，那么整个样本集生成的概率即为所有样本生成概率的乘积：

其中，m为样本的总数，y⁽ⁱ⁾表示第i个样本的类别，x⁽ⁱ⁾表示第i个样本，需要注意的是θ是多维向量，x⁽ⁱ⁾也是多维向量。

（接下来从《概率论与数理统计》转到《高等数学》）

为了简化问题，我们对整个表达式求对数，(将指数问题对数化是处理数学问题常见的方法)：

上式是基本的对数变换，高中数学而已，没有复杂的东西。

满足似然函数(θ)的最大的θ值即是我们需要求解的模型。

梯度上升算法

如此复杂的函数，如何求满足函数(θ)最大值的参数向量θ呢？

如果问题简化到一维，就很好办了。假如需要求取函数：

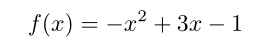
的最大值。

函数图像如下：

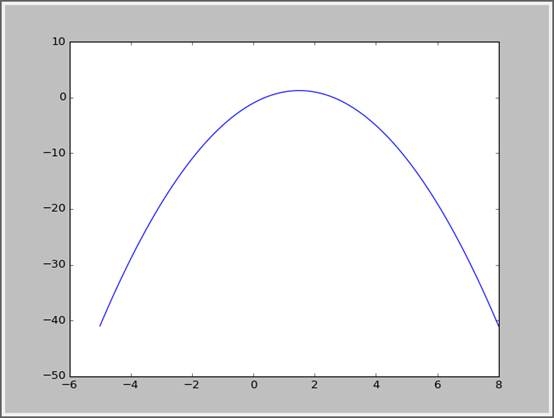
函数的导数为：

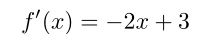
所以 x=1.5即取得函数的最大值1.25

但是真实环境中的函数不会像上面这么简单，就算求出了函数的导数，也很难精确计算出函数的极值。此时我们就可以用迭代的方法来做。就像爬坡一样，一点一点逼近极值。爬坡这个动作用数学公式表达即为：

其中，α为步长。

求上面函数极值的Python代码如下：

def f_prime(x_old):

return -2*x_old+3

def cal():

x_old=0

x_new=6

eps=0.01

presision=0.00001

whileabs(x_new-x_old)>presision:

x_old=x_new

x_new=x_old+eps*f_prime(x_old)

return x_new

结果为：1.50048

回到Logistic Regression问题，我们同样对函数求偏导。

这个公式有点复杂，但是依然只是基本的导数变换，待我细细拆解。这里需要的数学知识无外乎两点：函数的和、差、积、商求导法则和复合函数的求导法则(高等数学P88页)。

先看：

其中：

再由：

可得：

接下来就剩下第三部分：

(这个公式应该很容易理解，简单的偏导公式)

还有就是：

综合三部分即得到：

因此，梯度迭代公式为：

结合本式再去理解《机器学习实战》中的代码就很简单了。

参考http://cs229.stanford.edu/notes/cs229-notes1.pdf

文档中的公式是用LaTex弄出来的，比word中好看多了。

如果有什么问题，可加微博 @帅广应s

Me是数学渣啊~