编程之美Q1

题目

和数书页有点类似，就直接数吧

#include<iostream>
using namespace std;
class q1
{
	public:
		size_t func(size_t num);
};
size_t q1::func(size_t num)
{
	size_t count = 0, tmp;
	while(num)
	{
		tmp = num;
		while(tmp)
		{
			if(tmp%10 == 1)
				++count;
			tmp = tmp/10;
		}
		--num;
	}
	return count;
}

int main()
{
	q1 an;
	size_t num = 0;
	while(1)
	{
	cout<<"please input positive integer: ";
	cin>>num;
	cout<<num<<" to 0 include "<<an.func(num)<<" number 1 ."<<endl;
	}
	//num = 0xffffffff;
	//cout<<num<<" to 0 include "<<an.func(num)<<" number 1 ."<<endl;
}

可循环输入，运行效果

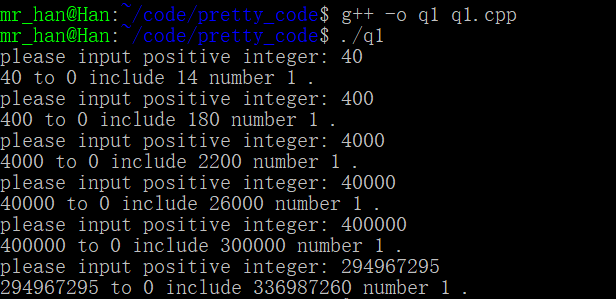
显然，时间复杂度过高，一定有其他方法

先看 1 位数的情况。

如果 N = 3，那么从 1 到 3 的所有数字：1、2、3，只有个位数字上可能出现 1，而且只出现 1 次，进一步可以发现如果 N 是个位数，如果 N>=1，那么 f（N）都等于 1，如果 N=0，则 f（N为 0。

再看 2 位数的情况。

如果 N=13，那么从 1 到 13 的所有数字：1、2、3、4、5、6、7、8、9、10、11、12、13，个位和十位的数字上都可能有 1，我们可以将它们分开来考虑，个位出现 1 的次数有两次：1 和 11，十位出现 1 的次数有 4 次：10、11、12 和 13，所以 f（N）=2+4=6。要注意的是 11 这个数字在十位和个位都出现了 1，但是 11 恰好在个位为 1 和十位为 1 中被计算了两次，所以不用特殊处理，是对

的。再考虑 N=23 的情况，它和 N=13 有点不同，十位出现 1 的次数为 10 次，从 10 到 19，个位出现 1 的次数为 1、11 和 21，所以f（N）=3+10=13。通过对两位数进行分析，我们发现，个位数出现 1 的次数不仅和个位数字有关，还和十位数有关：如果 N 的个位数大于等于 1，则个位出现 1 的次数为十位数的数字加 1；如果N 的个位数为 0，则个位出现 1 的次数等于十位数的数字。而十位数上出现 1 的次数不仅和十位数有关，还和个位数有关：如果十位数字等于 1，则十位数上出现 1 的次数为个位数的数字加 1；如果十位数大于 1，则十位数上出现 1 的次数为 10。

 

接着分析 3 位数

如果 N = 123：

个位出现 1 的个数为 13：1, 11, 21, …, 91, 101, 111, 121

十位出现 1 的个数为 20：10～19, 110～119

百位出现 1 的个数为 24：100～123

f（23）= 个位出现 1 的个数 + 十位出现 1 的个数 + 百位出现 1 的次数 = 13 + 20 + 24 = 57；

根据上面的一些尝试，下面我们推导出一般情况下，从 N 得到 f（N）的计算方法：

假设 N=abcde，这里 a、b、c、d、e 分别是十进制数 N 的各个数位上的数字。如果要计算百位上出现 1 的次数，它将会受到三个因素的影响：百位上的数字，百位以下（低位）的数字，百位（更高位）以上的数字。

如果百位上的数字为 0，则可以知道，百位上可能出现 1 的次数由更高位决定，比如 12 013，则可以知道百位出现 1 的情况可能是 100～199，1 100～1 199，2 100～2 199，…，11 100~11 199，一共有 1 200 个。也就是由更高位数字（12）决定，并且等于更高位数字（12）×当前位数（100）。

如果百位上的数字为 1，则可以知道，百位上可能出现 1 的次数不仅受更高位影响，还受低位影响，也就是由更高位和低位共同决定。例如对于 12 113，受更高位影响，百位出现 1 的情况是 100～

199，1 100～1 199，2 100～2 199，…，11 100~11 199，一共 1 200个，和上面第一种情况一样，等于更高位数字（12）×当前位数（100）。但是它还受低位影响，百位出现 1 的情况是 12100～12 113，一共14 个，等于低位数字（13）+1。

如果百位上数字大于 1（即为 2~9），则百位上可能出现 1的次数也仅由更高位决定，比如 12 213，则百位出现 1 的可能性为：100～199，1 100～1 199，2 100～2 199，…，11 100～11 199，12 100～12 199，一共有 1 300 个，并且等于更高位数字+1（12+1）×当前位数（100）。

所以利用这个规律我们可以写出新的更高效的算法

#include<iostream>
using namespace std;
class q1
{
	public:
		size_t func(size_t num);
		size_t func1(size_t num);
		size_t equ(size_t befor, size_t num);
};
size_t q1::func(size_t num)
{
	size_t count = 0, tmp;
	while(num)
	{
		tmp = num;
		while(tmp)
		{
			if(tmp%10 == 1)
				++count;
			tmp = tmp/10;
		}
		--num;
	}
	return count;
}

size_t q1::func1(size_t num)
{
	size_t Ncount = 0;
	size_t Nlower = 0;
	size_t Ncurrent = 0;
	size_t Nhigher = 0;
	size_t circle = 1;
	while(num/circle != 0)
	{
		Nlower = num - (num/circle)*circle;
		Ncurrent = (num/circle)%10;
		Nhigher = num/(circle*10);

		switch(Ncurrent)
		{
			case 0:
				Ncount += Nhigher*circle;//当前位是0
				break;
			case 1:
				Ncount += Nhigher*circle + Nlower;//当前位是1
				break;
			default:
				Ncount += (Nhigher+1)*circle;//当前位置不是0或1
				break;

		}
		circle *= 10;
	}
	return Ncount;
}

int main()
{
	q1 an;
	size_t num;
	while(1)
	{
		cout<<"please input positive integer: ";
		cin>>num;
		cout<<num<<" to 0 include "<<an.func1(num)<<" number 1 ."<<endl;
	}
}

运行一下，发现即使数字很大相当快，编程之美作者牛逼

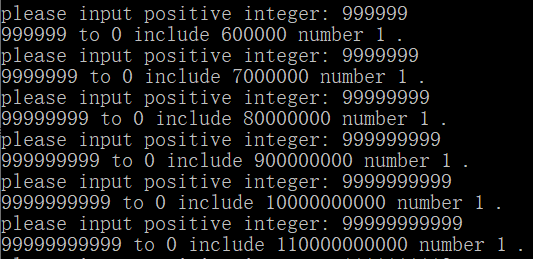
第二问，作者的答案是

然而，将n = 1 111 111 110输入

虽然很接近，但是最大N确实不在此点，而且经过手动校验，也不在这附近。

使用图像法，只要找出y = func1(N)和y = x两个函数交点即可。 由实践可知交点不止一个，并且有交点非整数。

进行遍历对比，效率很低，发现了存在这么多 N = func(N)

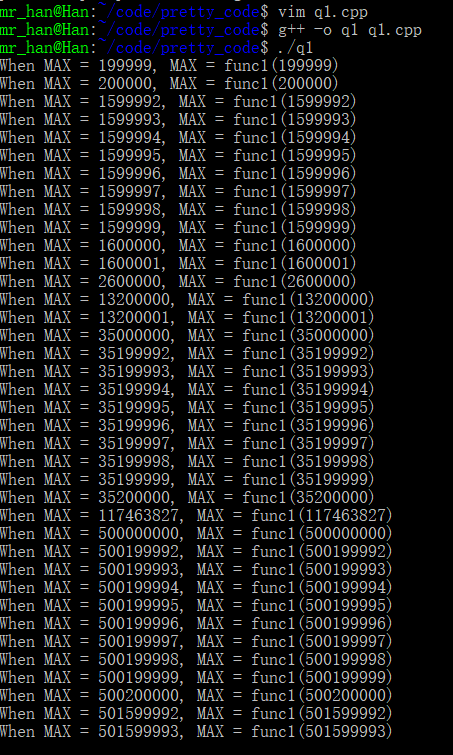
程序跑到这里，已经被操作系统强行终止了，但是我们知道在1~2^32 - 1 这个区间范围内应该还有更大的数字满足N = func1(N)，现在遍历已经行不通了，所以建议使用MATLAB将 y=x 和 y = func1(x)这两个曲线绘出来，然后在估算交点区间，在小区间内进行更高效的遍历，这样可以快速找出答案。