机器学习(七) PCA与梯度上升法 (下)

五、高维数据映射为低维数据

换一个坐标轴。在新的坐标轴里面表示原来高维的数据。

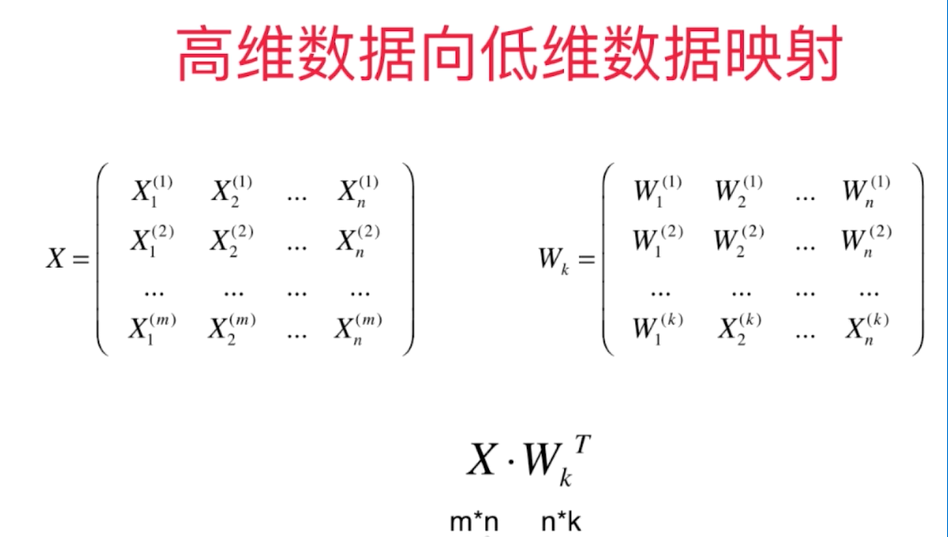
低维 反向 映射为高维数据

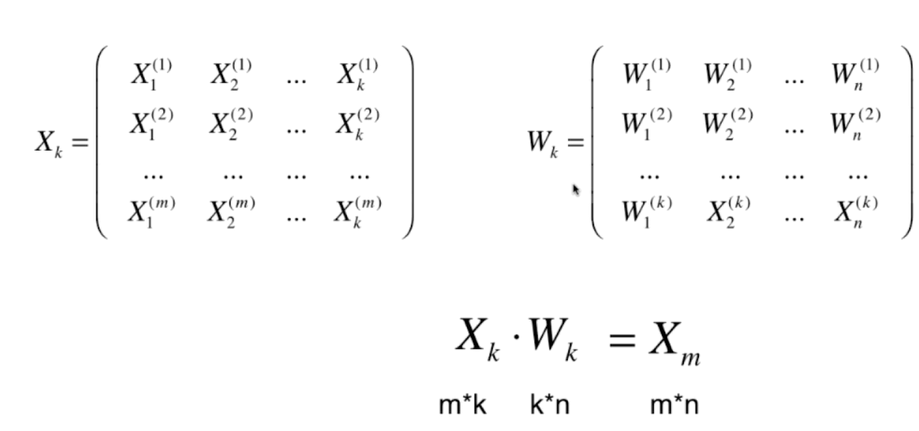
PCA.py

import numpy as np

class PCA:

    def __init__(self, n_components):
        """初始化PCA"""
        assert n_components >= 1, "n_components must be valid"
        self.n_components = n_components
        self.components_ = None

    def fit(self, X, eta=0.01, n_iters=1e4):
        """获得数据集X的前n个主成分"""
        assert self.n_components <= X.shape[1], \
            "n_components must not be greater than the feature number of X"

        def demean(X):
            return X - np.mean(X, axis=0)

        def f(w, X):
            return np.sum((X.dot(w) ** 2)) / len(X)

        def df(w, X):
            return X.T.dot(X.dot(w)) * 2. / len(X)

        def direction(w):
            return w / np.linalg.norm(w)

        def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8):

            w = direction(initial_w)
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = df(w, X)
                last_w = w
                w = w + eta * gradient
                w = direction(w)
                if (abs(f(w, X) - f(last_w, X)) < epsilon):
                    break

                cur_iter += 1

            return w

        X_pca = demean(X)
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
        for i in range(self.n_components):
            initial_w = np.random.random(X_pca.shape[1])
            w = first_component(X_pca, initial_w, eta, n_iters)
            self.components_[i,:] = w

            X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w

        return self

    def transform(self, X):
        """将给定的X，映射到各个主成分分量中"""
        assert X.shape[1] == self.components_.shape[1]

        return X.dot(self.components_.T)

    def inverse_transform(self, X):
        """将给定的X，反向映射回原来的特征空间"""
        assert X.shape[1] == self.components_.shape[0]

        return X.dot(self.components_)

    def __repr__(self):
        return "PCA(n_components=%d)" % self.n_components

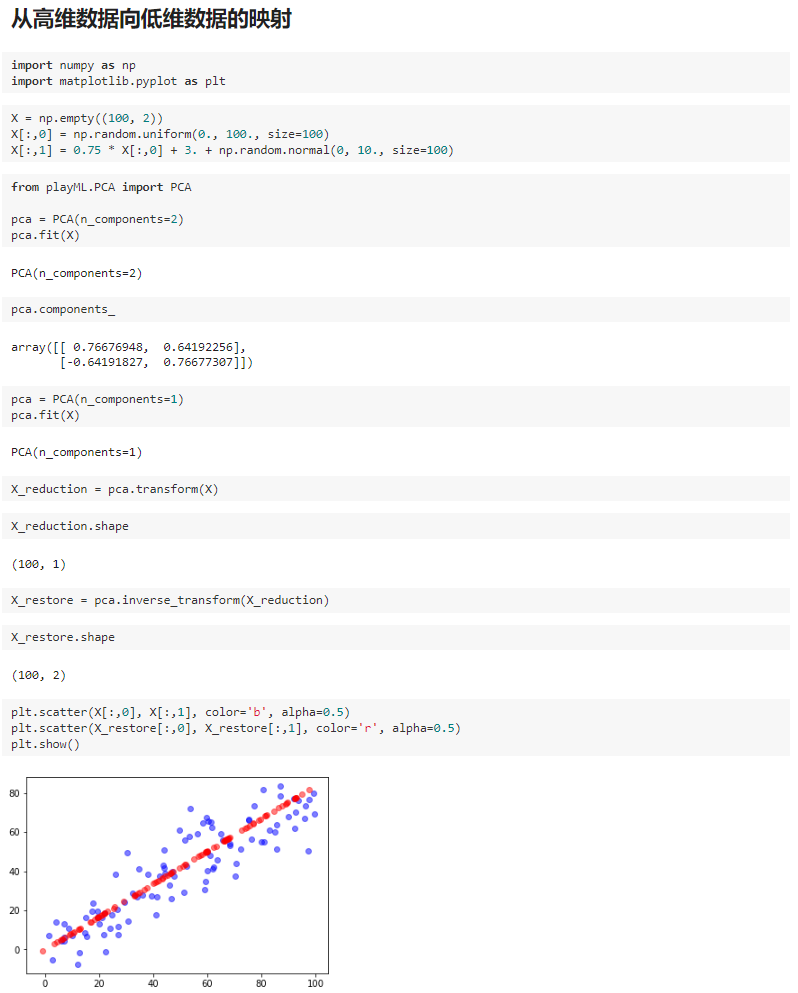
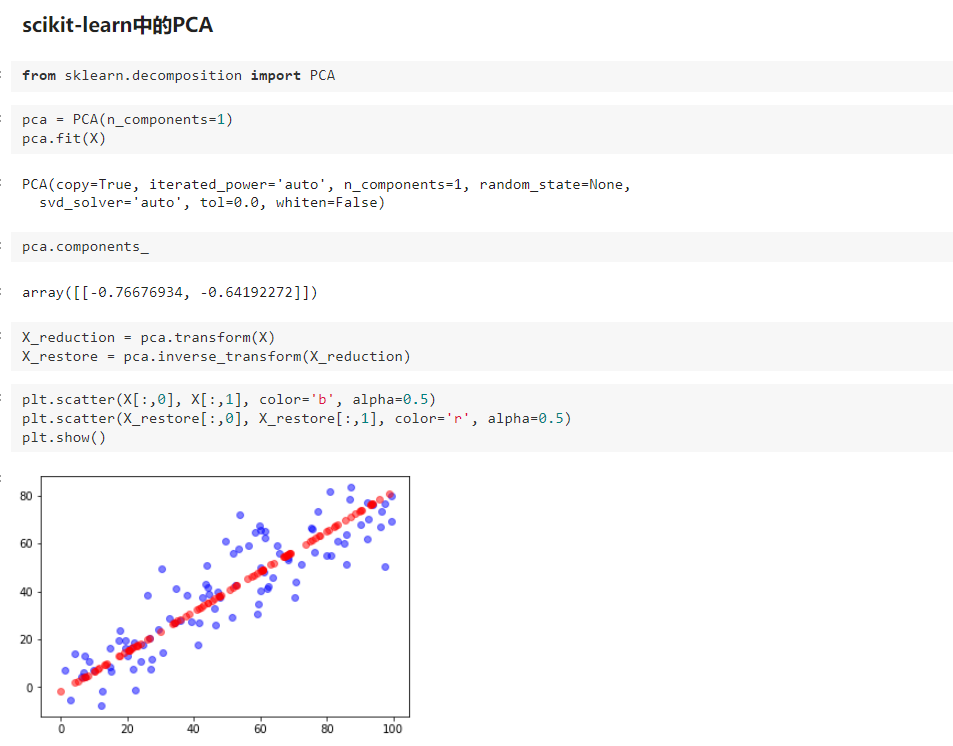
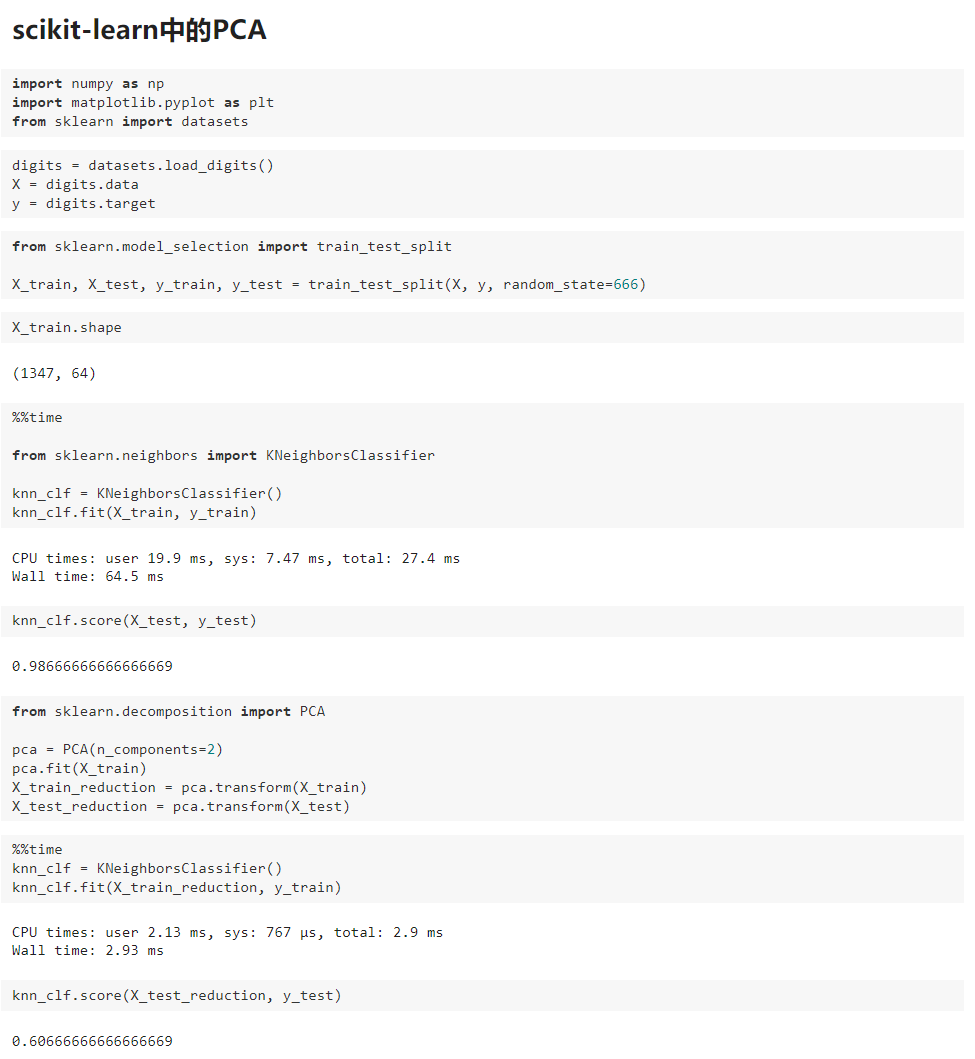
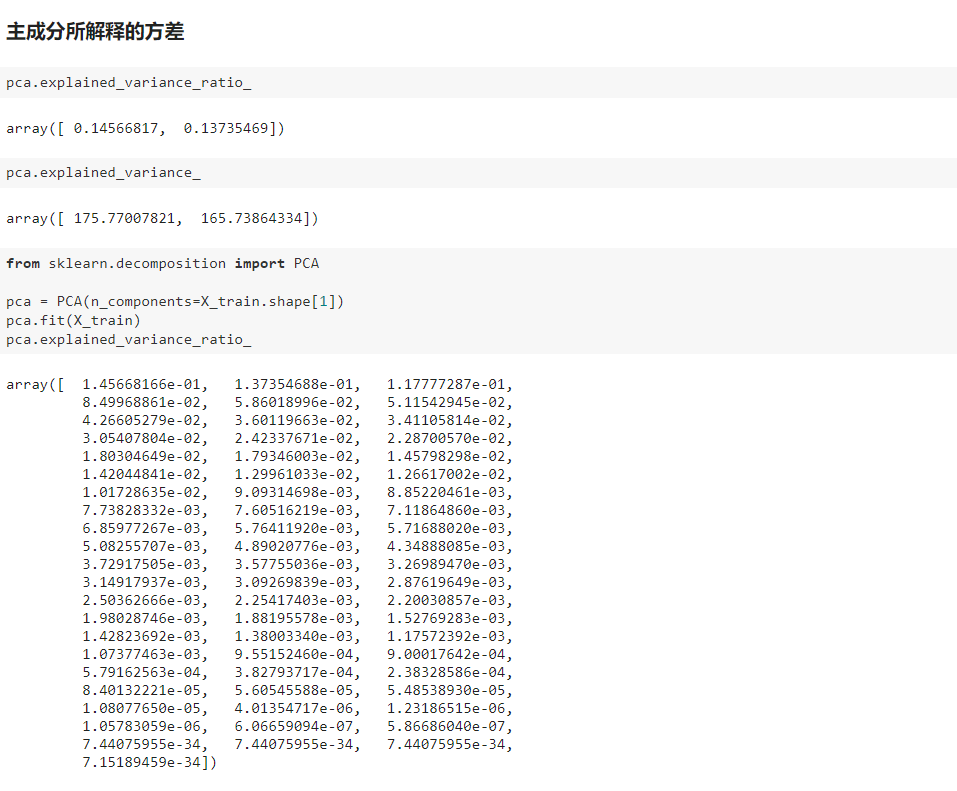
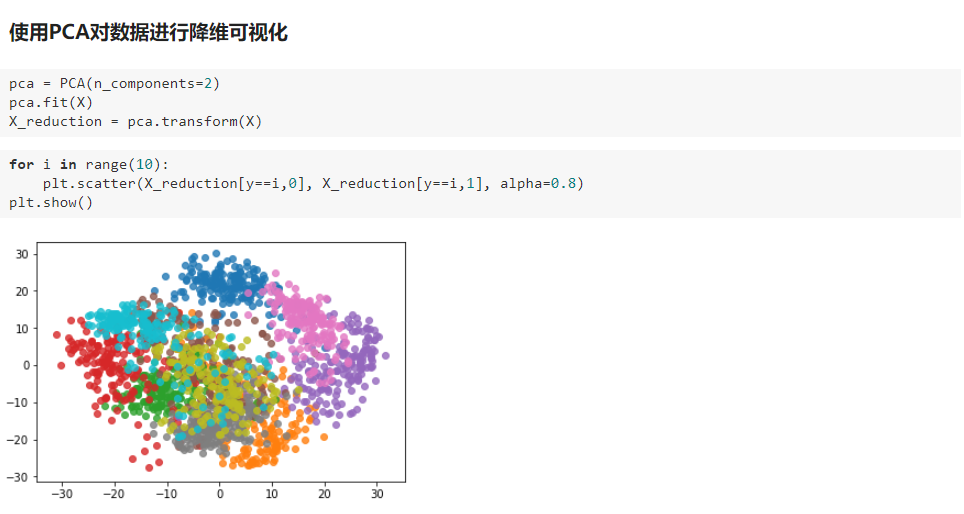
六、scikit-learn 中的 PCA

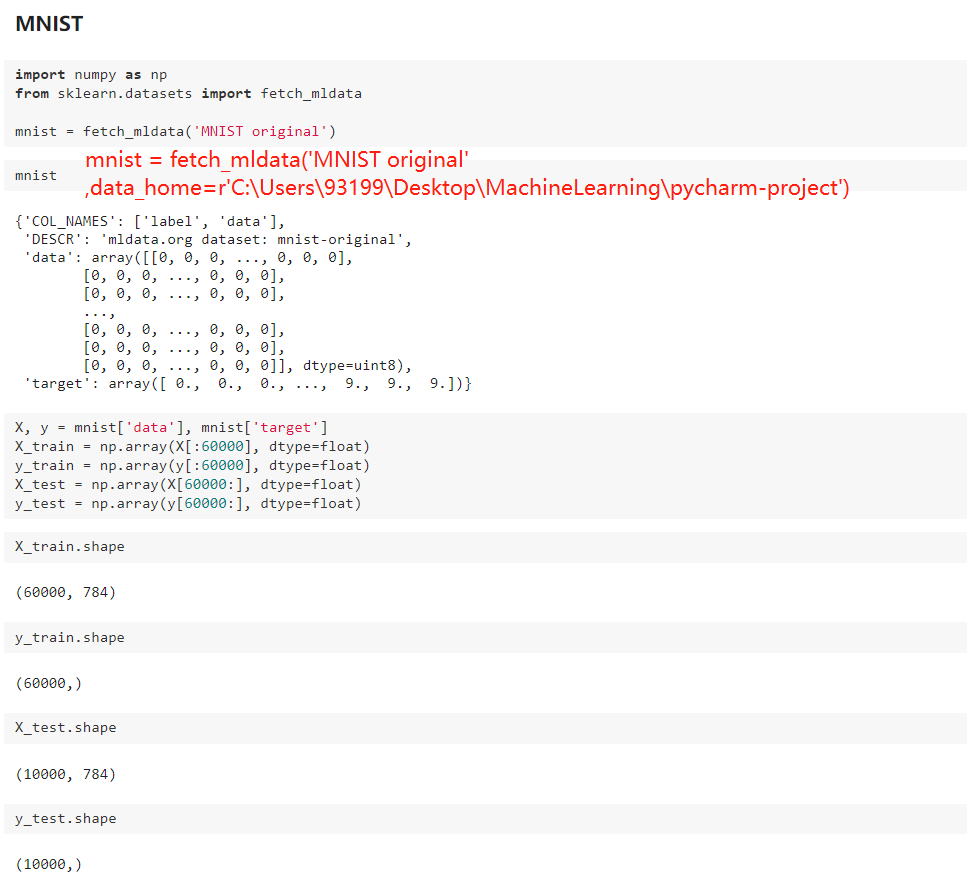
七、试手MNIST数据集

通过单幅图像数据的高维化,将单幅图像转化为高维空间中的数据集合,对其进行非线性降维,寻求其高维数据流形本征结构的一维表示向量,将其作为图像数据的特征表达向量。从而将高维图像识别问题转化为特征表达向量的识别问题,大大降低了计算的复杂程度,减少了冗余信息所造成的识别误差,提高了识别的精度。通过指纹图像的实例说明,将非线性降维方法(如Laplacian Eigenmap方法)应用于图像数据识别问题,在实际中是可行的,在计算上是简单的,可大大改善常用方法(如K-近邻方法)的效能,获得更好的识别效果。此外,该方法对于图像数据是否配准是不敏感的,可对不同大小的图像进行识别,这大大简化了识别的过程

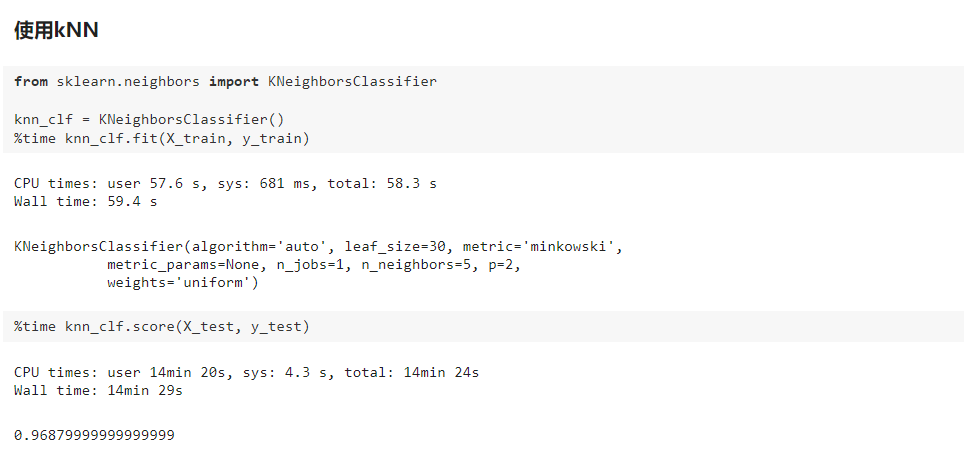
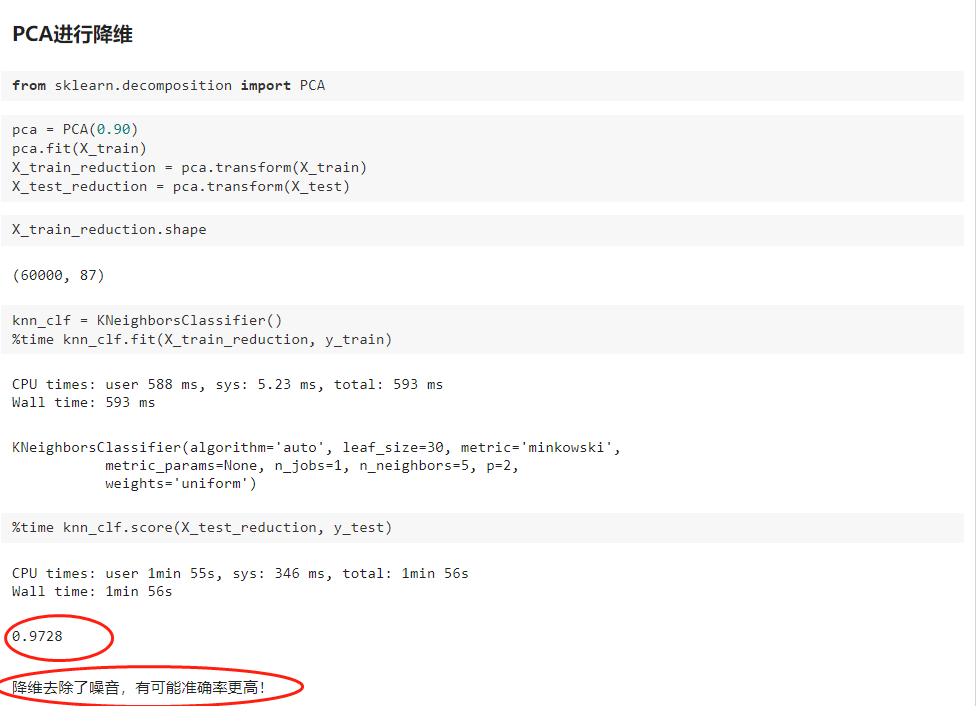
八、使用PCA对数据进行降噪

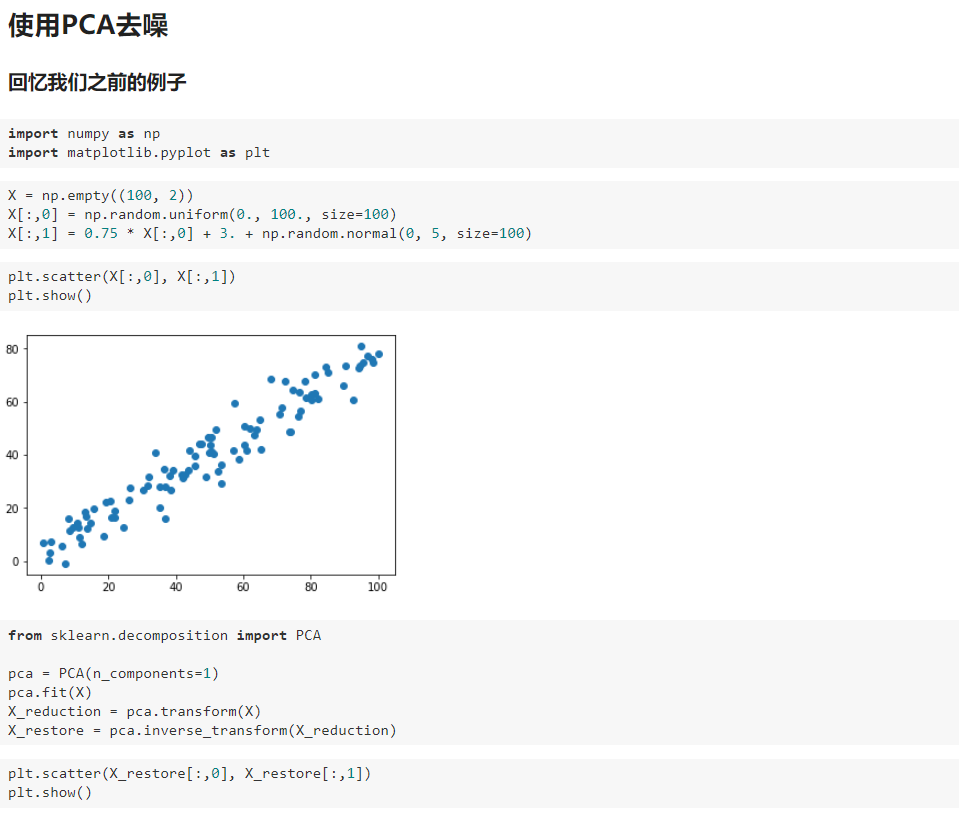
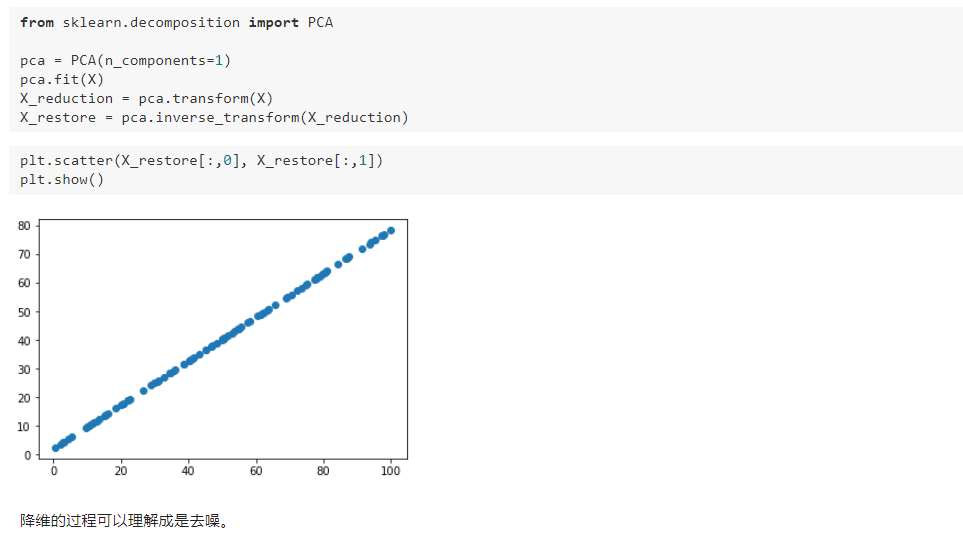
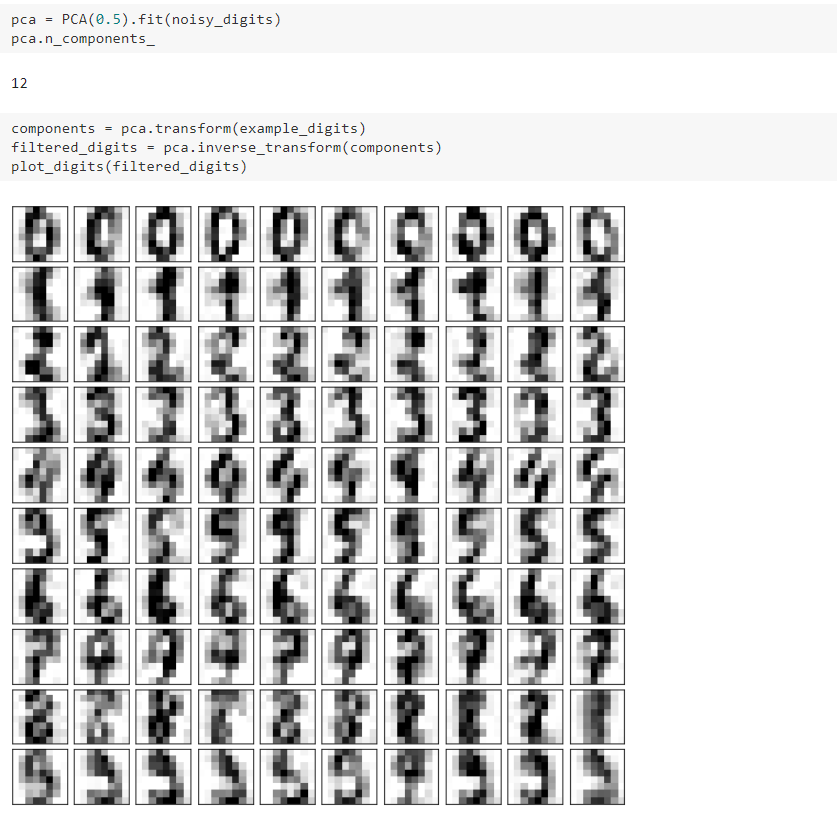
九、人脸识别与特征脸

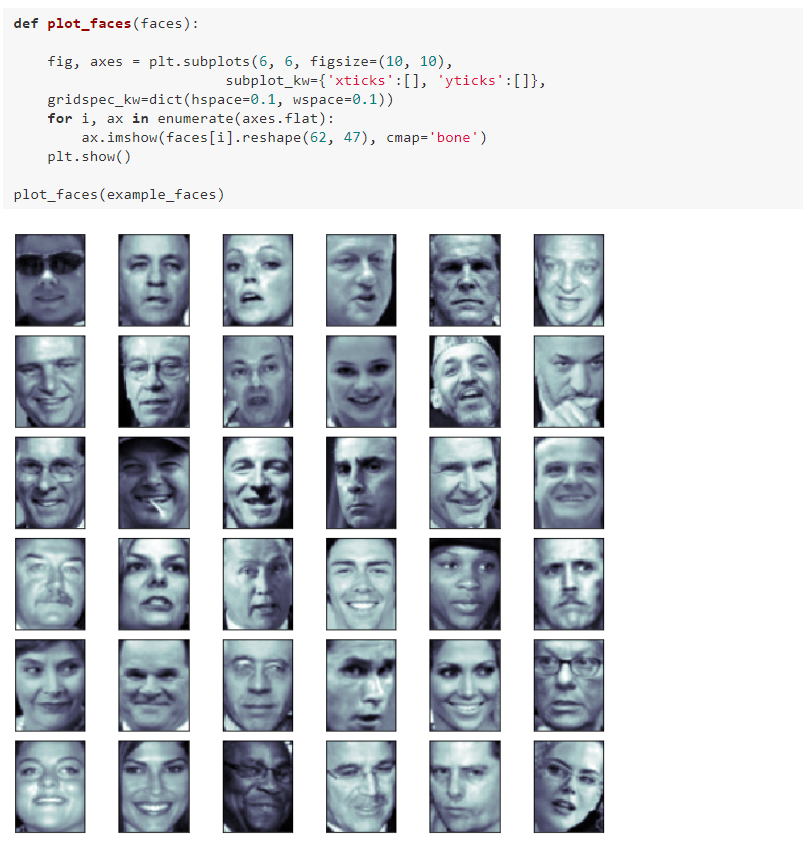
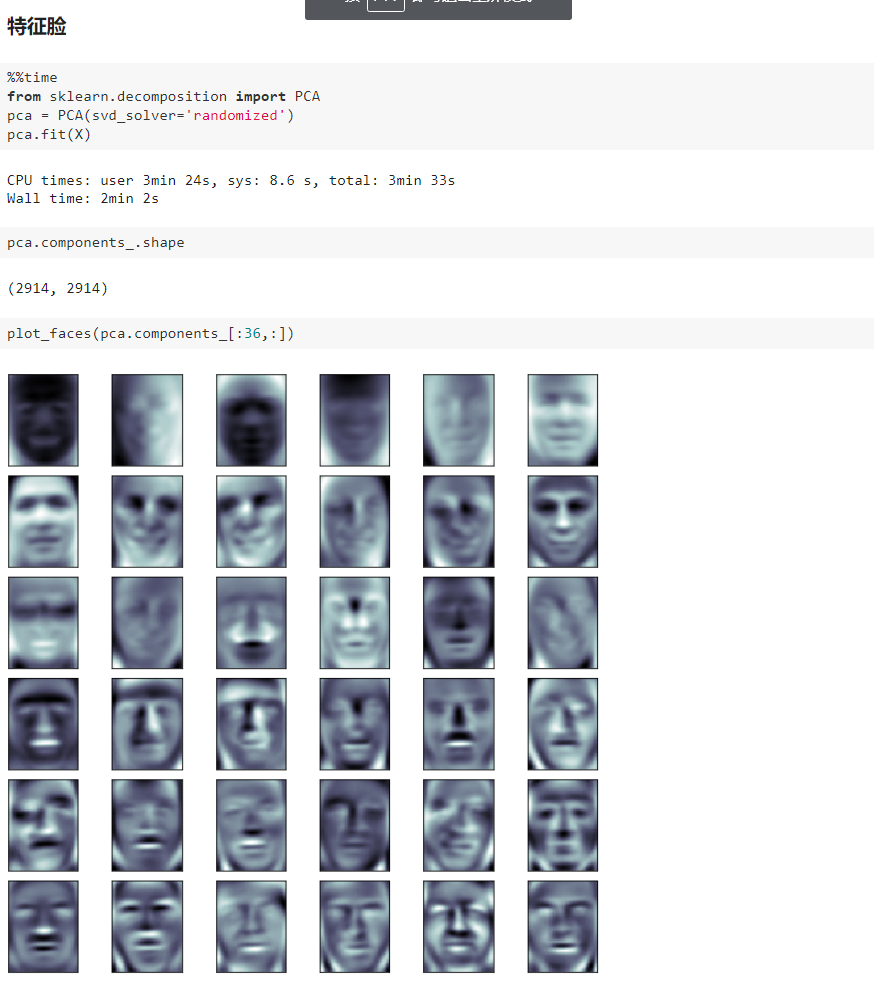
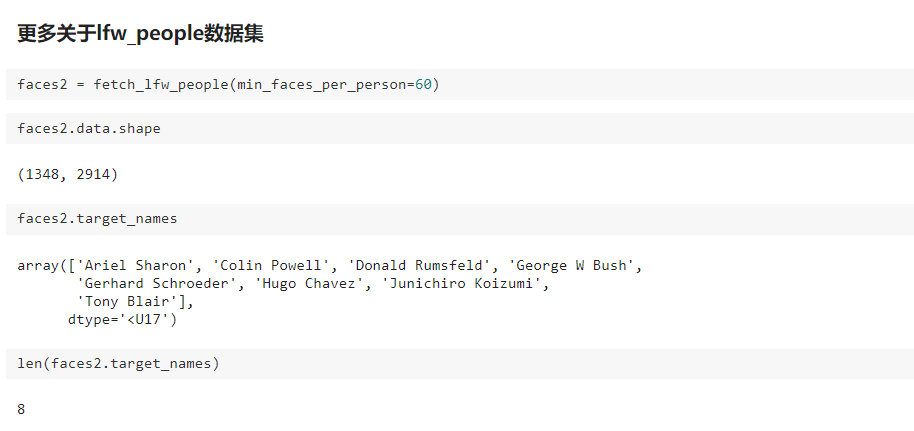
我写的文章只是我自己对bobo老师讲课内容的理解和整理，也只是我自己的弊见。bobo老师的课 是慕课网出品的。欢迎大家一起学习。