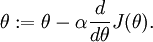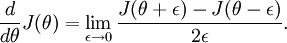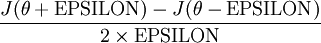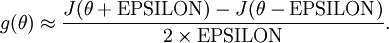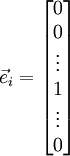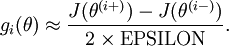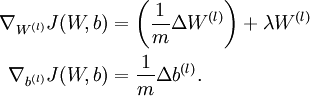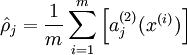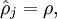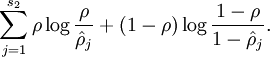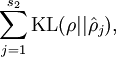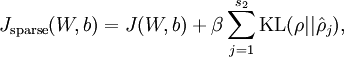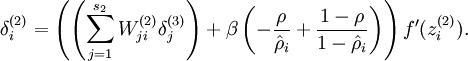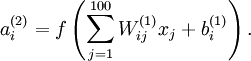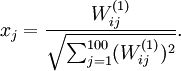Sparse Autoencoder（二）

Gradient checking and advanced optimization

In this section, we describe a method for numerically checking the derivatives computed by your code to make sure that your implementation is correct. Carrying out the derivative checking procedure described here will significantly increase your confidence in the correctness of your code.

Suppose we want to minimize as a function of . For this example, suppose , so that . In this 1-dimensional case, one iteration of gradient descent is given by

Suppose also that we have implemented some function that purportedly computes , so that we implement gradient descent using the update .

Recall the mathematical definition of the derivative as

Thus, at any specific value of , we can numerically approximate the derivative as follows:

Thus, given a function that is supposedly computing , we can now numerically verify its correctness by checking that

The degree to which these two values should approximate each other will depend on the details of . But assuming , you'll usually find that the left- and right-hand sides of the above will agree to at least 4 significant digits (and often many more).

Suppose we have a function that purportedly computes ; we'd like to check if is outputting correct derivative values. Let , where

is the -th basis vector (a vector of the same dimension as , with a "1" in the -th position and "0"s everywhere else). So, is the same as , except its -th element has been incremented by EPSILON. Similarly, let be the corresponding vector with the -th element decreased by EPSILON. We can now numerically verify 's correctness by checking, for each , that:

参数为向量，为了验证每一维的计算正确性，可以控制其他变量

When implementing backpropagation to train a neural network, in a correct implementation we will have that

This result shows that the final block of psuedo-code in Backpropagation Algorithm is indeed implementing gradient descent. To make sure your implementation of gradient descent is correct, it is usually very helpful to use the method described above to numerically compute the derivatives of , and thereby verify that your computations of and are indeed giving the derivatives you want.

Autoencoders and Sparsity

Anautoencoder neural network is an unsupervised learning algorithm that applies backpropagation, setting the target values to be equal to the inputs. I.e., it uses .

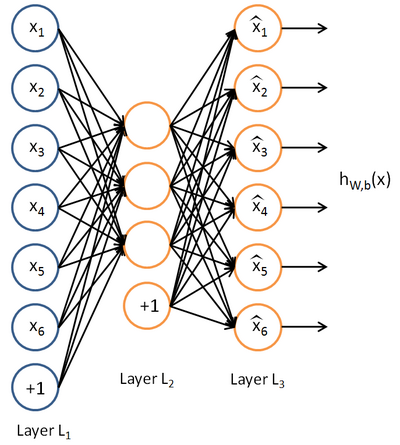
Here is an autoencoder:

we will write to denote the activation of this hidden unit when the network is given a specific input . Further, let

be the average activation of hidden unit (averaged over the training set). We would like to (approximately) enforce the constraint

where is a sparsity parameter, typically a small value close to zero (say ). In other words, we would like the average activation of each hidden neuron to be close to 0.05 (say). To satisfy this constraint, the hidden unit's activations must mostly be near 0.

To achieve this, we will add an extra penalty term to our optimization objective that penalizes deviating significantly from . Many choices of the penalty term will give reasonable results. We will choose the following:

Here, is the number of neurons in the hidden layer, and the index is summing over the hidden units in our network. If you are familiar with the concept of KL divergence, this penalty term is based on it, and can also be written

Our overall cost function is now

where is as defined previously, and controls the weight of the sparsity penalty term. The term (implicitly) depends on also, because it is the average activation of hidden unit , and the activation of a hidden unit depends on the parameters .

Visualizing a Trained Autoencoder

Consider the case of training an autoencoder on images, so that . Each hidden unit computes a function of the input:

We will visualize the function computed by hidden unit ---which depends on the parameters (ignoring the bias term for now)---using a 2D image. In particular, we think of as some non-linear feature of the input

If we suppose that the input is norm constrained by , then one can show (try doing this yourself) that the input which maximally activates hidden unit is given by setting pixel (for all 100 pixels, ) to

By displaying the image formed by these pixel intensity values, we can begin to understand what feature hidden unit is looking for.

对一幅图像进行Autoencoder ，前面的隐藏结点一般捕获的是边缘等初级特征，越靠后隐藏结点捕获的特征语义更深。