expectation-maximization algorithm ---- PRML读书笔记
An elegant and powerful method for finding maximum likelihood solutions for models with latent variables is called the expectation-maximization algorithm, or EM algorithm.
If we assume that the data points are drawn independently from the distribution, then the log of the likelihood function is given by
lnp(X|π,μ,Σ)=Σnln{ΣkπkN(xn|μk,Σk)}
EM for Gaussian Mixtures
Given a Gaussian mixture model, the goal is to maximize the likelihood function with respect to the parameters(comprising the means and covariances of the components
and the mixing coefficients).
1.Initialize the means μk, covariances Σk and mixing coefficients πk, and evaluate the initial value of the log likelihood.
2.E step. Evaluate the responsibilities using the current parameter values
3.M step. Re-estimate the parameters using the current responsibilities.
4.Evaluate the log likelihood
lnp(X|π,μ,Σ)=Σnln{ΣkπkN(xn|μk,Σk)}
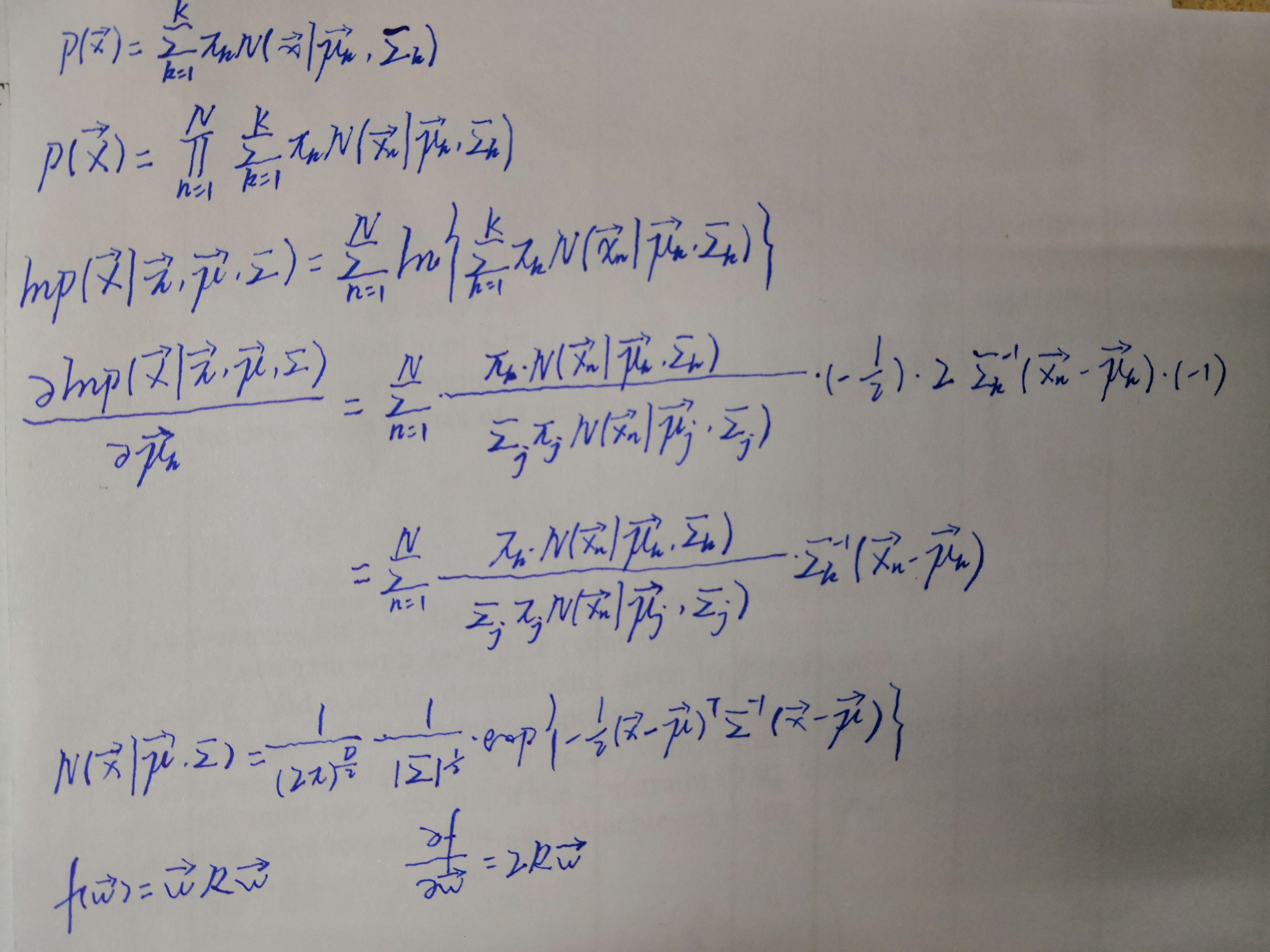
expectation-maximization algorithm ---- PRML读书笔记的更多相关文章
- EM算法(Expectation Maximization Algorithm)
EM算法(Expectation Maximization Algorithm) 1. 前言 这是本人写的第一篇博客(2013年4月5日发在cnblogs上,现在迁移过来),是学习李航老师的< ...
- EM算法(Expectation Maximization Algorithm)初探
1. 通过一个简单的例子直观上理解EM的核心思想 0x1: 问题背景 假设现在有两枚硬币Coin_a和Coin_b,随机抛掷后正面朝上/反面朝上的概率分别是 Coin_a:P1:-P1 Coin_b: ...
- [转]EM算法(Expectation Maximization Algorithm)详解
https://blog.csdn.net/zhihua_oba/article/details/73776553 EM算法(Expectation Maximization Algorithm)详解 ...
- PRML读书笔记——2 Probability Distributions
2.1. Binary Variables 1. Bernoulli distribution, p(x = 1|µ) = µ 2.Binomial distribution + 3.beta dis ...
- PRML读书笔记——3 Linear Models for Regression
Linear Basis Function Models 线性模型的一个关键属性是它是参数的一个线性函数,形式如下: w是参数,x可以是原始的数据,也可以是关于原始数据的一个函数值,这个函数就叫bas ...
- PRML读书笔记——Mathematical notation
x, a vector, and all vectors are assumed to be column vectors. M, denote matrices. xT, a row vcetor, ...
- PRML读书笔记——机器学习导论
什么是模式识别(Pattern Recognition)? 按照Bishop的定义,模式识别就是用机器学习的算法从数据中挖掘出有用的pattern. 人们很早就开始学习如何从大量的数据中发现隐藏在背后 ...
- PRML读书笔记_绪论
一.基本名词 泛化(generalization) 训练集所训练的模型对新数据的适用程度. 监督学习(supervised learning) 训练数据的样本包含输入向量以及对应的目标向量. 分类( ...
- Expectation Maximization Algorithm
期望最大化算法EM. 简介 EM算法即期望最大化算法,由Dempster等人在1976年提出[1].这是一种迭代法,用于求解含有隐变量的最大似然估计.最大后验概率估计问题.至于什么是隐变量,在后面会详 ...
随机推荐
- 移动web——bootstrap如何修改原组件
基本介绍 1.bootstrap提供了丰富的组件,但是有时候我们不仅要删除不必要的标签,还需要修改里面的样式 2.我们建议若是修改样式那么最好将源样式从css中拷贝出来,名字换掉,然后修改具体样式,这 ...
- html5——过渡
transition:1.开始状态 2.终止状态 3.过渡属性 transition: width 2s, background-color 2s;//属性,时间 transition: a ...
- 13、scala模式匹配
1.模式匹配的基础语法 2.对类型进行模式匹配 3.对Array和List的元素进行模式匹配 4.case class与模式匹配 5.Option与模式匹配 1.模式匹配的基础语法 Scala提供了m ...
- Math.floor() 与 parseInt()
parseInt()与Math.floor()都能实现数字的向下取整,但是两者存在根本上的差异,1.Math.floor()用于一个数的向下取整,不能解析字符串 <script type=&qu ...
- BZOJ 4520: [Cqoi2016]K远点对 KDtree + 估价函数 + 堆
Code: #include<bits/stdc++.h> #define ll long long #define maxn 200000 #define inf 10000000000 ...
- swift 再识枚举变量
// Use enum to create an enumeration. Like classes and all other named types, enumerations can have ...
- 2.git进阶篇总结
阅读 Git 原理详解及实用指南 记录 进阶 1 - HEAD.master 与 branch: 介绍了 Git 中的一些「引用」:HEAD.master.branch.这里总结一下: HEAD 是指 ...
- array_map 等php回调函数使用问题(关联数组下标获取)
前言:我自己用此类回调函数,来替代 foreach 纯粹是用为代码的简洁性,让代码更好看.(我有点代码小洁癖~) 1.array_reduce 当迭代处理一个一维索引数组时,在回调函数内是无法获取到当 ...
- windows桌面远程工具连接Ubuntu
1.Ubuntu安装:sudo apt-get install xrdp sudo apt-get install vnc4server sudo apt-get install xubuntu ...
- Keil MDK下如何设置非零初始化变量(复位后变量值不丢失)
一些工控产品,当系统复位后(非上电复位),可能要求保持住复位前RAM中的数据,用来快速恢复现场,或者不至于因瞬间复位而重启现场设备.而keil mdk在默认情况下,任何形式的复位都会将RAM区的非初始 ...
