paxos协议(1)-朴素paxos

前言

学习paxos协议，最困惑我的两点是：

1. 朴素paxos是怎么样的？这部分主要是原理；

2. paxos协议是怎么运用到分布式系统解决问题的。因为很多博客的开篇说paxos协议可以运用在很多地方，如：分布式中的一致性、NoSQL中的数据更新。然而博客中又是以论文中的三个小岛的场景去解释，作为初学者，我没有把该协议解决的问题和算法的步骤联系起来。

1.朴素paxos的提出

paxos解决的是：如何确定一个不可变变量取值问题。比如，我们三个人同时拿笔写东西，我们要用一个协议去约定我们写的东西，使得我们三个写的东西是一样的，而且我们所写的东西不可更改。这时候最大的困惑是：这个和Nosql数据更新怎么联系起来，先不要想它的运用场景，就这个不可变变量的取值问题去理解朴素的paxos算法，之后再去看运用。

（1）如何实现这个系统？

需求：需要一个存储系统，存储一个变量var，这个变量var的取值要么是v，要么是null。一旦这个变量var的取值被确定为v，那么不可改变。

三种角色定义：

Proposer——提出一个proposal（该proposal目前就是就是：把一个值写进系统中）

Acceptor——同意这个proposal

Learner—— 每当一个proposal被Acceptor确定之后，需要Learner知道

方案1：如果Accepter只有一个，我们可以把所有的proposal都发到这个acceptor，它选取收到的第一个proposal并同意proposal即可保证一致性。

问题：Acceptor发生单点故障这个系统就挂了。

方案2: 引入多Acceptor。

P1: 批准者必须批准它收到的第一个议案。但是这样并不能保证所有acceptor接受的是同一个值的proposal。

将proposal编号（这时候proposal有两个信息一个是编号n，一个是数值v），这个proposal有三个状态：被提出(issued)、被接受(accepted)、被最终选定(choosen)。

　 P2:  如果编号n的proposal已经被最终选定，那么高于编号n、被最终选定(choosen)的proposal包含数值v。

P2^a.如果编号n的proposal已经被选择，那么高于编号n、被acceptor接受的proposal包含数值v;

P2^b 如果编号n的proposal已经被选择，那么高于编号n、被proposer提出的proposal包含数值v;

P2^c 对于每一个<n,v>，如果任何一个proposal<n,v>被提出，必须有超过半数的acceptor构成一个集合S，才能够被最终选定，

这个集合S要么满足以下条件(a)，要么满足条件(b).

(a)没有小于编号n的proposal被S中的acceptor接受；

(b)v是S接受过的比n小的提案中号码最大的提案的值;

P2^c=>P2^b=>P2^a=>P2，详情可以参考博文：paxos算法1-算法形成理论。

所以要实现这个系统，需要实现P2^b和p1。

算法执行步骤：

第一阶段：

第二阶段：

用视频中例子来跑这个算法。

a.执行phrase 1(a),发起prepare请求,试图获取访问权,进入phrase1(b)，因为目前还acceptor都没有回复过proposor，所以最大编号的当然是 #1,

并且这时候接收到这个prepare请求的acceptor把 #1作为当前最大编号，不会接收小于这个编号的proposal。

b. 这时候收到半数的回复，进入第二阶段，发送一个accept 请求到多数的acceptor，prase2（a）中说的这个V值怎么取？如果prepare阶段中，acceptor回应中包含了value，则取其编号最大的那个，作为v；如果回应中不包含任何value，则proposer随意选择一个。因为这里是不包含任何value，那么就取Accept<#1,v1>，试图让acceptor接受这个值。按照prase b，这个时候收到的是#1的accept请求，所以它就接受这个accept

c. 按照prase2(a)，收到acceptor对于prepare的回复之后，会向它们发起accept请求，但是在网络中会存在延时的问题，可能发生的情况是p2试图发起prepare请求。这个时候，执行phrase1(b)，这个时候访问权被p2抢占。

d.p2进入prase2，但是这时候恰好p1执行prase2阶段的话，获得#2访问权的acceptor就会把p1发来的accept给refuse掉。这时候p1收到ok，按照prase1(a)，它收到了超过半数的回复，那么实际上它已经是确定性取值了。

e.进入p2的prase2阶段之后，如果prepare阶段中，acceptor回应中包含了value，则取其编号最大的那个，作为v；如果回应中不包含任何value，则proposer随意选择一个。这里p2就是选取编号最大的一个#1，然后accept中带#1对应的value   v1 .

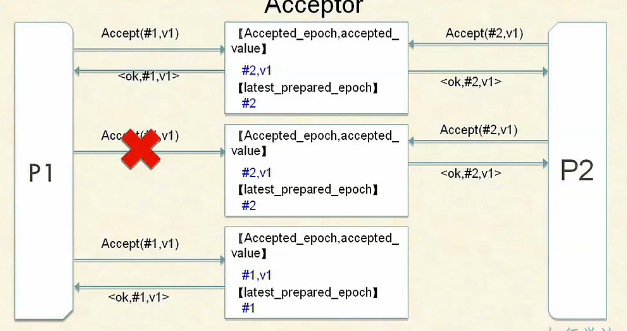
这里p1形成了 确定性取值，v2也形成了确定性取值。如果只有p2形成确定性取值，取值还是v1.

（2）活锁问题

在上面的例子中，如果总是在prase2完成之前，下一个prase1发生，这就是活锁。

（3）唯一编号问题

reference

paxos算法1-算法形成理论

paxos算法和分布式存储系统

Paxos算法2-算法过程

Paxos算法3-实现探讨

paxos-simple^[1]

[1]论文中经常提到拜占庭错误，如果没兴趣了解可以先忽略，不影响paxos的理解