[C++] 分治法之棋盘覆盖、循环赛日程表

一、分治的基本思想

　　将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

　　对于一个规模为 n 的问题，若问题可以容易地解决，则直接解决，否则将其分解为 k 个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

二、用分治法求解问题的主要步骤

　　1、分解：将原问题分解为若干规模较小、相互独立、与原问题形式相同的子问题；

　　2、解决：若子问题规模较小而容易被解决则直接解决，否则，递归地解各个子问题；

　　3、合并：将各子问题的解合并得到原问题的解。

三、分治法实例

　　1、棋盘覆盖

　　在一个 2^k * 2^k 个方格组成的棋盘中，有一个方格与其它的不同，若使用以下四种 L 型骨牌覆盖除这个特殊方格的其它方格，如何覆盖。四个 L 型骨牌如下图：

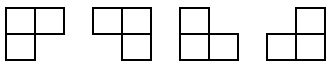
图1.1 L型骨牌

棋盘中的特殊方格如图：

图1.2 存在特殊方格的棋盘

　　覆盖完成后的棋盘：

图1.3 覆盖完成的棋盘

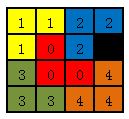
 #include<iostream>
 using namespace std;

 int tile = ;
 int Board[][];    //棋盘 

 /*
 tr:棋盘左上角方格的行号
 tc:棋盘左上角方格的列号
 dr:特殊方格所在的行号
 dc:特殊方格所在的列号
 size:棋盘的规格（size * size)
 */
 void ChessBoard(int tr,int tc , int dr, int  dc, int size)
 {
     if(size == ) return;
     int t =tile++,        //L型骨牌号
         s = size/;        //分割棋盘
     //覆盖左上角子棋盘
     if(dr < tr+s && dc < tc+s)
         //特殊方格在此棋盘中
         ChessBoard(tr,tc,dr,dc,s);
     else
     {    //此棋盘中无特殊方格
         //用t号L型骨牌覆盖右下角
         Board[tr+s-][tc+s-] = t;
         //覆盖其余方格
         ChessBoard(tr,tc,dr,dc,s);
     }

     //覆盖右上角子棋盘
     if(dr < tr+s && dc >= tc+s)
         //特殊方格在此棋盘中
         ChessBoard(tr,tc+s,dr,dc,s);
     else
     {    //此棋盘中无特殊方格
         //用t号L型骨牌覆盖左下角
         Board[tr+s-][tc+s] = t;
         //覆盖其余方格
         ChessBoard(tr,tc+s,tr+s-,tc+s,s);
     }

     //覆盖左下角子棋盘
     if(dr >= tr+s && dc < tc+s)
         //特殊方格在此棋盘中
         ChessBoard(tr+s,tc,dr,dc,s);
     else
     {    //此棋盘中无特殊方格
         //用t号L型骨牌覆盖右上角
         Board[tr+s][tc+s-] = t;
         //覆盖其余方格
         ChessBoard(tr+s,tc,tr+s,tc+s-,s);
     }

     //覆盖右下角子棋盘
     if(dr >= tr+s && dc >= tc+s)
         //特殊方格在此棋盘中
         ChessBoard(tr+s,tc+s,dr,dc,s);
     else
     {    //此棋盘中无特殊方格
         //用t号L型骨牌覆盖左上角
         Board[tr+s][tc+s] = t;
         //覆盖其余方格
         ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
     }

 }

 int main()
 {
     ChessBoard( ,  ,  ,  , );
     //输出覆盖完成后的棋盘
     for(int i =  ; i < ; i++)
     {
         for(int j =  ; j < ; j++)
         {
             cout<<Board[i][j];
         }
         cout<<endl;
     }
     return ;
 }

　　2、循环赛日程表

　　设有 n = 2^k 个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表：

　　　　(1)每个选手必须与其他n-1个选手各赛一次；

　　　　(2)每个选手一天只能参赛一次；

　　　　(3)循环赛在n-1天内结束。

请按此要求将比赛日程表设计成有 n 行和 n-1 列的一个表。在表中的第 i 行，第 j 列处填入第 i 个选手在第 j 天所遇到的选手。其中 1 ≤ i ≤ n，1 ≤ j ≤ n-1。8 个选手的比赛日程表如下图：

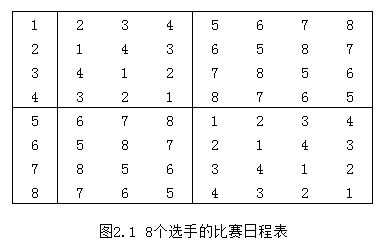
 #include<iostream>
 using namespace std;

 int a[][];
 int n;    //选手的个数

 /*
 tox:目标数组的行号
 toy:目标数组的列号
 fromx:源数组的行号
 fromy:源数组的列号
 r:数组的大小为 r*r
 */
 void Copy(int tox, int toy, int fromx, int fromy, int r)
 {
     for(int i = ; i < r; i++)
         for(int j = ; j < r; j++)
             a[tox+i][toy+j] = a[fromx+i][fromy+j];
 }

 void Table(int k)
 {
     n =  << k;
     //构造正方形表格的第一行数据
     for(int i = ; i < n; i++)
         a[][i] = i + ;
     //采用分治算法，构造整个循环赛日程表
     for(int r = ; r < n; r <<= )
         for(int i = ; i < n; i += *r)
         {
             Copy(r, r + i, , i, r);        //左上角复制到右下角
             Copy(r, i, , r + i, r);        //右上角复制到左下角
         }
 }

 int main()
 {
     int k;
     cout<<"请输入k的值：";
     cin>>k; 

     Table(k);

     for(int i = ; i < n; i++)
     {
         for(int j = ; j < n; j++)
         {
             cout<< a[i][j] << " ";
         }
         cout<<endl;
     }
     return ;
 }