【ZJ选讲·钻石游戏】

N×M的棋盘（M,N<=500）中，每个格子有一个颜色（颜色数1~9）

P次操作（P<=1000），每次给出两个相邻的位置（保证颜色不同，两个格子有一条公共边），把这两个格子交换。

定义每次交换的分值为：通过这次交换能够形成的最大矩形的面积。

求每次操作后的分值。

【题解】

      ①预处理类似于悬线法,维护u,d,l,r

      ②由于需要包含当前点,因此可以向两侧维护单调递减序列(大了就削掉)。

      ③维护双指针,根据单调性，可以O(n)推出最大的矩形面积。

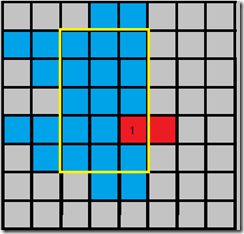（ZJ亲手绘制）

#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 505
using namespace std;
int mp[MAXN][MAXN];
int Up[MAXN][MAXN],Down[MAXN][MAXN],Left[MAXN][MAXN],Right[MAXN][MAXN];
int n,m;
void calculation_row(int i){
	for(int j=1;j<=m;j++)
		if(j==1||mp[i][j-1]!=mp[i][j]) Left[i][j]=1;
			else Left[i][j]=Left[i][j-1]+1;
	for(int j=m;j>=1;j--)
		if(j==m||mp[i][j+1]!=mp[i][j]) Right[i][j]=1;
			else Right[i][j]=Right[i][j+1]+1;
}
void calculation_column(int j){
	for(int i=1;i<=n;i++)
		if(i==1||mp[i-1][j]!=mp[i][j]) Up[i][j]=1;
			else Up[i][j]=Up[i-1][j]+1;
	for(int i=n;i>=1;i--)
		if(i==n||mp[i+1][j]!=mp[i][j]) Down[i][j]=1;
			else Down[i][j]=Down[i+1][j]+1;
}
void readin(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&mp[i][j]);
	for(int i=1;i<=n;i++)
		calculation_row(i);
	for(int j=1;j<=m;j++)
		calculation_column(j);
}
int get_lr(int x,int y,int t[MAXN][MAXN]){
	static int h[MAXN],v[MAXN],cnt,p,ans,now;
	ans=t[x][y];
	cnt=0; p=1; now=t[x][y]; h[++cnt]=t[x][y]; v[cnt]=1;
	for(int i=x-1;i>=x-Up[x][y]+1;i--){
		if(t[i][y]<h[cnt]) h[++cnt]=t[i][y];
		v[cnt]=x-i+1;
	}
	for(int i=x+1;i<=x+Down[x][y]-1;i++){
		now=min(now,t[i][y]);
		while(p+1<=cnt&&h[p+1]>=now) p++;
		ans=max(ans,(i-x+v[p])*now);
	}
	cnt=0; p=1; now=t[x][y]; h[++cnt]=t[x][y]; v[cnt]=1;
	for(int i=x+1;i<=x+Down[x][y]-1;i++){
		if(t[i][y]<h[cnt]) h[++cnt]=t[i][y];
		v[cnt]=i-x+1;
	}
	for(int i=x-1;i>=x-Up[x][y]+1;i--){
		now=min(now,t[i][y]);
		while(p+1<=cnt&&h[p+1]>=now) p++;
		ans=max(ans,(x-i+v[p])*now);
	}
	return ans;
}
int get_ud(int x,int y,int t[MAXN][MAXN]){
	static int h[MAXN],v[MAXN],cnt,p,ans,now;
	ans=t[x][y];
	cnt=0; p=1; now=t[x][y]; h[++cnt]=t[x][y]; v[cnt]=1;
	for(int j=y-1;j>=y-Left[x][y]+1;j--){
		if(t[x][j]<h[cnt]) h[++cnt]=t[x][j];
		v[cnt]=y-j+1;
	}
	for(int j=y+1;j<=y+Right[x][y]-1;j++){
		now=min(now,t[x][j]);
		while(p+1<=cnt&&h[p+1]>=now) p++;
		ans=max(ans,(j-y+v[p])*now);
	}
	cnt=0; p=1; now=t[x][y]; h[++cnt]=t[x][y]; v[cnt]=1;
	for(int j=y+1;j<=y+Right[x][y]-1;j++){
		if(t[x][j]<h[cnt]) h[++cnt]=t[x][j];
		v[cnt]=j-y+1;
	}
	for(int j=y-1;j>=y-Left[x][y]+1;j--){
		now=min(now,t[x][j]);
		while(p+1<=cnt&&h[p+1]>=now) p++;
		ans=max(ans,(y-j+v[p])*now);
	}
	return ans;
}
void printmap(){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++)
			printf("%d ",mp[i][j]);
		printf("\n");
	}

}
void work(){
	int k,x1,x2,y1,y2,ans;
	scanf("%d",&k);
	while(k--){
		ans=0;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		swap(mp[x1][y1],mp[x2][y2]);
		calculation_row(x1);
		calculation_column(y1);
		if(x1==x2){
			calculation_column(y2);
			if(y1>y2) swap(y1,y2);
			ans=max(ans,get_lr(x1,y1,Left));
			ans=max(ans,get_lr(x2,y2,Right));
		}
		else{
			calculation_row(x2);
			if(x1>x2) swap(x1,x2);
			ans=max(ans,get_ud(x1,y1,Up));
			ans=max(ans,get_ud(x2,y2,Down));
		}
		printf("%d\n",ans);
		//printmap();
	}
}
int main(){
	//freopen("2050.in","r",stdin);
	readin();
	work();
	return 0;
}//*ZJ

.