hdu1730Northcott Game(nim博弈)

Northcott Game

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4549    Accepted Submission(s): 2092

Problem Description

　　Tom和Jerry正在玩一种Northcott游戏，可是Tom老是输，因此他怀疑这个游戏是不是有某种必胜策略，郁闷的Tom现在向你求救了，你能帮帮他么？
游戏规则是这样的：
　　如图所示，游戏在一个n行m列（1 ≤ n ≤ 1000且2 ≤ m ≤ 100）的棋盘上进行，每行有一个黑子（黑方）和一个白子（白方）。执黑的一方先行，每次玩家可以移动己方的任何一枚棋子到同一行的任何一个空格上，当然这过程中不许越过该行的敌方棋子。双方轮流移动，直到某一方无法行动为止，移动最后一步的玩家获胜。Tom总是先下（黑方）。图1是某个初始局面，图二是Tom移动一个棋子后的局面（第一行的黑子左移两步）。

图1

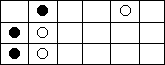
图2

 

Input

　　输入数据有多组。每组数据第一行为两个整数n和m，由空格分开。接下来有n行，每行两个数Ti，Ji (1 ≤ Ti, Ji ≤ m)分别表示Tom和Jerry在该行棋子所处的列数。
　　注意：各组测试数据之间有不定数量的空行。你必须处理到文件末。

 

Output

对于每组测试数据输出一行你的结果。如果当前局面下Tom有必胜策略则输出“I WIN!”，否则输出“BAD LUCK!”。

 

Sample Input

3 6
4 5
1 2
1 2

3 6
4 5
1 3
1 2

 

Sample Output

BAD LUCK!
I WIN!

题意：给出黑子和白子的位置，每个棋子可以在一行中移动到任意位置，但不能越过敌方棋子，知道不能移动为止，最后移动的胜利

题解：emm 相当于nim博弈。每行两颗棋子中间的空格相当于nim博弈中每堆的石子数量（这题的可以移动的空间）。如果中间都没有空格，那肯定先手必败，因为后手可以每步都跟着先手，那先手就只能往一个方向走，不能回退，最后一步肯定是后手走的。而如果反向移动，另一方可以相同方向走相同步数，状态还是没有改变

nim博弈中石子数量的异或和等于1时，先手必胜 。反之，后手必胜

 #include<bits/stdc++.h>
 using namespace std;
 int main() {
     int n,m;
     while(~scanf("%d %d",&n,&m))
     {
         int ans=;
         for(int i=;i<n;i++)
         {
             int a,b;
             scanf("%d %d",&a,&b);
             ans^=abs(b-a)-;    //异或棋子中间的空格数
         }
         if(ans)printf("I WIN!\n");
         else printf("BAD LUCK!\n");
     }
     return ;
 }