【算法】Floyd算法

什么是Floyd

Floyd用于求最短路程。举个栗子，给你一张图，让你求出点【1】到点【5】的最短路程，你会怎么求？

（画图工具：CS Academy）

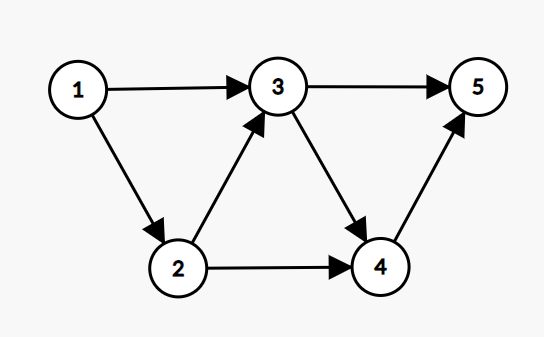
如上图，有向边分别是 1->2  1->3  2->3  2->4  3->4  3->5  4->5

如果一条路一条路去走，可能再这个点数较小的图中能够找到最小路，但是如果有100个点，1000个点呢？

显然不行。

所以，我们就要用到这个“Floyd”了！

学术化来说，Floyd长这样：

Floyd-Warshall算法，中文亦称弗洛伊德算法或佛洛依德算法，是解决任意两点间的最短路径的一种算法，可以正確處理有向圖或负权（但不可存在负权回路）的最短路径問題，同时也被用于计算有向图的传递闭包。（来源于Bing）

额...感觉根本没说什么啊...

好吧，就是解决最短路的一种算法（感觉在说废话）

下面来谈谈Floyd的思维方式吧！

Floyd算法

再来看那张图：

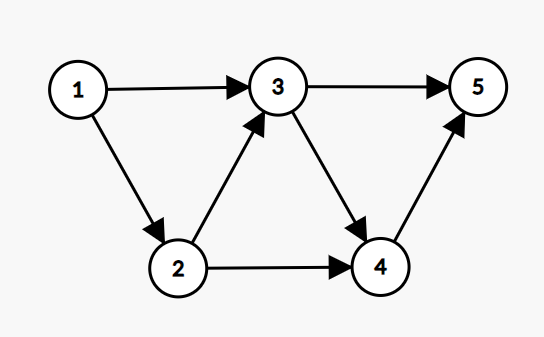
这张图的点数是5，我们要从【1】走到【5】，好像...点数有点多啊...

没关系，我们先来考虑从【1】走到【3】的最短路！

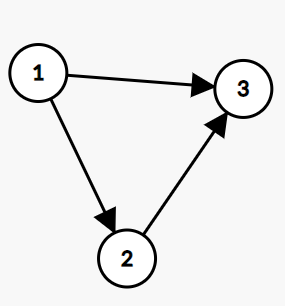
显然，线路一共有【2】条，分别是：

1->2->3

1->(1)->3

这个时候不难发现，从【1】到【3】，我们可以选择经过【2】，也可以直接到【3】（可以理解为经过【1】，【1】与【1】距离为0）

其实，即使是1->4,1->5也是这样的！

也就是说，对于起始点【1】和结束点【5】，只要能通过中间的某个点能形成一条通路，就可以尝试这条路，最后将长度和当前最小长度比较即可！

核心代码

for(int i=1;i<=n;i++){
    for(int j=1;j<=n;j++){
        for(int k=1;k<=n;k++){
            ans=mmap[i][k]+mmap[k][j];
            minn=min(minn,ans);
        }
    }
}            

简单来说，就是找一个“中间点”来判断是否要经过这个点。

写在最后

其实吧，弗洛伊德，真的，不难...