[吴恩达机器学习笔记]13聚类K-means

13.聚类

觉得有用的话,欢迎一起讨论相互学习~Follow Me

13.1无监督学习简介

从监督学习到无监督学习

• 在一个典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正样本和负样本的决策边界，在监督学习中，我们有一系列标签，我们需要据此拟合一个假设函数：
  
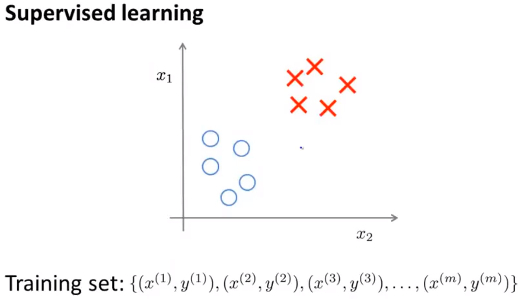
• 与此不同的是，在非监督学习中，我们的数据没有附带任何标签，我们拿到的数据就是这样的：
  

• 在这里我们有一系列点，却没有标签。因此，我们的训练集可以写成只有x(1),x(2),x(3)...一直到x(m),而没有任何标签y.因此，图上画的这些点没有标签信息。也就是说，在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。 图上的数据看起来可以分成两个分开的点集（称为簇），一个能够找到我圈出的这些点集的算法，就被称为聚类算法。

  聚类算法的应用

• 市场分割 ：也许你在数据库中存储了许多客户的信息，而你希望将他们分成不同的客户群，这样你可以对不同类型的客户分别销售产品或者分别提供更适合的服务。
• 社交网络分析 ： 社交网络，例如 Facebook， Google+，或者是其他的一些信息，比如说：你经常跟哪些人联系，而这些人又经常给哪些人发邮件，由此找到关系密切的人群。因此，这可能需要另一个聚类算法，你希望用它发现社交网络中关系密切的朋友。
• 优化网络集群结构 ： 使用聚类算法能够更好的组织计算机集群，或者更好的管理数据中心。因为如果你知道数据中心，那些计算机经常协作工作。那么，你可以重新分配资源，重新布局网络。由此优化数据中心，优化数据通信。

• 了解银河系的构成

---

13.2K均值算法 K-Means Algorithm

• K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组

  算法步骤综述

• K-均值是一个迭代算法，假设我们想要将数据聚类成n个组，其方法为:

1. 首先选择k个随机的点，称为聚类中心(cluster centroids);
2. 簇分配(cluster assignment) 对于数据集中的每一个数据，按照距离K个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。
3. 移动聚类中心(move centroids) 计算 每一个组 的平均值，将该组所关联的中心点移动到平均值的位置。

4. 重复步骤 2-4 直至中心点不再变化。

   步骤详解

• 假设我有如图下方的无标签的数据集，并且想将其分为 两个簇(clusters)即K=2
  

1. 第一步是随机生成 两点(K点，可改变)，这两点被称为 聚类中心(cluster centroids)
   
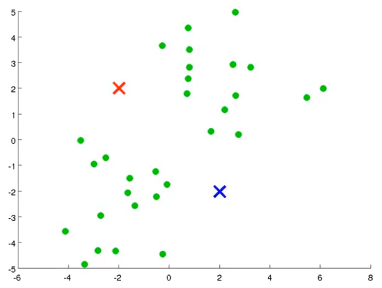
2. 簇分配(cluster assignment) 遍历每个样本，然后根据样本到两个不同的聚类中心的距离哪个更近，来将每个数据点分配给两个聚类中心之一，使用\(||x^{(i)}-u_{k}||^{2}\)来计算距离,其中\(x^{(i)}\)表示无标签的样本点，u_{k}表示 簇中心
   
3. 移动聚类中心(move centroids) 将聚类中心分别移动到各自簇的中心处。即图中 计算所有红点均值 ，然后将红色聚类中心点移动至均值处，蓝色点同理。
   
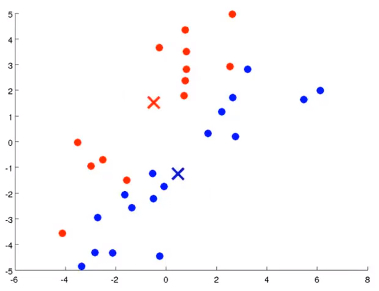
4. 重复2-3过程，直到聚类中心不再移动
   

• K-means算法接收两个输入，一个是 K值即聚类中簇的个数， 一个是 一系列无标签的数据，使用N维向量X表示
  

  算法图示

  

  分离没有明显边界的数据

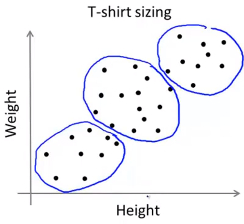
  K-均值算法也可以很便利地用于将数据分为许多不同组，即使在没有非常明显区分的组群的情况下也可以。下图所示的数据集包含身高和体重两项特征构成的，利用 K-均值算法将数据分为三类，用于帮助确定将要生产的 T-恤衫的三种尺寸。
  

---

13.3K均值算法损失函数 K-Means optimization objective

定义损失函数变量

1. 假设有K个簇，\(c^{(i)}\) 表示样本\(x^{(i)}\) 当前所属的簇的索引编号 ，\(c^{(i)}\in(1,2,3...K)\)
2. \(\mu_k\) 表示 第k个聚类中心 的位置，其中 \(k\in{1,2,3,4...K}\)

3. 根据以上定义:则\(\mu_{c^{(i)}}\) 表示样本\(x^{(i)}\)所属簇的中心的 位置坐标

   K-means算法的优化目标

• 损失函数为 每个样本到其所属簇的中心的距离和的平均值 ，优化函数的输入参数为 每个样本所属的簇的编号\(c^{(i)}\)和每个簇中心的坐标\(\mu_{k}\) 这两个都是在聚类过程中不断变化的变量。此代价函数也被称为 畸变函数(Distortion function)
  

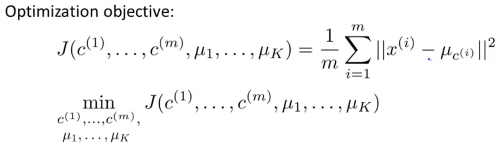
  K-means算法步骤与优化函数

• 对于K-means算法中的 簇分配(将每个样本点分配到距离最近的簇) 的步骤实际上就是在最小化代价函数J，即在\(\mu_1,\mu_2,\mu_3,\mu_4...\mu_K\)固定的条件下调整 \(c^{(1)},c^{(2)},c^{(3)},...c^{(m)}\)的值以使损失函数的值最小。

• 对于K-means算法中的 移动聚类中心(将聚类中心移动到分配样本簇的平均值处) ，即在\(c^{(1)},c^{(2)},c^{(3)},...c^{(m)}\)固定的条件下调整 \(\mu_1,\mu_2,\mu_3,\mu_4...\mu_K\)的值以使损失函数的值最小。
  

---

13.4K均值算法簇中心的随机初始化 Random initialization

随机初始化遵循法则

1. 我们应该选择 K小于m，即聚类中心点的个数要小于所有训练集实例的数量

2. 随机选择 K 个训练实例，然后令 K 个聚类中心分别与这 K 个训练实例相等

   随机初始化的局限性

• 以下两种都是随机初始化的结果，发现随机初始化很容易把 初始化簇中心 分到相近的样本中，这种初始化方式有其局限性。
  

• K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。
  

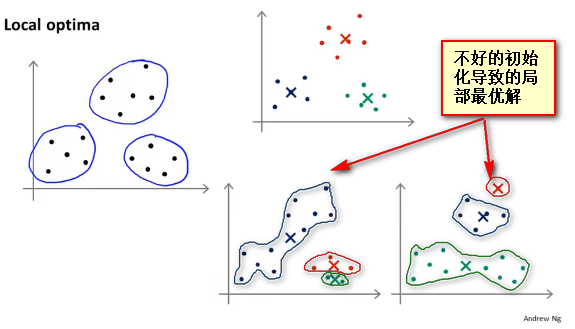
  改进初始化方式--多次随机初始化

• 假如随机初始化K-means算法100 (一般是50-1000) 次之间，每次都使用不同的随机初始化方式，然后运行K-means算法，得到100种不同的聚类方式，都计算其损失函数，选取代价最小的聚类方式作为最终的聚类方式。

• 这种方法在 K 较小的时候（2--10）还是可行的，但是如果 K 较大，这么做也可能不会有明显地改善。(不同初始化方式得到的结果趋于一致)

---

13.5K均值算法聚类数K的选择 Choosing the Number of Cluters

• 没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题，人工进行选择的。选择的时候思考我们运用 K-均值算法聚类的动机是什么，然后选择能最好服务于该目的标聚类数。

  肘部法则(Elbow method)

• 改变聚类数K，然后进行聚类，计算损失函数，拐点处即为推荐的聚类数 (即通过此点后，聚类数的增大也不会对损失函数的下降带来很大的影响，所以会选择拐点)
  

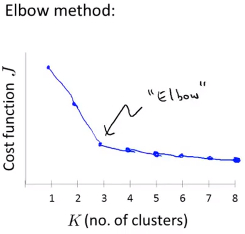
• 但是也有损失函数随着K的增大平缓下降的例子，此时通过肘部法则选择K的值就不是一个很有效的方法了(下图中的拐点不明显，k=3,4,5有类似的功能)
  

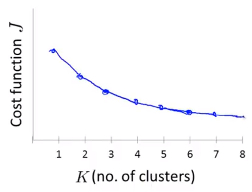
  目标法则)

• 通常K均值聚类是为下一步操作做准备，例如：市场分割，社交网络分析，网络集群优化 ，下一步的操作都能给你一些评价指标，那么决定聚类的数量更好的方式是：看哪个聚类数量能更好的应用于后续目的

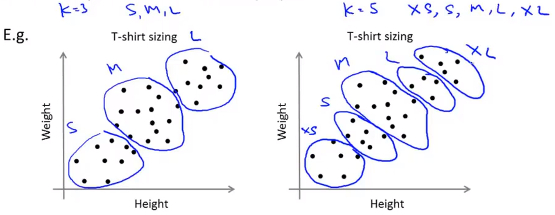
  示例

• 例如对于T恤衫的尺码进行聚类的方法，如左图将其聚为3类(S,M,L)，右图将其聚为5类(XS,S,M,L,XL)进行表示，这两种聚类都是可行的，我们可以 根据聚类后用户的满意程度或者是市场的销售额来决定最终的聚类数量