loj #6515. 「雅礼集训 2018 Day10」贪玩蓝月

\(\color{#0066ff}{输入样例}\)

0
11 10
QU 0 0
QU 1 9
IG 14 7
IF 3 5
QU 0 9
IG 1 8
DF
QU 0 4
IF 1 2
DG
QU 2 9

\(\color{#0066ff}{输出样例}\)

0
-1
12
8
9

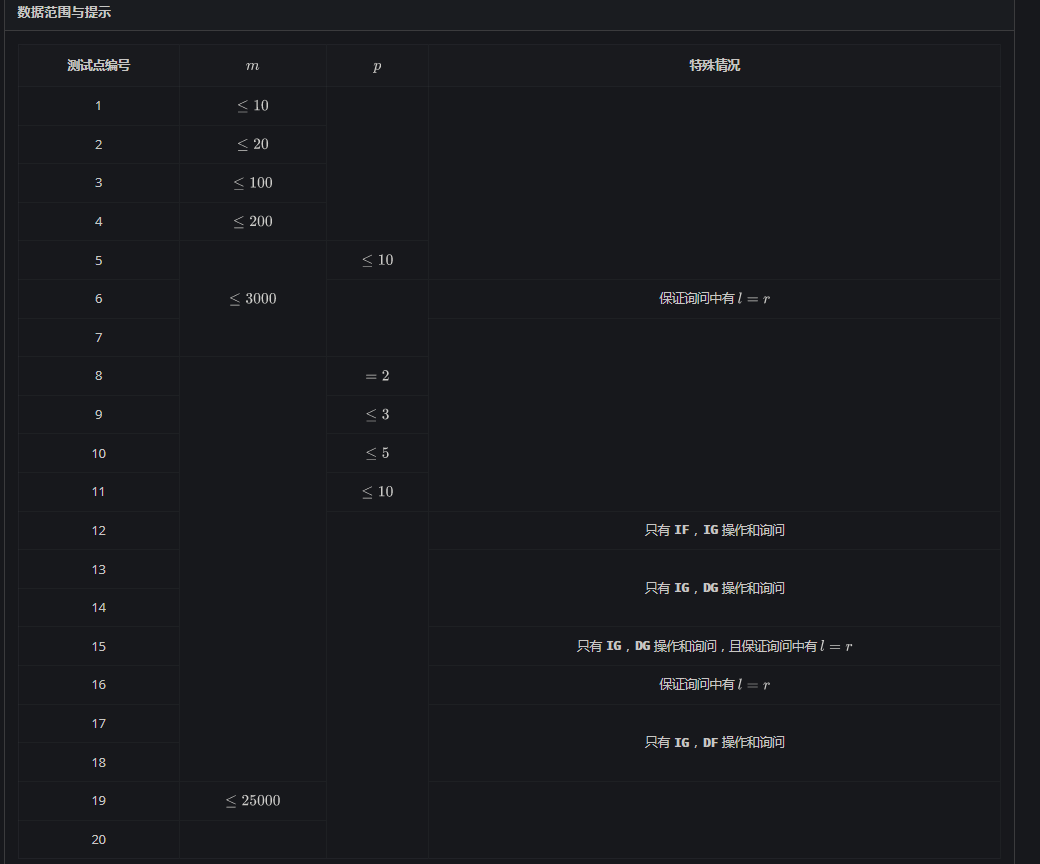
\(\color{#0066ff}{数据范围与提示}\)

\(\color{#0066ff}{题解}\)

维护两个栈，一个是前面插入，一个是后面插入，每次插入的时候跑一遍背包

删除的时候，如果一个栈空了，那么把另一个栈的一半弄过来（保证复杂度），暴力处理一下DP

对于询问，对于每一个\(x\in[1,mod]\)，我们可以找到一个区间使得\([(L+x)\%mod,(R+x)\%mod]就是给的询问的[l,r]\)

我们只需要一个栈的DP数组的x位置的值和另一个数组一段区间的最大值，用这个更新答案就行

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
template<typename T> T chkmax(T &a, const T &b) { return a < b? a = b : b; }
template<typename T> T chkmin(T &a, const T &b) { return a < b? a : a = b; }
const int maxn = 5e4 + 10;
const int maxm = 505;
LL st[maxn][20], f[2][maxn][maxm];
int top[2], mod, lg[maxn], inf;
std::pair<LL, LL> t[2][maxn];
char opt[22];
void predoit() {
	memset(f, 0xcf, sizeof f);
	inf = -f[0][0][0];
	f[0][0][0] = f[1][0][0] = 0;
	lg[0] = -1;
	for(int i = 1; i < maxn; i++) lg[i] = lg[i >> 1] + 1;
}
void ins(bool k, int now, std::pair<LL, LL> mp) {
	t[k][now] = mp;
	for(int i = 0; i < mod; i++) f[k][now][i] = f[k][now - 1][i];
	for(int i = 0; i < mod; i++) chkmax(f[k][now][(i + mp.first) % mod], f[k][now - 1][i] + mp.second);
}
void del(bool k) {
	if(top[k]) return (void)(top[k]--);
	int mid = (top[k ^ 1] + 1) >> 1;
	for(int i = 1; i <= mid; i++) t[k][mid - i + 1] = t[k ^ 1][i], t[k ^ 1][i] = t[k ^ 1][i + mid];
	top[k] = mid - 1, top[k ^ 1] = top[k ^ 1] & 1? mid - 1 : mid;
	for(int i = 1; i <= top[k]; i++) ins(k, i, t[k][i]);
	for(int i = 1; i <= top[k ^ 1]; i++) ins(k ^ 1, i, t[k ^ 1][i]);
}
LL getans(int l, int r) {
	int len = lg[r - l + 1];
	return std::max(st[l][len], st[r - (1 << len) + 1][len]);
}

LL query(int l, int r) {
	LL ans = -inf;
	for(int i = 0; i < mod; i++) st[i][0] = f[0][top[0]][i];
	for(int j = 1; j <= lg[mod]; j++)
		for(int i = 0; i + (1 << j) <= mod; i++)
			st[i][j] = std::max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
	for(int i = 0; i < mod; i++) {
		if(f[1][top[1]][i] < 0) continue;
		int L = l - i, R = r - i;
		(L += mod) %= mod, (R += mod) %= mod;
		if(L <= R) chkmax(ans, f[1][top[1]][i] + getans(L, R));
		else chkmax(ans, f[1][top[1]][i] + std::max(getans(L, mod - 1), getans(0, R)));
	}
	return ans < 0? -1 : ans;
};

int main() {
	in(); int T = in(); LL x, y; mod = in();
	predoit();
	while(T --> 0) {
		scanf("%s", opt);
		if(opt[0] == 'I') x = in(), y = in(), ins(opt[1] == 'G', ++top[opt[1] == 'G'], std::make_pair(x % mod, y));
		if(opt[0] == 'D') del(opt[1] == 'G');
		if(opt[0] == 'Q') x = in(), y = in(), printf("%lld\n", query(x, y));
	}
	return 0;
}