OpenCV学习(8) 分水岭算法(2)

    现在我们看看OpenCV中如何使用分水岭算法。

    首先我们打开一副图像：

   // 打开另一幅图像
  cv::Mat    image= cv::imread("../tower.jpg");
    if (!image.data)
        {
        cout<<"不能打开图像！"<<endl;
        return 0;
        }

     接下来，我们要创建mark图像。mark图像格式是有符号整数，其中没有被mark的部分用0表示，其它不同区域的mark标记，我们用非零值表示，通常为1-255，但也可以为其它值，比如大于255的值，不同mark区域甚至可以用同样的值，这个值大小对最后分割可能没有影响(也可能影响)，最好不同mark区域还是用不同的值表示，这样能够确保结果正确，之所以用有符号整数，是因为opencv在分水岭算法内部，要用-1，-2等来标记注水区域，最终在mark图像中生成的分水岭线就是用-1表示。

    我们通常会创建uchar格式的灰度图，指定mark区域，然后转化为有符号整数的图像格式。

    首先对整个背景区域我们创建一个mark域，是下图中白色框框住的部分，其灰度值为255，第二个选择mark域为塔，就是黑色框框住的一块区域，其灰度值为64，最后就是树mark域，蓝色框的部分，其灰度值为128。在分水岭算法时候，会分别对这个3个区域来进行注水操作，如果两个注水盆地被一个mark域覆盖，则它们之间不会有分水岭线产生。

    对于mark图像，opencv分水岭算法在初始化时候，会把最外圈的值置为-1，作为整个图像的边界，所以我们第一个mark区域，选择倒数第2外圈，因为设置到最外圈，最后还是会被冲掉。

// 标示背景图像
cv::Mat imageMask(image.size(),CV_8U,cv::Scalar(0));

cv::rectangle(imageMask,cv::Point(1,1),cv::Point(image.cols-2,image.rows-2),cv::Scalar(255),1);
// 表示塔
cv::rectangle(imageMask,cv::Point(image.cols/2-10,image.rows/2-10),
    cv::Point(image.cols/2+10,image.rows/2+10),cv::Scalar(64),10);
//树
cv::rectangle(imageMask,cv::Point(64,284),
    cv::Point(68,300),cv::Scalar(128),5);

mark图像：

 

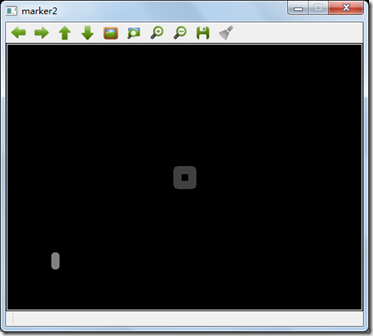
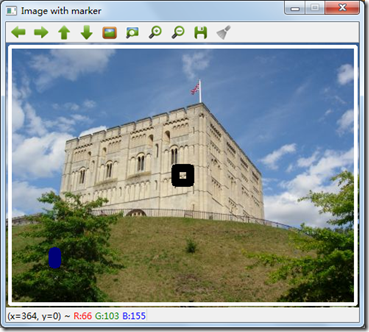
   注意：mark图像是32bit的有符号整数，所以在使用分水岭算法前，我们先对mark图像做一个转化。算法执行完后，再转化为0-255的灰度图。

  imageMask.convertTo(imageMask,CV_32S);
    // 设置marker和处理图像 
  cv::watershed(image,imageMask);

  cv::Mat mark1;
  imageMask.convertTo(mark1,CV_8U);
  cv::namedWindow("marker");

   cv::imshow("marker",mark1);

    此时imageMask图像从无符号整数转化为uchar后，如下图所示，第一个mask区域注水，将会使得整个图像为白色，之后分别在第二个，第三个区域的盆地注水，会产生相应的注水图，注水的区域的值即为mark的值，128和64, 分水岭线则为0，注：在转化前分水岭线的值为-1，转化后成为0。

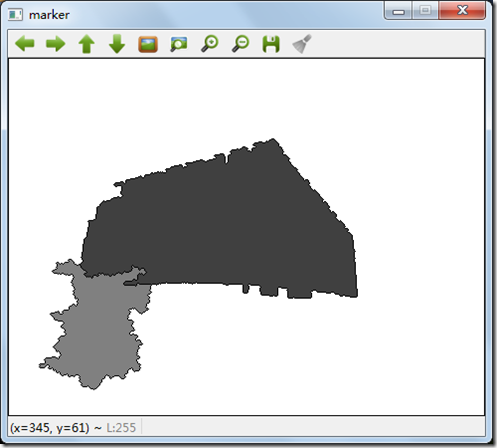
我们使用一个转化函数把分水岭线转化为黑色，其它的部分都白黑色，转化函数的公式为：

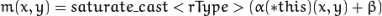
imageMask(x,y) = saturate_cast<uchar>(255*imageMask(x,y)+255)
  imageMask.convertTo(imageMask,CV_8U,255, 255);

  最后显示分水岭线，得到下图：(注：在转化前，分水岭线的值为-1)

 

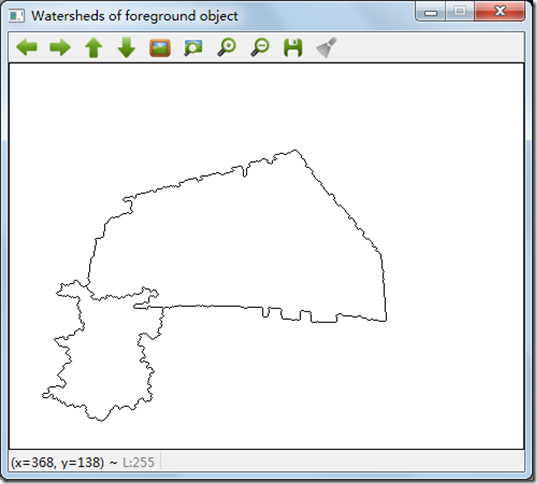
源码：工程FirstOpenCV7

下载：稍后提供