BZOJ 2627 JZPKIL

题目链接：http://www.lydsy.com:808/JudgeOnline/problem.php?id=2627

题意：计算下面式子

思路：

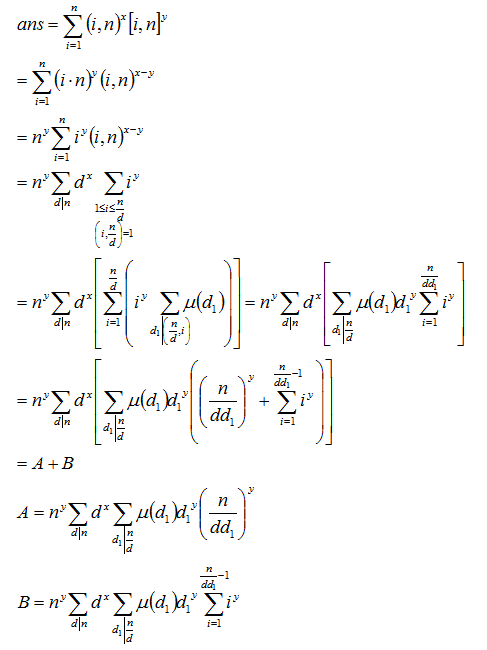
A先不管。我们来搞B部分。下面说如何计算B这个最后那部分

伯努利函数：

所以

带入到B中

那个f(k)中k一旦确定x,y,k就是常数，所以就是关于n的函数。

因为d^x以及莫比乌斯函数都是积性函数，而g是他们的狄利克雷卷积，所以g也是积性函数。所以依次计算每个n的质因子即可。

这样我们计算每个质因数即可。现在我们计算g(p^s)

我们发现

所以

这样我们就计算出上面的B，即

那么还剩A，我们发现A=f(1)。

这样就全部搞定。这道题涉及组合数、伯努利数以及大素数的判定分解。

const i64 mod=1000000007;
const int N=3005;

i64 exGcd(i64 a,i64 b,i64 &x,i64 &y)
{
    i64 r,t;
    if(b==0)
   {
       x=1;
       y=0;
       return a;
   }
   r=exGcd(b,a%b,x,y);
   t=x;
   x=y;
   y=t-a/b*y;
   return r;
}

i64 reverse(i64 a,i64 b)
{
    i64 x,y;
    exGcd(a,b,x,y);
    if(x<0) x+=mod;
    return x;
}

int C[N][N],p[N],pInv[N],B[N],T[N][N];
int prime[N],primeNum,tag[N];

void init()
{
    p[0]=pInv[0]=1;
    for(int i=1;i<N;i++)
    {
        p[i]=(i64)p[i-1]*i%mod;
        pInv[i]=reverse(p[i],mod);
    }
    C[0][0]=1;
    for(int i=1;i<N;i++)
    {
        C[i][0]=C[i][i]=1;
        for(int j=1;j<i;j++)
        {
            C[i][j]=C[i-1][j-1]+C[i-1][j];
            if(C[i][j]>=mod) C[i][j]-=mod;
        }
    }
    B[0]=1;
    for(int i=1;i<N;i++)
    {
        B[i]=0;
        for(int j=0;j<i;j++)
        {
            B[i]-=(i64)C[i+1][j]*B[j]%mod;
            if(B[i]<0) B[i]+=mod;
        }
        B[i]=B[i]*reverse(C[i+1][i],mod)%mod;
    }
    for(int i=0;i<N;i++)
    {
        i64 a=reverse(i+1,mod);
        for(int j=0;j<=i;j++)
        {
            T[i][j]=a*B[j]%mod*C[i+1][j]%mod;
        }
    }
    for(int i=2;i<N;i++) if(!tag[i])
    {
        prime[primeNum++]=i;
        for(int j=i+i;j<N;j+=i) tag[j]=1;
    }
}

i64 Gcd(i64 x,i64 y)
{
    if(!y) return x;
    return Gcd(y,x%y);
}

i64 mul(i64 x,i64 y,i64 mod)
{
    i64 ans=0;
    while(y)
    {
        if(y&1)
        {
            ans+=x;
            if(ans>=mod) ans-=mod;
        }
        x<<=1;
        if(x>=mod) x-=mod;
        y>>=1;
    }
    return ans;
}

i64 myPow(i64 a,i64 b,i64 mod)
{
    i64 ans=1;
    while(b)
    {
        if(b&1) ans=mul(ans,a,mod);
        a=mul(a,a,mod);
        b>>=1;
    }
    return ans;
}

i64 myPow(i64 a,i64 b)
{
    a%=mod;
    i64 ans=1;
    while(b)
    {
        if(b&1)
        {
            ans*=a;
            if(ans>=mod) ans%=mod;
        }
        a*=a;
        if(a>=mod) a%=mod;
        b>>=1;
    }
    return ans;
}

void cal1(i64 n,int x,int y)
{
    if(0==x)
    {
        printf("%lld\n",n%mod);
        return;
    }
    i64 ans=0,p=(n+1)%mod,tmp=p;
    for(int i=y;i>=0;i--)
    {
        ans+=T[y][i]*tmp;
        ans%=mod;
        tmp=tmp*p%mod;
    }
    ans=ans*myPow(n,y)%mod;
    if(ans<0) ans+=mod;
    printf("%lld\n",ans);
}

i64 all[N];
int allNum;

int witness(i64 a,i64 n)
{
    i64 m=n-1,x,y,k=0;
    while(!(m&1)) k++,m>>=1;
    x=myPow(a,m,n);
    while(k--)
    {
        y=mul(x,x,n);
        if(1==y&&x!=1&&x!=n-1) return 1;
        x=y;
    }
    return y!=1;
}

int isPrime(i64 n)
{
    if(2==n) return 1;
    if(!(n&1)) return 0;
    if(1==n) return 0;

    int cnt=17;
    while(cnt--)
    {
        i64 a=rand()%(n-1)+1;
        if(witness(a,n)) return 0;
    }
    return 1;
}

i64 pollard(i64 n,int c)
{
    i64 x=1,y=1,d,k=2,i=1;
    while(1)
    {
        x=mul(x,x,n)+c;
        d=Gcd(abs(y-x),n);
        if(d>1&&d<n) return d;
        if(y==x) return n;
        if(++i==k) y=x,k<<=1;
    }
}

void split(i64 n)
{
    if(1==n) return;
    if(isPrime(n))
    {
        all[++allNum]=n;
        return;
    }
    i64 m=n;
    int c=1;
    while(m==n) m=pollard(m,++c);
    split(m);
    split(n/m);
}

struct node
{
    int primeNum;
    i64 p[N];
    int num[N];
    i64 po[N];
}A;

i64 pw[100][100],pw1[100];

i64 get(i64 i,int y)
{
    i64 tmp=1;
    for(int j=1;j<=A.primeNum;j++)
    {
        i64 S1=0,S2=0;
        i64 a=myPow(A.p[j],y);
        i64 b=myPow(A.p[j],y+1-i);
        pw1[0]=1;
        for(int k=1;k<=A.num[j];k++)
        {
            pw1[k]=pw1[k-1]*b;
            if(pw1[k]>=mod) pw1[k]%=mod;
        }
        for(int k=0;k<=A.num[j];k++)
        {
            S1+=pw[j][k]*pw1[A.num[j]-k];
            if(S1>=mod) S1%=mod;
        }
        for(int k=0;k<A.num[j];k++)
        {
            S2+=pw[j][k]*pw1[A.num[j]-k-1]%mod*a;
            if(S2>=mod) S2%=mod;
        }
        S1-=S2;
        S1%=mod;
        if(S1<0) S1+=mod;
        tmp=tmp*S1;
        if(tmp>=mod) tmp%=mod;
        tmp=tmp*myPow(A.po[j],y);
        if(tmp>=mod) tmp%=mod;
    }
    return tmp;
}

void cal2(i64 n,int x,int y)
{
    allNum=0;
    for(int i=0;i<primeNum;i++)
    {
        while(0==n%prime[i])
        {
            all[++allNum]=prime[i];
            n/=prime[i];
        }
    }
    if(n>1) split(n);
    sort(all+1,all+allNum+1);
    A.primeNum=1;
    A.p[1]=all[1];
    A.num[1]=1;
    A.po[1]=all[1];
    for(int i=2;i<=allNum;i++)
    {
        if(all[i]==all[i-1])
        {
            A.num[A.primeNum]++;
            A.po[A.primeNum]*=all[i];
        }
        else
        {
            A.primeNum++;
            A.p[A.primeNum]=all[i];
            A.num[A.primeNum]=1;
            A.po[A.primeNum]=all[i];
        }
    }
    for(int i=1;i<=A.primeNum;i++)
    {
        pw[i][0]=1;
        i64 a=myPow(A.p[i],x);
        for(int j=1;j<=A.num[i];j++)
        {
            pw[i][j]=pw[i][j-1]*a;
            if(pw[i][j]>=mod) pw[i][j]%=mod;
        }
    }

    i64 ans=0;
    for(int i=0;i<=y;i++)
    {
        ans+=get(i,y)*T[y][i];
        ans%=mod;
    }
    if(y>0) ans+=get(1,y),ans%=mod;
    if(ans<0) ans+=mod;
    printf("%lld\n",ans);
}

int main()
{

    init();
    int T=myInt();
    while(T--)
    {
        i64 n;
        int x,y;
        scanf("%lld%d%d",&n,&x,&y);
        if(x==y) cal1(n,x,y);
        else cal2(n,x,y);
    }
}