【5】KMP学习笔记

前言

WFLS 2023 寒假集训 Day1

KMP好闪，拜谢KMP！

暴力算法

单模字符串匹配算法

设 \(i\) 为主串 \(s\)（文本串）指针，\(j\) 为子串 \(t\)（模式串）指针，最开始 \(i,j\) 都从 \(0\) 开始，如果 \(s[i]==t[j]\) 那么 \(i++\) ， \(j++\) 。否则匹配失败（失配），则 \(i=i-j+1\) ， \(j=0\) 。

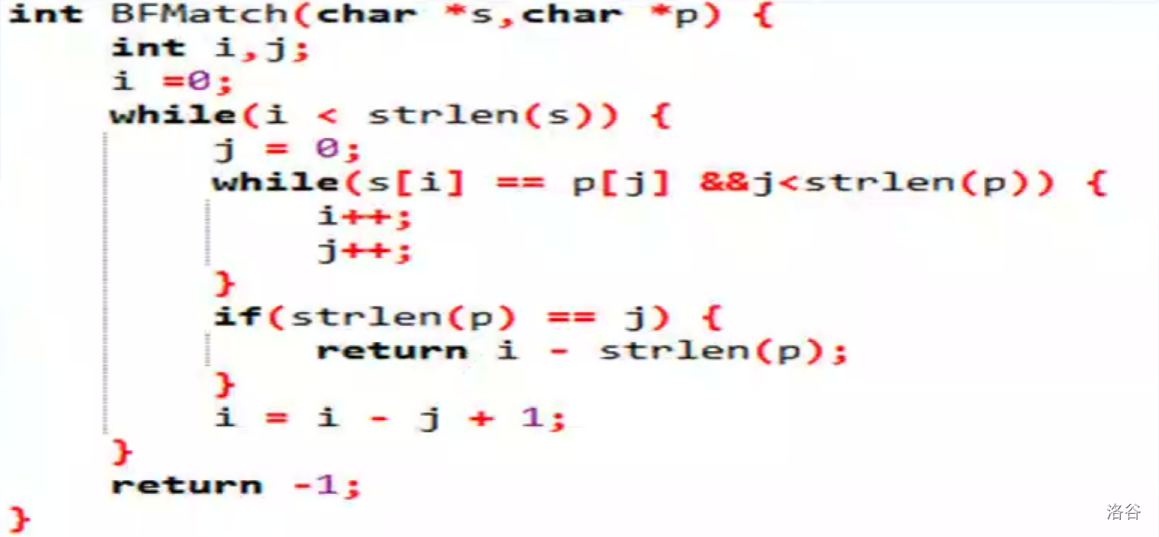
时间复杂度： \(O(mn)\)

KMP

首先我们要思考，暴力算法慢在哪里。

最主要的问题，就是这一句话:

i=i-j+1;

有没有办法可以使主指针 \(i\) 不回溯呢？

next数组

如果匹配到 \(t[j]\) 时失配，那么前 \(j-1\) 项肯定匹配。

这时就要考虑使用模式串自身的性质了。

举个例子：

asbhguwsdwqqddwsdwsdwsr
      wsdwsr
      ^   ^
      i   j

此时在 \(j\) 处失配了，但是根据观察，我们可以把模式串挪到下面位置，从而减少运算量。

asbhguwsdwqqddwsdwsdwsr
         wsdwsr
         ^
        i,j

由于在模式串中的前 \(j-1\) 项已经匹配了，所以我们可以在前 \(j-1\) 项中找到一个前缀，使其与后面第 \(j\) 项之前的某一段相同，然后就可以直接跳到这一段，继续进行匹配。

这是就要引入一个概念了：最大公共前缀

其实就是上面说的 一个前缀 ，在进行KMP算法时，可以把每个 \(j\) 的最大公共前缀存进一个表中，这个表就是next数组。

例如字符串 wsdwsr 的next数组

	w	s	d	w	s	r
\(next[j]\)	\(-1\)	\(0\)	\(0\)	\(0\)	\(1\)	\(2\)

求next数组的方法：

设现在算到了第 \(n\) 位

\(1\) ：第一位的next值为 \(-1\)

\(2\) ：查看第 \(n-1\) 位的next值，记为 \(a\)

\(3\) ：判断 \(a\) 是否为 \(-1\) ，如果 \(a\) 为 \(-1\) ，则 \(next[n]=0\)

\(4\) ：否则将第 \(n-1\) 个字符与第 \(a\) 个字符进行比较

\(5\) ：若相同，则 \(next[n]=a+1\)

\(6\) ：若不相同，则令 \(a=next[a]\) ，执行第 \(3\) 步。

计算完毕后，\(next[n]\) 就表示前 \(n-1\) 个字符的最大公共前缀。

模板如下：

int getnext(char t[],int next[])
{
	int i=0,j=-1,res=-2;
	next[0]=-1;
	int l=strlen(t);
	while(i<l)
	     {
	     	if(j==-1||t[i]==t[j])
	     	   {
	     	   	i++;
	     	   	j++;
	     	   	next[i]=j;
			   }
			else j=next[j];
		 }
	for(int i=0;i<l;i++)
	    res=max(res,next[i]);
	return res;
}

单模字符串匹配

有了 \(next\) 表，在匹配过程中如果失配，我们可以直接令 \(j=next[j]\) ，查表跳转到最大公共前缀的后一个位置就行了。

模板如下：

int kmp(char s[],char t[],int next[])
{
	int i=0,j=0,cnt=0;
	int ls=strlen(s),lt=strlen(t);
	while(i<ls)
	      {
	      	if(j==-1||s[i]==t[j])
	      	    {
	      	    i++;
	      	    j++;
				}
			else j=next[j];
			if(j==lt)
			   {
			   printf("%d\n",i-lt+1);
			   j=next[j];
			   cnt++;
		       }
		  }
	return cnt;
}

复杂度分析

时间复杂度： \(O(m+n)\) （听说可以被卡回 \(O(mn)\) ）

空间复杂度： \(O(m)\)

KMP例题

例题 \(1\) ：

P3375 【模板】KMP字符串匹配

KMP板子题，注意匹配成功时的处理，不多赘述。

#include <bits/stdc++.h>
using namespace std;
char s[1000010],t[1000010];
int next1[1000010];
int getnext(char t[],int next[])
{
	int i=0,j=-1,res=-2;
	next[0]=-1;
	int l=strlen(t);
	while(i<l)
	     {
	     	if(j==-1||t[i]==t[j])
	     	   {
	     	   	i++;
	     	   	j++;
	     	   	next[i]=j;
			   }
			else j=next[j];
		 }
	for(int i=0;i<l;i++)
	    res=max(res,next[i]);
	return res;
}

int kmp(char s[],char t[],int next[])
{
	int i=0,j=0,cnt=0;
	int ls=strlen(s),lt=strlen(t);
	while(i<ls)
	      {
	      	if(j==-1||s[i]==t[j])
	      	    {
	      	    i++;
	      	    j++;
				}
			else j=next[j];
			if(j==lt)
			   {
			   printf("%d\n",i-lt+1);
			   j=next[j];
			   cnt++;
		       }
		  }
	return cnt;
}

int main()
{
	scanf("%s",s);
	scanf("%s",t);
	int ans=getnext(t,next1);
	int cnt=kmp(s,t,next1);
	int l=strlen(t);
	for(int i=1;i<=l;i++)
	    printf("%d ",next1[i]);
	return 0;
}

例题 \(2\) ：

P4391 [BOI2009]Radio Transmission 无线传输

此题最大的难点在于如何求出一个周期。

我们可以求出整个字串的最大公共前缀，然后开始分类讨论：

\(1\) ：周期是完整的

最大公共前缀大致是这样：

周期 周期  ... 周期 周期
——————————————————                  (前缀)
     ——————————————————— (与前缀相同的部分)

此时，用字符串总长度减去最大公共前缀的长度就是答案，也就是 \(n-next[n]\) 。

\(2\) ：周期不是完整的

最大公共前缀大致是这样：

半周 周期  ... 周期 半周
——————————————————                  (前缀)
     ——————————————————— (与前缀相同的部分)

把中间的一堆完整周期看作一个周期，因为无论有多少个整周期都没有影响，问题就变成了这样：

半周 周期 半周
————————                 (前缀)
     ———————— (与前缀相同的部分)

由最大公共前缀，得到这两段是完全相同的。所以可以把前面的半周对应到底下的前周，就是这样：

半周 前周 后周 半周
—————————————               (前缀)
     ————————————(与前缀相同的部分)

西周 东周 周天子

所以前面的半周与前周完全相同，就可以把前面的半周都消掉，同理也可以消掉后周，就变成了：

半周 周期  ... 周期 半周
——————————————————                  (前缀)
     ——————————————————— (与前缀相同的部分)

结论还是 \(n-next[n]\) 。

#include <bits/stdc++.h>
using namespace std;
char t[1000010];
int next1[1000010];
int getnext(char t[],int next[])
{
	int i=0,j=-1,res=-2;
	next[0]=-1;
	int l=strlen(t);
	while(i<l)
	     {
	     	if(j==-1||t[i]==t[j])
	     	   {
	     	   	i++;
	     	   	j++;
	     	   	next[i]=j;
			   }
			else j=next[j];
		 }
	for(int i=0;i<l;i++)
	    res=max(res,next[i]);
	return res;
}

int main()
{
	int ans;
	scanf("%d%s",&ans,t);
    getnext(t,next1);
	printf("%d",ans-next1[ans]);
	return 0;
}

例题 \(3\) ：

P8112 [Cnoi2021]符文破译

借用 KMP 思想优化的动态规划。

首先，用 \(dp[i]\) 表示把前 \(i\) 位的字符完全匹配需要的最少词缀数（下标均从 \(1\) 开始）。那么，我们可以从点 \(i+1\) 开始，向后逐位与字符串 \(T\) 比较。设此时匹配到了 \(T\) 中的第 \(j\) 位，如果相等，则易得转移方程：

\[dp[i+j]=\min(dp[i+j],dp[i]+1)
\]

如果不相等或到达了字符串 \(T\) 末尾，则证明在此之后不会更长的有魔法词缀，可以结束这一次匹配，令 \(i=i+1\) 计算下一位即可。

很明显，这个算法的时间复杂度是 \(O(|S||T|)\) 的，当数据范围达到 \(|S|,|T|\le10^6\) 时，算法必然超时。

考虑优化这个算法，我们知道，如果不相等或到达了字符串 \(T\) 末尾，失配后是可以直接跳过一部分不可能产生新的解的数据。这样就自然而然地想到了用这个思想把单模字符串匹配优化到 \(O(|S|+|T|)\) 的 KMP 算法。

借助 KMP 的思想，首先求出字符串 \(T\) 的 \(next\) 数组，然后开始按照 KMP 的方式匹配：（设此时文本串匹配到第 \(i\) 项，模式串匹配到第 \(j\) 项）

设置一个名为 \(now\) 的临时变量，用于存储如果匹配的最少词缀数。

可以直接逐位比较。如果相等，则按照 KMP 思想，将模式串和文本串指针一起后移，令 \(dp[i]=now\) 后比较下一位。

如果不相等，可以令 \(j=next[j]\) 之后重新计算 \(now\) 的值。因为一旦匹配失败，只能再次选择一个词缀。每次 KMP 算法在匹配失败后，会利用最长公共前后缀的性质使得文本串指针 \(i\) 不往前跳。而每次利用最长公共前后缀的性质，会改变模式串匹配的起始位置，所以需要重新计算 \(now\) 的值。可以直接用 \(dp[i-j]\) 计算出模式串匹配的起始位置的前一个位置，把 \(now\) 的值更新为 \(dp[i-j]+1\) 以保证正确性。模式串匹配到末尾也是同理。

DP 边界：\(dp[0]=1\)。

DP 目标：\(dp[|S|]\)。

时间复杂度：\(O(|S|+|T|)\)。

注意，由于有无解的情况，所以当 \(next\) 数组跳到 \(-1\) 时，应该直接判定无解并输出 Fake。因为如果 \(next\) 数组跳到 \(-1\) 证明匹配第一个字符就失配了，此时后面没有办法再进行匹配，无解。

完整代码：（由于代码中的字符串下标是从 \(0\) 开始的，所以可能会和上文的讲解有些出入）

#include <bits/stdc++.h>
using namespace std;
int lt,ls,next1[10000010],f[10000010];
char t[10000010],s[10000010];
void get_next(char t[],int next[])
{
	int i=0,j=-1;
	next[0]=-1;
	while(i<lt)
	   {
	   	if(j==-1||t[i]==t[j])i++,j++,next[i]=j;
	   	else j=next[j];
	   }
}

bool kmp(char s[],char t[],int next[])
{
	int i=0,j=0,now=1;
	f[0]=1;
	while(i<ls)
	   {
	   	if(j==-1)return 0;
	   	if(s[i]==t[j])i++,j++,f[i]=now;
	   	else j=next[j],now=f[i-j]+1;
	   	if(j==lt)now=f[i-j]+1,j=next[j];
	   }
	return 1;
}

int main()
{
	scanf("%d%d%s%s",&lt,&ls,t,s);
	get_next(t,next1);
	if(!kmp(s,t,next1))printf("Fake");
	else printf("%d",f[ls]);
    return 0;
}

后记

为什么只有两道例题？因为别的我不会

UPD on 2024/6/23 现在有三道例题了。

集训真的好累好累啊，眼睛受不了的！

不过能提升我的OI水平，想想也没什么的。