CodeForces 682E Alyona and Triangles （计算几何）

Alyona and Triangles

题目连接：

http://acm.hust.edu.cn/vjudge/contest/121333#problem/J

Description

You are given n points with integer coordinates on the plane. Points are given in a way such that there is no triangle, formed by any three of these n points, which area exceeds S.

Alyona tried to construct a triangle with integer coordinates, which contains all n points and which area doesn't exceed 4S, but, by obvious reason, had no success in that. Please help Alyona construct such triangle. Please note that vertices of resulting triangle are not necessarily chosen from n given points.

Input

In the first line of the input two integers n and S (3 ≤ n ≤ 5000, 1 ≤ S ≤ 1018) are given — the number of points given and the upper bound value of any triangle's area, formed by any three of given n points.

The next n lines describes given points: ith of them consists of two integers xi and yi( - 108 ≤ xi, yi ≤ 108) — coordinates of ith point.

It is guaranteed that there is at least one triple of points not lying on the same line.

Output

Print the coordinates of three points — vertices of a triangle which contains all n points and which area doesn't exceed 4S.

Coordinates of every triangle's vertex should be printed on a separate line, every coordinate pair should be separated by a single space. Coordinates should be an integers not exceeding 109 by absolute value.

It is guaranteed that there is at least one desired triangle. If there is more than one answer, print any of them.

Sample Input

4 1

0 0

1 0

0 1

1 1

Sample Output

-1 0

2 0

0 2

题意：

给出n个点，任意三个点组成的三角形面积不超过S；

构造一个大三角形覆盖上述所有n个点，并且面积不超过4S；

题解：

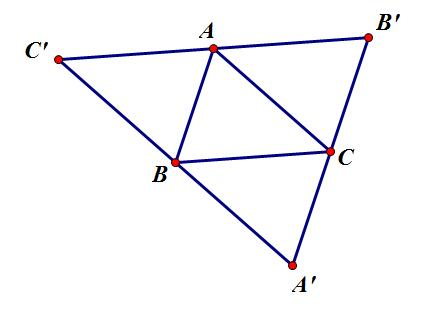
先找出最大的三角形；

再根据性质往三边拓展三个相同的三角形，面积即不超过4S；

找最大三角形：不停遍历n个点加入三角形点集合，可以证明复杂度不超过O(n^2)；

(图盗用自@qscqesze同学~)

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#include <vector>
#define LL long long
#define double LL
#define eps 1e-8
#define maxn 5100
#define mod 1000000007
#define inf 0x3f3f3f3f
#define IN freopen("in.txt","r",stdin);
using namespace std;

struct Point{
    double x,y;
    Point(){}
    Point(double tx,double ty) {x=tx;y=ty;}
}p[maxn];;

double xmul(Point p0,Point p1,Point p2)
{return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);}

double triangle_area(Point a,Point b,Point c) {
    return abs(xmul(a,b,c));
}

int main(void)
{
    //IN;

    int n; LL S;
    while(scanf("%d %I64d", &n,&S) != EOF)
    {
        for(int i=1; i<=n; i++)
            scanf("%I64d %I64d", &p[i].x,&p[i].y);

        bool flag = 1;
        int a=1, b=2, c=3;
        double ans = triangle_area(p[a],p[b],p[c]);
        while(flag) {
            flag = 0;
            for(int i=1; i<=n; i++) {
                double tmp;
                tmp = triangle_area(p[a],p[b],p[i]);
                if(tmp > ans) {
                    ans = tmp; c = i; flag = 1;
                }
                tmp = triangle_area(p[a],p[i],p[c]);
                if(tmp > ans) {
                    ans = tmp; b = i; flag = 1;
                }
                tmp = triangle_area(p[i],p[b],p[c]);
                if(tmp > ans) {
                    ans = tmp; a = i; flag = 1;
                }
            }
        }

        cout << p[a].x+p[b].x-p[c].x << ' ' << p[b].y+p[a].y-p[c].y << endl;
        cout << p[a].x+p[c].x-p[b].x << ' ' << p[c].y+p[a].y-p[b].y << endl;
        cout << p[c].x+p[b].x-p[a].x << ' ' << p[b].y+p[c].y-p[a].y << endl;
    }

    return 0;
}