详解XOR（异或）运算加密

逻辑运算之中，除了 AND 和 OR，还有一种 XOR 运算，中文称为"异或运算"。它的定义是：两个值相同时，返回false，否则返回true。也就是说，XOR可以用来判断两个值是否不同。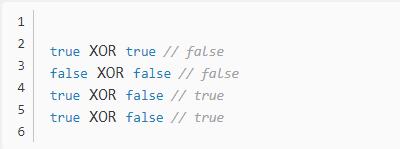


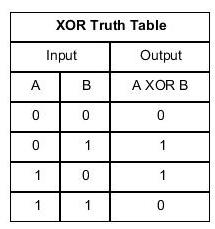
JavaScript 语言的二进制运算，有一个专门的 XOR 运算符，写作^。

如果两个二进制位相同，就返回0，表示false；否则返回1，表示true。

XOR 的应用
XOR 运算有一个很奇妙的特点：如果对一个值连续做两次 XOR，会返回这个值本身。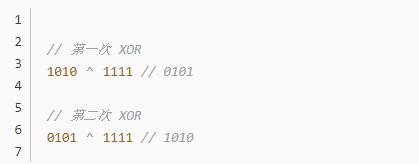

上面代码中，原始值是1010，再任意选择一个值（上例是1111），做两次 XOR，最后总是会得到原始值1010。这在数学上是很容易证明的。

加密应用
XOR 的这个特点，使得它可以用于信息的加密。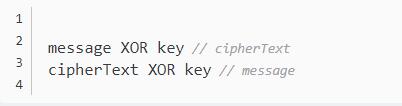

上面代码中，原始信息是message，密钥是key，第一次 XOR 会得到加密文本cipherText。对方拿到以后，再用key做一次 XOR 运算，就会还原得到message。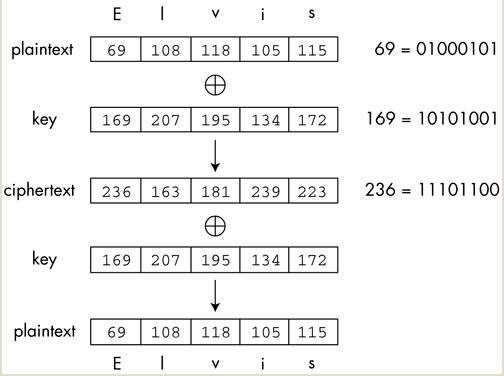

完美保密性
二战期间，各国为了电报加密，对密码学进行了大量的研究和实践，其中就包括 XOR 加密。
战后，美国数学家香农将他的研究成果公开发表，证明了只要满足两个条件，XOR 加密是无法破解的。

key的长度大于等于message
key必须是一次性的，且每次都要随机产生

理由很简单，如果每次的key都是随机的，那么产生的CipherText具有所有可能的值，而且是均匀分布，无法从CipherText看出message的任何特征。也就是说，它具有最大的"信息熵"，因此完全不可能破解。这被称为 XOR 的"完美保密性"（perfect secrecy）。

满足上面两个条件的key，叫做 one-time pad（缩写为OTP），意思是"一次性密码本"，因为以前这样的key都是印刷成密码本，每次使用的时候，必须从其中挑选key。

其中信息熵可以按以下通俗的理解

要理解信息熵，其实并不难，因为生活中无处不是信息熵的体现。比如，假设你是一个伪球迷，对各国家足球队实力一点都不了解，问你冠军赛两支队伍谁可能夺冠。首先经过你脑海的是，这两家国家队可能实力相当，用概率学的说法，即两支球队夺冠的概率都是50%，那么结果就像是掷硬币，正反靠天时地利人和，并无从考证——我们设定这种情景为A。这个时候，有个人跑过来和你说，他是一个足球评论员，对各足球对非常了解，然后告诉你此次冠军赛实力相差悬殊，德国队近来年表现优秀，主帅勒夫策略非凡，而另外一支队伍已经有很多届未进入世界杯总决赛了；基于这些不完整信息，作为伪球迷的你，心理肯定给德国队夺冠加分，假设这个时候你心理的夺冠概率变成了德国队80%的夺冠率，而另一支队伍只剩20%的夺冠率——我们设定这种情景为A+。我们知道，比赛的结果只有一个，冠军也只有一支队伍。结果出来了，有人跑过来准备跟你说到底谁夺冠了，如果你只是在A情境下，这个夺冠信息对你肯定很有诱惑力，因为你本来就无法判断谁可能夺冠；如果你是在A+情境下，这个夺冠信息对你来说多少有点失去新鲜，因为世界级的赛事，出差错的可能性不高，所以你会觉得你其实已经大概知道了结果，听或不听没有太大意义。换种说法表述，晚上冠军赛开战，如果你身处情景A，你肯定比较好奇，势均力敌的双方到底谁能夺冠；而如果你身处情景A+，你会觉得这是一场结果已定的赛事，没有太大兴趣。

好的，举了这么一个例子，你应该已经开始恍然了，信息会改变你对事物的未知度和好奇心，信息量越大，你对事物越了解，进而你对事物的好奇心也会降低，因为你对事物的确定性越高。至此，为了抽象这个模型，聪明的香农总结出了信息熵这个概念。信息熵用以表示一个事物的非确定性，如果该事物的非确定性越高，你的好奇心越重，该事物的信息熵就越高。我们先抛出信息熵的公式
详细了解可以参照 https://blog.csdn.net/wendingzhulu/article/details/42045137