BZOJ 4727: [POI2017]Turysta

4727: [POI2017]Turysta

Time Limit: 20 Sec  Memory Limit: 128 MBSec  Special Judge
Submit: 117  Solved: 39
[Submit][Status][Discuss]

Description

给出一个n个点的有向图，任意两个点之间有且仅一条有向边。对于每个点v，求出从v出发的一条经过点数最多，

且没有重复经过同一个点两次以上的简单路径。

Input

第一行包含一个正整数n(2<=n<=2000)，表示点数。接下来n-1行，其中的第i行有i-1个数，如果第j个数是1，那么

表示有向边j->i+1，如果是0，那么表示有向边j<-i+1。

Output

输出n行，第i行首先包含一个正整数k，表示从i点出发的最优路径所经过的点数，接下来k个正整数，依次表示路

径上的每个点。若有多组最优解，输出任意一组。

Sample Input

4
1
1 1
1 0 1

Sample Output

4 1 2 3 4
3 2 3 4
3 3 4 2
3 4 2 3

HINT

Source

鸣谢Claris上传

分析：

这是一张有向完全图也就是竞赛图...

No.1 竞赛图一定存在一条哈密顿路径

我们可以构法证明，详细证明请移步这里

No.2 强联通的竞赛图一定存在一条哈密顿回路

依旧是构造法证明，构造方法如下：

首先，我们求出这个强联通分量的哈密顿路径，然后把路径变成环，然后考虑扩大环的大小...

把路径变成环就不用说了，一定存在一个环...

然后考虑下面的几种情况：

6代表的是链上离环最近的点

1、存在一条6->1的路径，直接连上就好(这个和第二种情况的区别就是5这个点是环和链的连接点，第二种情况是环上任意点，本质上是一样的，但是代码实现有一些区别...)

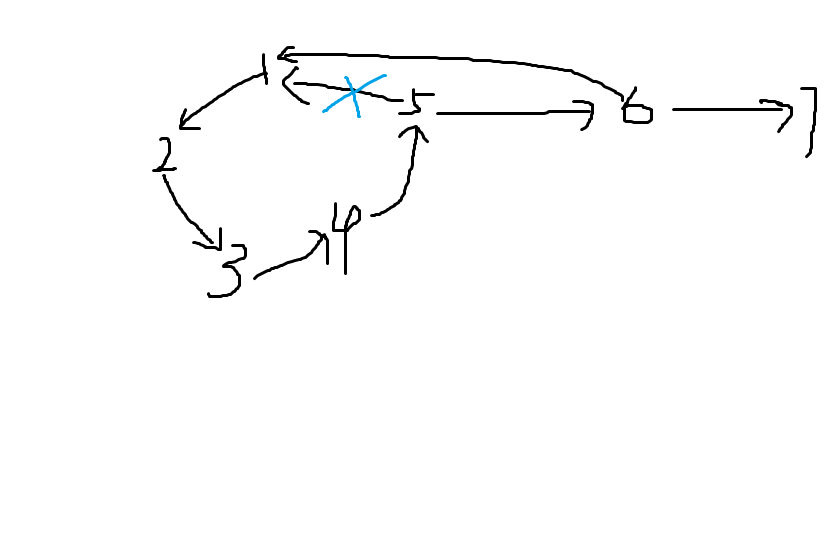
2、存在一条x->6->nxt[x]的路径

3、6不指向环上任何一个点，这时候一定存在链上其他的点指向环上(因为这个图是强联通的)，比如说存在一条7->2的路径，那么新的环就是1->6->7->2->3->4->5->1

这样我们就构造除了一个强联通竞赛图的哈密顿回路...

我们把给出的竞赛图缩点，每个点是一个强联通分量，这就变成了一张DAG，每个强联通分量中找出一个哈密顿回路，那么发现不管从哪个点进入强联通分量都可以遍历这个环然后到达这个强联通分量指向的下一个强联通分量，因为这个强联通分量里的每个点都存在指向下一个强联通分量的边，否则这个和下一个就强联通了...

所以我们DP计算出从这个点出发所能找到的最长的路径...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;

const int maxn=2000+5;

int n,tail,G[maxn][maxn],M[maxn][maxn],ans[maxn],que[maxn],siz[maxn],node[maxn],can[maxn];
int C,tim,top,mp[maxn],dfn[maxn],low[maxn],stk[maxn],vis[maxn],instk[maxn],f[maxn],nt[maxn],nxt[maxn];

inline void push(int x){
	vis[x]=1;
	for(int i=1;i<=tail;i++)
		if(G[que[i]][x])
			can[que[i]]=1;
}

inline void find(void){
	int l=que[1],r=que[1];
	for(int i=2;i<=tail;i++){
		int x=que[i];
		if(G[x][l])
			nxt[x]=l,l=x;
		else{
			for(int now=l,last=0;;last=now,now=nxt[now]){
				if(last==r){
					nxt[r]=x;r=x;
					break;
				}
				else if(G[x][now]){
					nxt[last]=x;
					nxt[x]=now;
					break;
				}
			}
		}
	}
	int d=l;push(l);
	while(d!=r){
		int x=nxt[d];
		if(G[x][l])
			d=x,push(x);
		else{
			for(int now=l,last=0;;last=now,now=nxt[now]){
				if(G[x][now]){
					nxt[last]=x;
					nxt[d]=l;
					d=x;l=now;
					push(x);
					break;
				}
				else if(last==d){
					int nownode,t;
					for(int i=1;i<=tail;i++)
						if(!vis[que[i]]&&can[que[i]]){
							nownode=que[i];
							break;
						}
					for(int i=l;;i=nxt[i])
						if(G[nownode][i]||i==d){
							t=i;
							break;
						}
					for(int i=nxt[d];;i=nxt[i]){
						push(i);
						if(i==nownode)
							break;
					}
					nxt[d]=l,l=t,d=nownode;
					for(int now=l;;now=nxt[now])
						if(nxt[now]==t){
							nxt[now]=x;
							break;
						}
					break;
				}
			}
		}
	}
	nxt[r]=l;
	for(int i=1;i<=tail;i++)
		vis[que[i]]=can[que[i]]=0;
}

inline void tarjan(int root){
	dfn[root]=low[root]=++tim,stk[++top]=root,instk[root]=1;
	for(int i=1;i<=n;i++)
		if(G[root][i]){
			if(!dfn[i])
				tarjan(i),low[root]=min(low[root],low[i]);
			else if(instk[i])
				low[root]=min(low[root],dfn[i]);
		}
	if(dfn[root]==low[root]){
		C++;node[C]=root;tail=0;int tmp;
		do{
			tmp=stk[top--];instk[tmp]=0;mp[tmp]=C;siz[C]++;que[++tail]=tmp;
		}while(tmp!=root);
		find();
	}
}

inline int dp(int x){
	if(f[x])
		return f[x];
	for(int i=1,tmp;i<=C;i++)
		if(i!=x&&M[x][i]){
			tmp=dp(i);
			if(f[x]<tmp)
				f[x]=tmp,nt[x]=i;
		}
	f[x]+=siz[x];
	return f[x];
}

inline void print(int x){
	if(x){
		printf(" %d",x);
		for(int i=nxt[x];i!=x;i=nxt[i])
			printf(" %d",i);
		print(node[nt[mp[x]]]);
	}
}

signed main(void){
	scanf("%d",&n);
	for(int j=2;j<=n;j++)
		for(int i=1;i<j;i++)
			scanf("%d",&G[i][j]),G[j][i]=G[i][j]^1;
	for(int i=1;i<=n;i++)
		if(!dfn[i])
			tarjan(i);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(G[i][j]&&mp[i]!=mp[j])
				M[mp[i]][mp[j]]=1;
	for(int i=1;i<=C;i++)
		dp(i);
	for(int i=1;i<=n;i++)
		printf("%d",f[mp[i]]),print(i),puts("");
	return 0;
}

　　

---

By NeighThorn