Treap讲解

Treap讲解

　　上一篇blog提出了Treap这个算法，在这里我就要详细讲解。

　　首先，我们可以从字面上理解这个算法，Treap这个单词是由Tree和Heap两个单词构成的，所以它的性质就很好理解了，明显就是同时满足Tree和Heap两个算法的性质，那么Tree是什么呢？

Heap又是什么呢？Tree是BST，而Heap是堆，如果这两个算法不懂的话可以先学习一下，因为Treap是在这两个算法的基础上产生的，BST可以看我的上一篇博客，而Heap就只能再找了，本人比较懒，没有写，见谅。

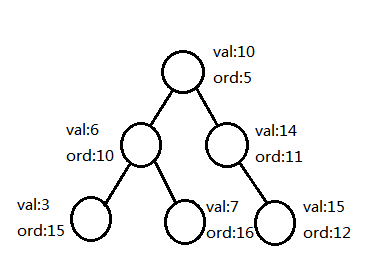
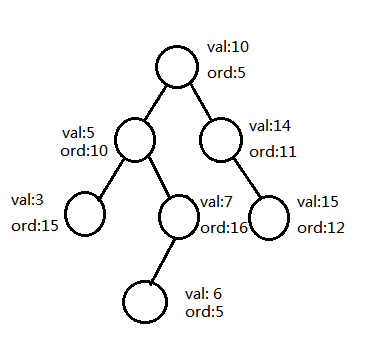
　　好了言归正传，如何将BST的性质和Heap的性质结合在一起呢？似乎比较简单，我们可以在BST的基础上再开一个数组，来进行维护堆的性质，这个数组我们可以随意赋值，但是整体的数需要满足堆的性质（如左下图）。在图中的树就明显满足，val的排序方式是按照BST，而ord的排序方式是按照小根堆。这样的性质就十分靠谱，因为我每次堆ord的赋值是随机的，所以不论插入的顺序是什么，我们都可以完美的解决危机。现在问题来了，插入时找到节点了，也赋完值了，但是突然发现不满足Heap的性质了（如右下图），怎么办？

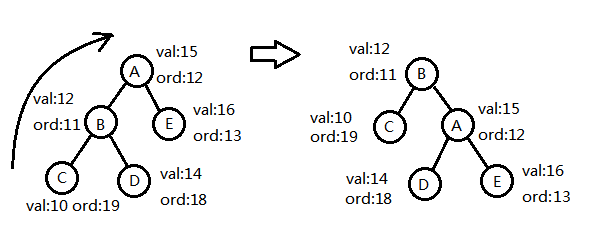
　　这个时候，我们就可以引出Treap的核心部分，左旋和右旋。首先讲右旋，当当前节点的左儿子的ord小于自己的时候，我们可以进行这个操作，如下图，经过这样一个小小的变换，性质就有满足了，这个转换比较好实现，我们可以直接对节点的儿子编号进行修改还就好了。

 void rturn(int &p)
 {
     int tmp=lson[p];
     lson[p]=rson[tmp],rson[tmp]=p;
     p=tmp;
 }
 //lson[p]记录p号节点的左儿子的编号
 //rson[p]记录p号节点的右儿子的编号

右旋

 void lturn(int &p)
 {
     int tmp=rson[p];
     rson[p]=lson[tmp],lson[tmp]=p;
     p=tmp;
 }
 //lson[p]记录p号节点的左儿子的编号
 //rson[p]记录p号节点的右儿子的编号

左旋

　　这是两个基本操作，只要写treap就需要用到。下面讲解一下基本操作：添加，单点删除。

　　添加：添加操作比较简单，首先找到只满足BST性质的位置，将其添加进Treap中，如果这是一个新节点，我们可以在上面赋值ord，这是一个随机的数值，之后就可以回溯了。当每一次回溯的时候，我们需要判断一下，是否需要左旋或者右旋，即可，是不是很简单？

 void add(int &p,int number)
 {
     if(!p)
     {
         p=++idx,ct[p]=,val[p]=number;
         size[p]=,ord[p]=rand();
         return;
     }
     size[p]++;
     if(val[p]==number) ct[p]++;
     else if(np<number)
         add(rson[p],number);
     else if(np>number)
         add(lson[p],number);
     if(ord[rson[p]]<ord[p]) lturn(p);
     if(ord[lson[p]]<ord[p]) rturn(p);
 }
 //ct[p]记录p号节点出现的次数
 //lson[p]记录p号节点的左儿子的编号
 //rson[p]记录p号节点的右儿子的编号
 //val[p]记录p号节点的权值
 //ord[p]记录p号节点的随机值
 //size[p]记录以p号节点为根的子树的大小
 //number是要插入的权值

添加

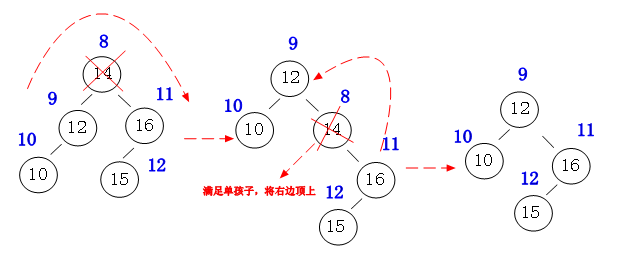
　　单点删除：我们首先需要查询到当前点，如果当前点的ct>1，我们可以直接ct--，如果不是，我们需要把它旋到最下面，每一次旋转都是把自己的左儿子和右儿子中ord小的点旋上来，直到把要删除的节点旋到最下面为止，直接删去它和它父亲的连边就好了。当然，有时候会出现一种情况，就是旋到当前节点只有左儿子或者右儿子，直接把当前节点的儿子提上来就好了（如图）（注：这张图片来自http://www.cnblogs.com/huangxincheng/archive/2012/07/30/2614484.html，本人较懒，就不用画图画了）

 void del(int &p,int number)
 {
     if(!p) return;
     if(val[p]==number)
     {
         if(ct[p]>)
         {
             ct[p]--,size[p]--;
             return;
         }
         if(lson[p]*rson[p]==) p=lson[p]+rson[p];
         else if(ord[lson[p]]<ord[rson[p]])
             rturn(p),del(p,number);
         else if(ord[rson[p]]<=ord[lson[p]])
             lturn(p),del(p,number);
         return;
     }
     size[p]--;
     if(val[p]<number)
         del(rson[p],number);
     else del(lson[p],number);
 }
 //ct[p]记录p号节点出现的次数
 //lson[p]记录p号节点的左儿子的编号
 //rson[p]记录p号节点的右儿子的编号
 //val[p]记录p号节点的权值
 //ord[p]记录p号节点的随机值
 //size[p]记录以p号节点为根的子树的大小
 //number是要插入的权值

删除

大致就是这样，不会的可以评论发问题，我会解答。